接上文；上文(CFL-Reachability求解Andersen指针分析)主要介绍了将Andersen式指针分析问题转换为CFL-Reachability问题，然后进行求解。本文介绍介绍另一篇Andersen式指针分析，作者提出的方法是字段敏感的。

我看这篇文章的动机是：

• 它被用在GCC编译器的指针分析中，Go语言指针分析中
• 我觉得这篇文章里面讲的一些求解方法很经典
• C的字段敏感指针分析我看得并不多

这篇文章最初发表在PASTE’04，在2007年又以一个更详细的版本发表在TOPLAS’07。

作者提出的方法对结构体变量和间接函数调用进行建模。它是流不敏感，上下文不敏感，字段敏感的。

1. 集合约束式的指针分析

1.1 基本介绍

Set-Constraints指针分析，也叫Andersen式指针分析，inclusion-based指针分析。约束可以用如下形式来描述：

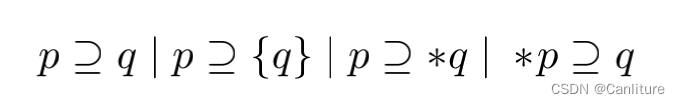
在对程序进行分析时，根据程序的语意，收集相应的约束，表示成上述所示的约束

• 程序中每个变量，都有一个唯一的约束变量与之对应
• 每个变量都包含一个集合，表示它所指向的位置
• 程序的赋值也转换成上述的约束形式

得到约束之后，能够通过如下所示的推导规则来得到每个变量最终的指向状态。

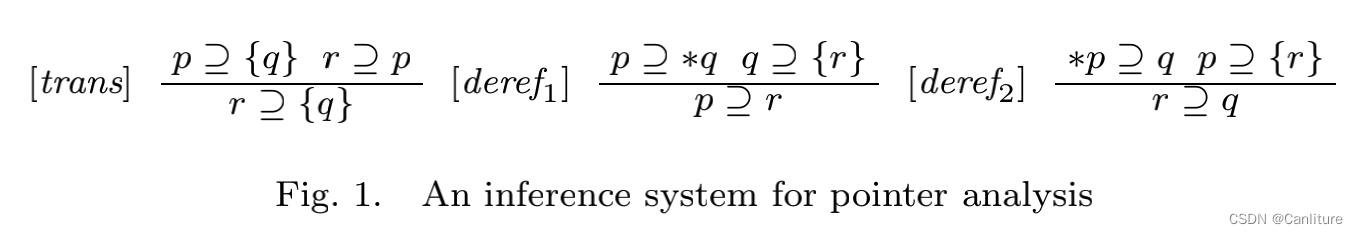
看起来比较简洁。这里以一个例子为描述：

• (1) ~ (7)：根据程序的语意来收集的约束关系。
  • 约束变量以函数名 + 变量名下标来唯一表示
• (8) ~ (13)：根据推导规则，得到进一步的约束关系

1.2 求解约束

给定一个程序，然后构造了上述约束，如何进行求解，得到变量最终的指向状态？

首先，给出求解时间，再给出求解方法。

约束系统中存在 t 个约束，它能够以 $O(t^3)$ 时间进行求解

证明：

• v是变量数目，那么生成的简单约束 ($p \supseteq {q} $) 的上界数为 $O(v^2)$
• 最多 $O(v^2)$ 种简单约束可能性 ( $p\supseteq q$ )
• 最多有v个简单约束能够通过trans规则在每个简单约束之间传播，应用trans最多 $O(v^3)$ 次。
• 每个解引用的变量最多 $O(v)$ 个targets，复杂约束规则只能应用 $O(tv)$ 次
• v就是O(t)，所以 $O(t^3)$ 上界

作者提到：他提出的字段敏感算法是 $O(v^4)$

这里讨论一些高效求解约束的方法。

当然，最简单的方法就是用一个 while(changed) 循环盲目地迭代，直到不动点。

1.2.1 图传播

核心思想就是将约束表示成有向图。

• 每个约束变量表示成图上唯一的节点
• $p\supseteq q$ 表示成图上 $p\leftarrow q$ 边

每个节点关联一个解(points-to set)的集合，叫做 $Sol(n)$

例如之前的例子可以用下图来表示：

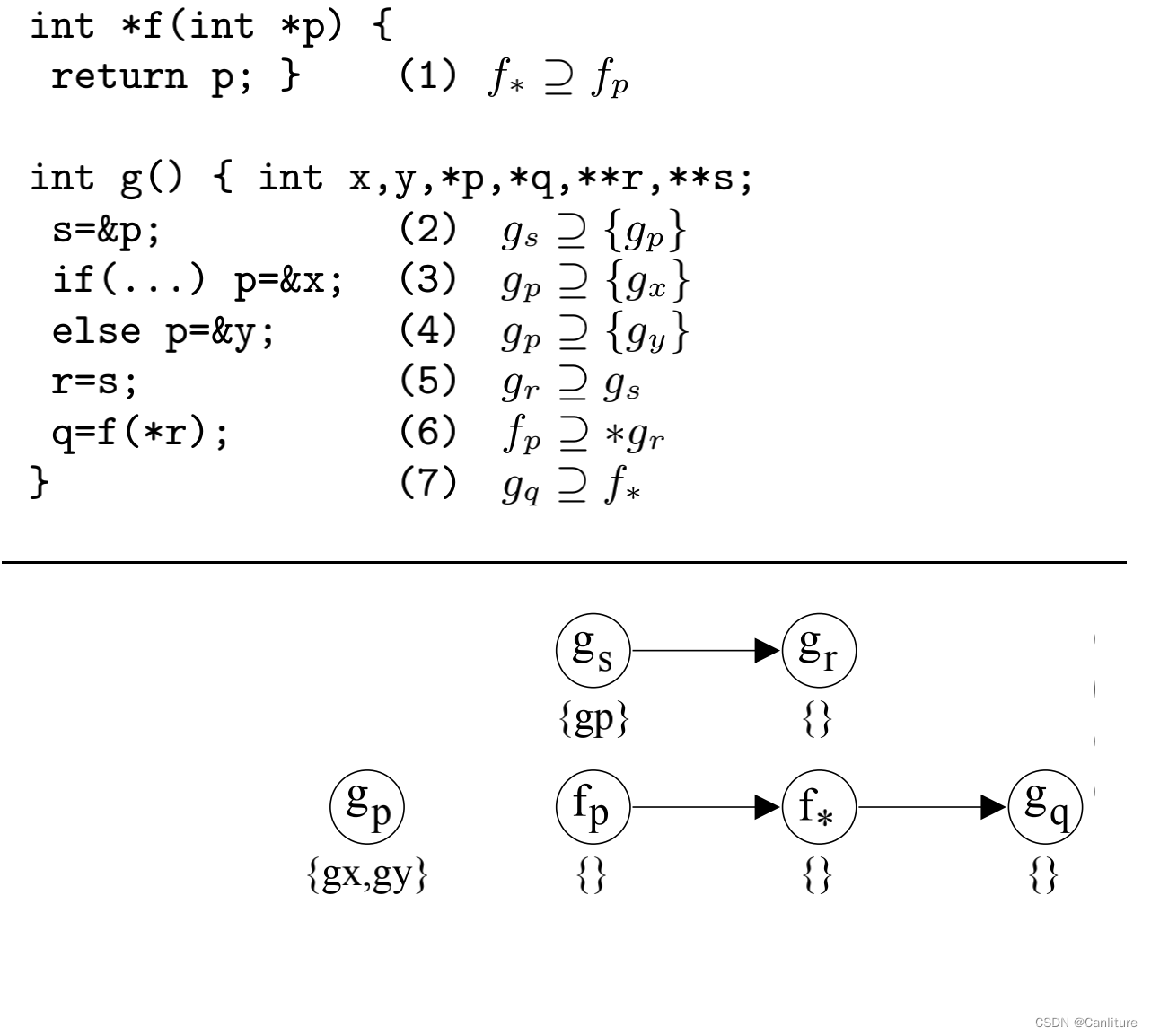
图的最初状态只处理这种规则 n ⊇ { x } n \supseteq \{x\} n⊇{x} 。通过worklist算法，不断沿着边传递 $Sol(n)$ 到后继节点。最终得到的解为：

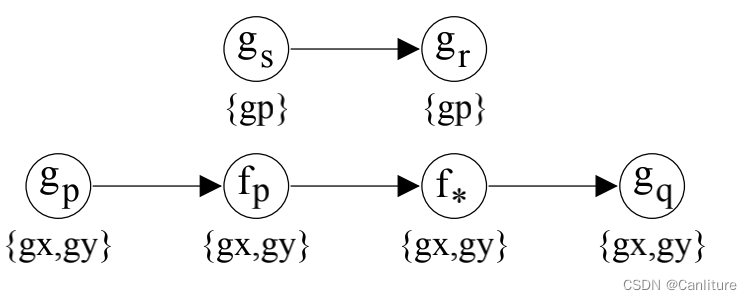
worklist处理细节：$\ast n\supseteq q$：$\forall v \in Sol(n), 添加边v \leftarrow q $ ；其它情况类似的处理方式。

1.2.2 迭代顺序

节点被访问的顺序 (从worklist中拎出来的顺序)，会影响迭代效率。

例如，对于如下状态：

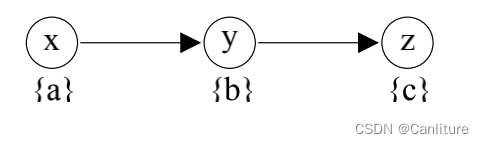
如果我们从worklist中挑出节点y进行迭代传播，就像这样：

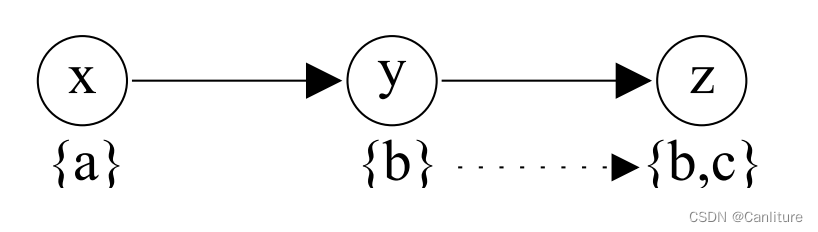
现在再挑出节点x进行传播，很显然，会重新传播y节点的值。 如果一开始就挑出x进行传播，那么显然传播的次数少一些。

1.2.3 节点替换 (Variable Subsititution)

观察到，如果一些变量一定有相同的解，那么，可以将它替换成一个节点，这样就降低图的大小，减少传播次数。

第一种情况如下，{x, y, z} 可以用单个节点替换。

• 关键的思想就是y，z没有被取地址，并且没有这样的形式 $y\supseteq \ast p$
  

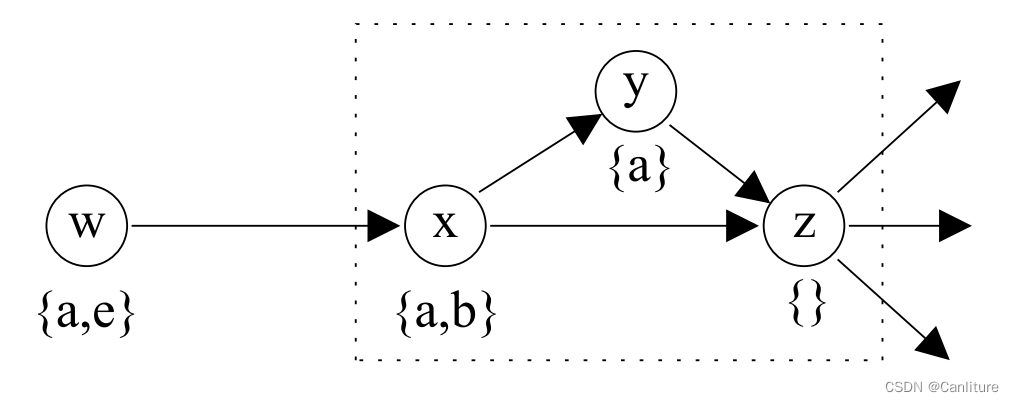
第二种情况就是强连通分量 (Strongly Connected Component)。

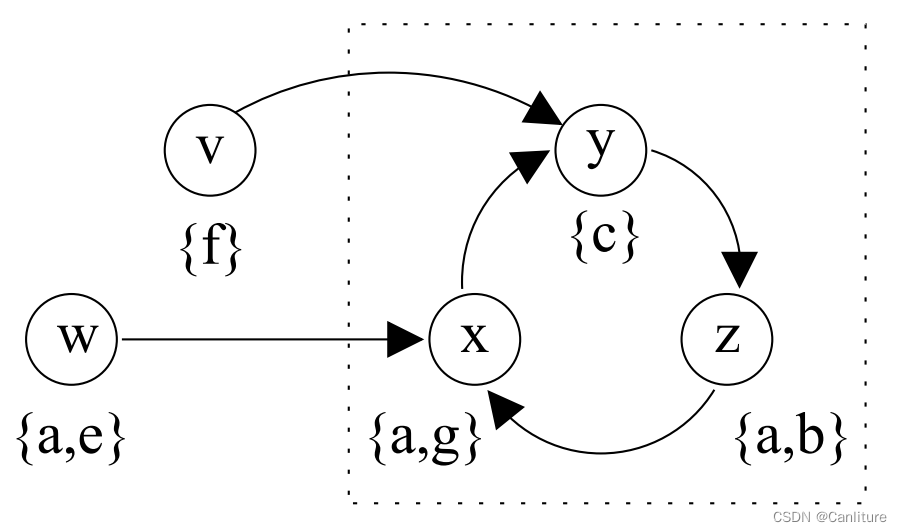
1.2.4 传递化简 (Transitive Reduction)

从图上消除传递边，$x\to z$ 可以消除，但是并不会影响最终解，而且还能够提升性能（执行更少的并集操作）。

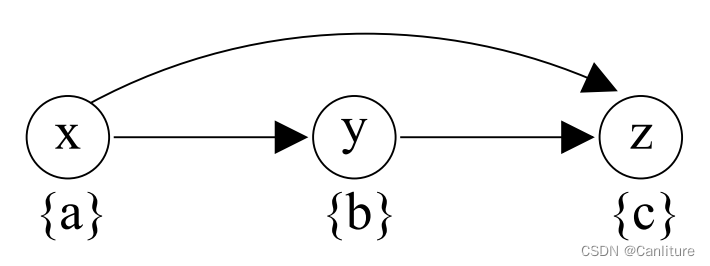
并没有高效地方法来识别这种可化简的传递边( 已有方法是$O(n^2)$ )。但是能够识别一些这样的边，仍然很有用。

1.2.5 集合的表示

一般集合会实现成BitVector，Sorted Array，Binary Tree。最好的实现是BitVector混合Sorted Array方法。

1.2.6 差分传播

可参考南京大学软件分析中指针分析算法，里面也提到了 $\Delta$ 传播

Difffference propagation的意思就是只传播改变的那部分集合到后继节点，这样能够避免重新传播冗余的信息。

构造一个$\Delta = {d} $ ，而非传播整个集合过去。 （作者说BitVector表示并不会加速）

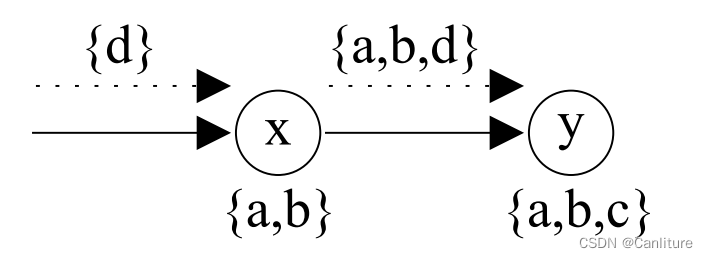
1.2.7 相同解的集合

很多时候迭代到后面，许多变量拥有相同解，作者发现，一般情况下，如果能把相同的集合用哈希表共享，那么能够节约内存，提升求解器整体的执行时间。

2. 扩展约束模型

2.1 简介

上面的约束模型只能够处理简单的变量，以及解引用。这里扩展到函数间接调用 (函数指针)，字段敏感

扩展后的约束，用如下形式来表示：

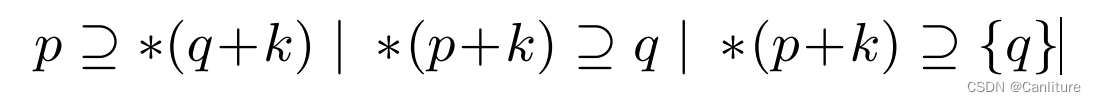
简单解释：

• k为常数
  • 当k=0时，与原来的模型是等效的
• *(p + k)表示：$\forall s\in Sol(q),然后\ast (s+k)$

对应的推导规则如下：

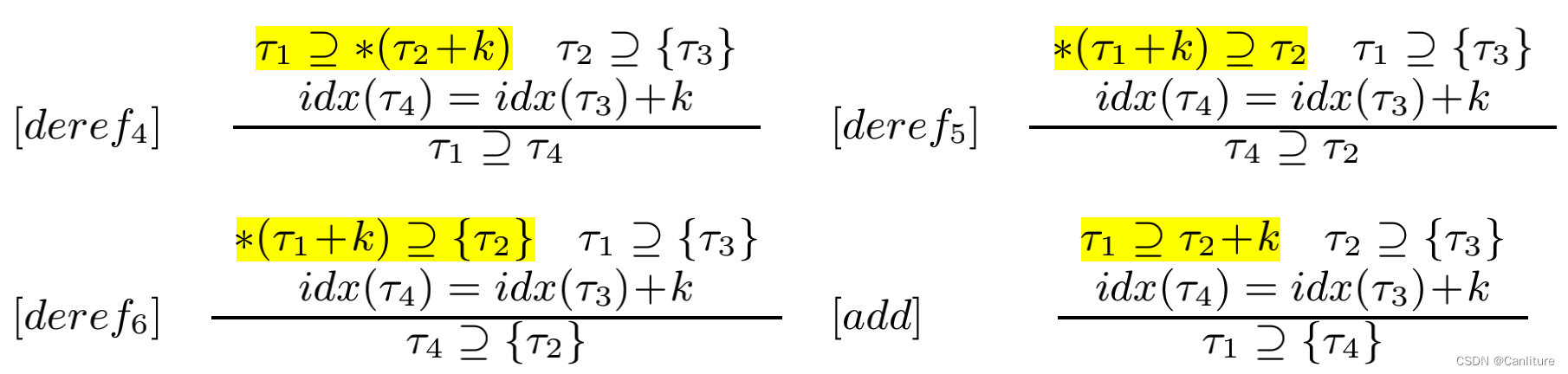
其中

• idx为：映射变量到它的索引
• add规则用于处理这种情况：$q=\&(b->f2)$

用图形表示这种约束关系，可以用带权图（边上标注k值）

• $p\supseteq q+k$ ，引入边 $q\to p,边上权值k$

2.2 处理函数指针

对于函数指针，将函数的第一个参数的索引 (第一个参数的索引) 作为它的索引。

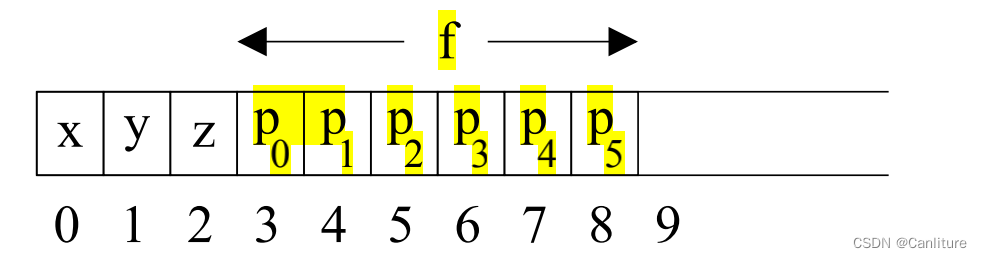
这里是一个例子，主要关注于：

• (1). 函数f的第一个参数p的index为0
• (8). 处理函数的关键就是将函数的index视为该函数第一个参数的index
• (10)(11). 上下文不敏感

这样处理仍然会存在一个问题，就是不合理的类型转换，例如如下代码：

在处理最后一条约束时，会导致 $g_a\supseteq b$ ，因为 $idx(g_a)=idx(f_p)+1$。通过对每个变量限制它的端点(end)索引，可以避免不想要的传播。每个变量有一个end，$end(f_p)=0,end(g_a)=end(g_b)=2$，所以对于 $idx(\ast (g_p+1))>end(\ast g_p)$ 这种情况，可以不做传播。

2.3 处理字段

与Java相比，Java不允许取字段的地址。

有3种方法来处理字段：field-insensitive, field-based, field-sensitive。他们的区别是：

下面看作者怎么对字段建模的：

看起来很容易理解，就是给结构体每个字段变量编个号。

存在的一个问题就是 Positive Weight Cycle (PWC) 问题。这种环会导致求解时不终止，也就是不断地+1，+1 传播…

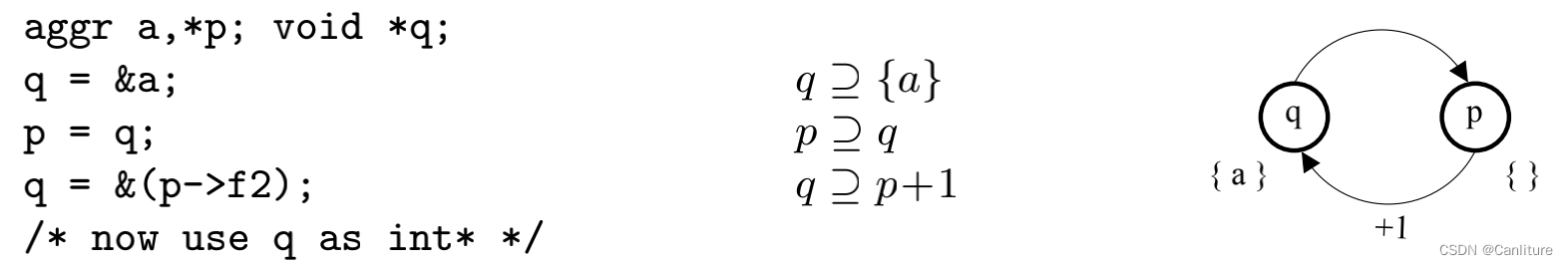
可以使用上文所说的end，来限制自增后的边界索引。

另外就是折叠环。如果所有节点间都存在一条0权路径。那么能够折叠成一个自环节点。

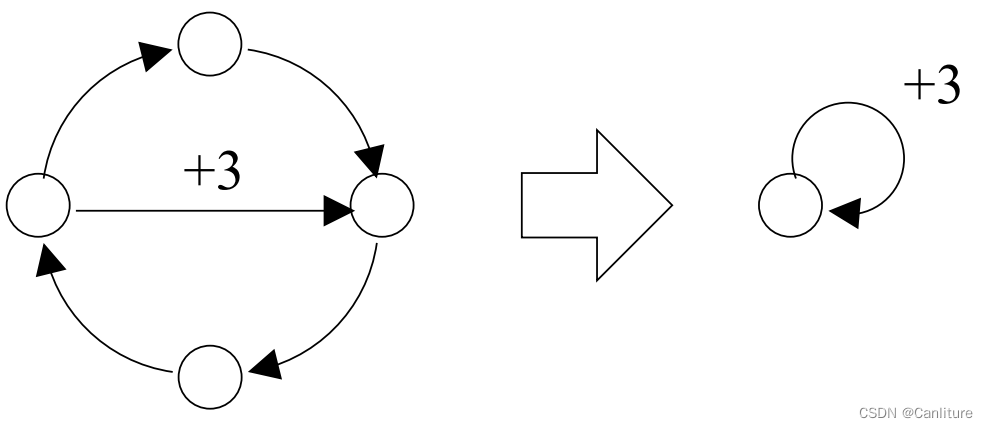
2.4 处理堆

上面提到，对于结构体，就是给结构体里面的字段变量编个号。但是对于堆内存分配，下面给了一个例子：

HEAP0既可以表示结构体，又可以表示整数数组。所以上述给字段编号的方法似乎并不适用，因为我们不知道它到底分配出来被用作结构体还是其它类型的数据。

所以我们要么对这种堆，字段不敏感。要么假设它总是结构体。那么问题来了？程序中声明了这么多结构体，堆变量到底是哪个结构体呢？最简单的方法就是：假定堆变量就是程序中最大的那个结构体，每个堆变量就被认为是所有结构体的union。

2.5 处理指针算数和数组

对于指针算数； $p=p+1$ 你可能会套用这个约束 $p\supseteq p+1$ ，但实际上，我们只对显式的字段访问建模（x->y, x.y这种）。指针算数我们翻译为 $p\supseteq p$

对于数组，看成单个约束变量。

3. 算法