题目描述

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。
示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：“bb”

解题思路

最近在学习左成云大神的动态规划解题思路：暴力递归—>记忆化搜索–>动态规划。对于不容易直接推导出动态规划状态转移方程的题，通过暴力递归尝试到最终的动态规划，理解起来比较清晰，尤其是状态方程的转移过程。

暴力递归

对于回文子串其有一个性质，如果一个字符串S是回文串，那么将S的首尾两个字母去掉剩下的字符串任然是一个回文串
可以通过递归的方式判断一个字符串是不是回文串。定义递归方程process(char[] str, int L, int R)：如果str[L，R]是一个回文串，返回true，否则返回false，
递归终止条件
1. 如果L==R，只有一个字符，一定是回文串，返回true
2. 如果R-1==L，有两个字符
  1. 如果str[L] == str[R]，则这两个字符串一定是回文串，返回true
  2. 否则false

/**
 * @param str
 * @param L 左边界
 * @param R 有边界
 * @return 判断str[L,R]是否为一个回文串
 */
public static boolean process(char[] str, int L, int R) {
    if (L == R) {
        return true;
    }
    if (R - 1 == L) {
        return str[L] == str[R];
    }

    if (process(str, L + 1, R - 1)) {//如果str[L+1,R-1]是一个回文串
        if (str[L] == str[R]) {//首尾两个字符相等，显然str[L,R]也是一个回文串
            return true;
        } else {
            return false;
        }
    } else {//str[L+1,R-1]不是一个回文串，那么str[L,R]更不是一个回文串
        return false;
    }
}

通过上述的递归方程，可以求出所有的str所有的字串是否是一个回文串，接下来可以通过记忆化搜索将所有的字串是否为回文串记录下来

记忆化搜索

记忆化搜索主要是用来优化递归过程的，如果有大量的重复过程，通过数组保存已经计算过的递归过程，下次在遇到该递归过程，可以直接返回记录下的值
对于递归函数process(char[] str, int L, int R)，三个参数只有L和R两个是变化的，所有可以通过一个二维数组dp[L][R]来记录本次递归的返回值
即dp[L][R]=process(char[] str, int L, int R)

dp的初始值
dp数组的初始值可由递归终止条件得出
1. 如果L==R，只有一个字符，一定是回文串，返回true
  即dp[L][L]= true，
2. 如果R-1==L，有两个字符
  1. 如果str[L] == str[R]，则这两个字符串一定是回文串，返回true
    即dp[L][R+1] = true
  2. 否则false
    即dp[L][R+1]=false
    代码实现如下:
```
int N = str.length;
boolean dp[][] = new boolean[N][N];
dp[N - 1][N - 1] = true;
for (int i = 0; i <= N - 2; i++) {
    dp[i][i] = true;
    dp[i][i+1]=str[i]==str[i+1];
}
```
以字符串str="babad"为例：dp数组的初始值为下图标出的两条对角线:

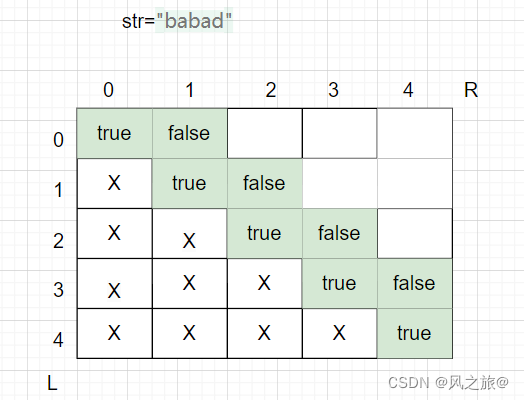
有了初始值，就可以推导出dp数组的状态转移，状态转移过程由递归函数得出

if (process(str, L + 1, R - 1)) {
    if (str[L] == str[R]) {
        return true;
    } else {
        return false;
    }
} else {
    return false;
}

由上述代码可知，从process(str,L,R)会进入process(str,L+1,R-1)中，其中process(str, L + 1, R - 1)可以用dp[L+1][R-1]表示，即dp[L][R]依赖于dp[L+1][R-1]

if (dp[L + 1][R - 1]) {
    if (str[L] == str[R]) {
        dp[L][R] = true;
    } else {
        dp[L][R] = false;
    }
}else {
    dp[L][R]=false;
}
return dp[L][R]

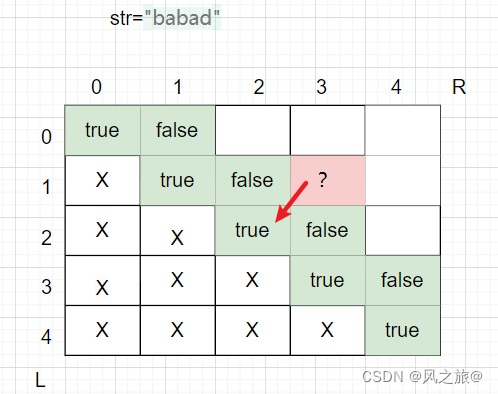
在这里插入图片描述
即问号处的值依赖于左下角箭头指向的值，所有如果想要得出所有的dp数组值，可以从最下面一行从左到右，然后再从上面一行从左到右依次填dp数组，一直到第一行，就可以得出所有的值

动态规划求解

通过上述可以得出所有dp数组值，也就知道了str的所有字串str[L,R]是否为回文串，最后记录最长的回文子串即可
AC代码

public class Solution {
  public static String longestPalindrome(String s) {
        char[] str = s.toCharArray();
        int N = str.length;
        boolean dp[][] = new boolean[N][N];
        int Left = 0;//最长字串的左边界
        int maxLength =1;//最长字串的长度
        //初始值
		dp[N - 1][N - 1] = true;
        for (int i = 0; i <= N - 2; i++) {
            dp[i][i] = true;
            if (str[i] == str[i+1]){
                if (maxLength<2){
                    Left = i;
                    maxLength = 2;
                }
                dp[i][i + 1] = true;
            }else {
                dp[i][i+1]=false;
            }
        }	
        int maxTem;
        //从下往上，从左往右推
        for (int L = N - 3; L >= 0; L--) {
            for (int R = L+2;R<N;R++){
                if (dp[L+1][R-1]){
                    if (str[L]== str[R]){
                        dp[L][R]=true;//是回文串
                        maxTem = R-L+1;//回文串的长度
                        if (maxLength<maxTem){
                            Left = L;
                            maxLength = maxTem;
                        }
                    }else {
                        dp[L][R] = false;
                    }
                }else {
                    dp[L][R] = false;
                }
            }
        }
        return new String(str,Left,maxLength);
    }
}