一、组合数——卢卡斯定理

1、问题

这道题中，$a,b$的范围都是很大的，我们就无法直接用到之前所讲解的预处理阶乘的方法。

如果大家没有看过作者写的组合数（1）的话，建议大家先去看一下，今天所讲的问题需要上一篇文章的铺垫，传送门：组合数（1）

而此时就需要用到我们后文介绍的卢卡斯定理了。

2、卢卡斯定理

（1）定理内容

$$C_a^b=C_{a/p}^{b/p}\ast C_{amod(p)}^{bmod(p)}$$

（2）定理证明

在证明这个算法之前，我们先证明几个小的结论做铺垫。

结论1：

当$0<x<p$的时候：
$$C_p^x\equiv 0mod(p)$$

这个很好证明
$$C_p^x=\frac{p!}{x!(p-x)!}=\frac{p(p-1)!}{x(x-1)!(p-x)!}=\frac{p}{x}\ast C_{p-1}^{x-1}$$

所以$C_p^x$是$p$的倍数。所以$C_p^x\equiv 0mod(p)$

结论2：

$$(1+x{)}^p\equiv 1+x^p(modp)$$

证明：
根据二项展开式：

$(1+x{)}^p=C_p^0{x}^0+C_p^1{x}^1+C_p^2{x}^2+...+C_p^p{x}^p$

根据我们的结论1
我们中间的项在模p的时候，都等于0。

因此，我们可以化简一下就会得到我们的结论2：

$$(1+x{)}^p\equiv 1+x^p(modp)$$

卢卡斯定理证明：

令$a=np+d,b=mp+d$

根据二项展开式：
$(1+x{)}^a\equiv {\sum }_{i=0}^a{C}_a^i{x}^i(modp)$

我们将$a=np+d$带入：

$(1+x{)}^a$
$\equiv (1+x{)}^{np+d}$
$\equiv ((1+x{)}^p{)}^n(1+x{)}^d$

根据结论2，我们可以继续化简得：

$\equiv (1+x^p{)}^n(1+x{)}^d$

再根据二项式展开：

$\equiv {\sum }_{i=0}^n{C}_n^i{x}^{ip}\ast {\sum }_{j=0}^d{C}_d^j{x}^j(modp)$

所以我们就能得到：
$$\sum _{i=0}^a{C}_a^i{x}^i\equiv \sum _{i=0}^n{C}_n^i{x}^{ip}\ast \sum _{j=0}^d{C}_d^j{x}^j(modp)$$

左式和右式中，一一对应，我们可以得到如下结果：

对于任何一项：$x^e$

$$C_a^b{x}^b=C_n^x\ast C_d^y{x}^b$$

其中：$b=x\ast p+y$并且$a=np+d$

即：
$$C_a^b\equiv C_n^x\ast C_d^y$$

而：

$$\begin{gathered} x=\frac{b}{p} \\ n=\frac{a}{p} \end{gathered}$$

$$\begin{gathered} y=bmodp \\ d=amodp \end{gathered}$$

我们将其带入即可得到：
$$C_a^b=C_{a/p}^{b/p}\ast C_{amod(p)}^{bmod(p)}$$

上述式子即我们的卢卡斯定理。

3、代码

#include<iostream>
using namespace std;
typedef long long ll;
int n;
ll qmi(ll a,ll b,ll p)
{
    ll res=1;
    while(b)
    {
        if(b&1)res=res%p*a%p;
        a=a%p*a%p;
        b>>=1;
    }
    return res;
}
ll c(ll a,ll b, ll p)
{
    if(b>a)return 0;
    ll res=1;
    for(int i=1,j=a;i<=b;i++,j--)
    {
        res=res%p*j%p;
        res=res%p*qmi(i,p-2,p)%p;
    }
    return res;
}
ll lucas(ll a,ll b,ll p)
{
    if(a<p&&b<p)return c(a,b,p);
    else return c(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main()
{
    cin>>n;
    while(n--)
    {
        ll a,b,p;
        cin>>a>>b>>p;
        cout<<lucas(a,b,p)<<endl;
    }
}

这里解释一下我们的中间计算$C_a^b$的代码：

我们这里用到了另一个定义：

$$C_a^b=\frac{A_a^b}{A_b^b}=\frac{a(a-1)...(a-b+1)}{b(b-1)(b-2)...1}$$

二、组合数——高精度+欧拉筛

1、问题：

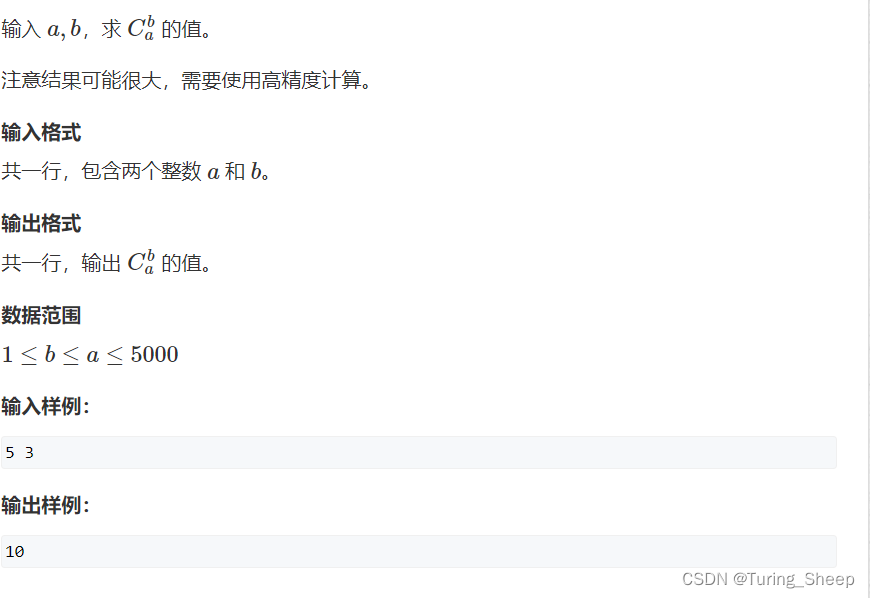
这道题的关键就在于题目给出的$a$和$b$实在是太大了，肯定会爆掉。所以我们要使用高精度算法。

2、思路

这道题的难点就是会爆掉，所以我们要用到最开始学习的高精度算法。然后利用定义求解。

我们先来回顾一下组合数的定义：

$$C_n^m=\frac{n!}{m!(n-m)!}$$

如果我们直接套用高精度算法的话，肯定是相当麻烦的。

所以我们将其变形一下：

根据算数基本定理，我们能够将$C_n^m$写成有限个质数乘积的形式。

那么问题来了，我们如何拆解呢？

首先，拆解质数的关键，在于我们要知道可能包含哪些质数。由于我们的$n\ge m$。所以我们只需要去筛选$1-n$之间所有的质数即可。

而筛选质数的话，我们可以选择之前学过的埃氏筛法或者欧拉筛法。我们此处就选择欧拉筛法了。

当我们知道了包含的质数之后，我们还要计算的是$C_n^m$中所含质数的个数。

那么此时我们将用到下面这个结论：

$$\begin{gathered} n!中p的个数： \\ sum=\frac{n}{p}+\frac{n}{p^2}+\frac{n}{p^3}+.... \end{gathered}$$

为什么呢？
如果我们的阶乘中含有一个$p^k$的倍数。那么此时这个数应该包含$k$个$p$。

如果假设$k>1$的话，

那么他必定是$p$的个数，此时它会被取出来一次。

同时，如果$k>2$的话，

那么它也必定是$p^2$的个数，此时它会被取出来一次。

那么以此类推，它就会被取出来$k$次，也就是说它会被计算$k$次。恰好验证了我们的公式。

当我计算出了质数和对应的指数的时候，我们只需要套用一下高精度乘法，乘在一起即可。

3、代码

#include<iostream>
#include<vector>
using namespace std;
const int N=5e3+10;
int primes[N],cnt;
int sum[N];
bool st[N];
void get_primes(int a)
{
    for(int i=2;i<=a;i++)
    {
        if(!st[i])primes[cnt++]=i;
        for(int j=0;primes[j]<=a/i;j++)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)break;
        }
    }
}
int get_nums(int a,int pri)
{
    int res=0;
    while(a)
    {
        res+=a/pri;
        a/=pri;
    }
    return res;
}
vector<int>mul(vector<int>a,int b)
{
    vector<int>c;
    int t=0;
    for(int i=0;i<a.size();i++)
    {
        t+=a[i]*b;
        c.push_back(t%10);
        t/=10;
    }
    while(t)
    {
        c.push_back(t%10);
        t/=10;
    }
    return c;
}

int main()
{
    int a,b;
    cin>>a>>b;
    get_primes(a);
    for(int i=0;i<cnt;i++)
    {
        int p=primes[i];
        sum[i]=get_nums(a,p)-get_nums(b,p)-get_nums(a-b,p);
    }
    
    vector<int>res;
    res.push_back(1);
    
    for(int i=0;i<cnt;i++)
    {
        for(int j=0;j<sum[i];j++)
        {
            res=mul(res,primes[i]);
        }
    }
    for(int i=res.size()-1;i>=0;i--)printf("%d",res[i]);
    puts("");
    return 0;
}