( A, B )---1*30*2---( 1, 0 )( 0, 1 )
继续一维的实验,这次区别是A和B都由5个点构成。
| A | B | 迭代次数(7e-4) | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0-1*1*1*0*1 | 22047.98995 |
如A为00000,B为11101,在收敛误差为7e-4的时候迭代次数平均为22047次。
得到数据
| A | B | 差值结构 | 迭代次数(7e-4) | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1b | 1b | 1b | 0 | 1b | 0*0*0*0*0-1*1*1*0*1 | 22047.98995 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1b | 0 | 1b | 1b | 1b | 0*0*0*0*0-1*0*1*1*1 | 22053.78894 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1*1*1*1*0-0*0*0*0*0 | 22066.22613 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1*1*1*0*1-0*0*0*0*0 | 22070.00503 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1*0*1*1*1-0*0*0*0*0 | 22073.74372 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0*1*1*1*1-0*0*0*0*0 | 22079.83417 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1b | 1b | 0 | 1b | 1b | 0*0*0*0*0-1*1*0*1*1 | 22089.70854 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1*1*0*1*1-0*0*0*0*0 | 22116.44724 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0-1*1*1*1*0 | 22129.43719 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1b | 1b | 1b | 1b | 0*0*0*0*0-0*1*1*1*1 | 22131.9397 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1*1*1*1*1-0*0*0*0*0 | 27233.71357 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0-1*1*1*1*1 | 27256.31156 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1b | 1b | 0 | 0 | 1b | 0*0*0*0*0-1*1*0*0*1 | 30198.29146 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0*1*1*1*0-0*0*0*0*0 | 30251.94472 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0*0*1*1*1-0*0*0*0*0 | 30282.23618 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1*0*0*1*1-0*0*0*0*0 | 30290.11558 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1*1*0*0*1-0*0*0*0*0 | 30292.66834 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1b | 1b | 1b | 0*0*0*0*0-0*0*1*1*1 | 30317.80905 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1*1*1*0*0-0*0*0*0*0 | 30364.01508 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1b | 1b | 1b | 0 | 0*0*0*0*0-0*1*1*1*0 | 30382.09045 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1b | 0 | 0 | 1b | 1b | 0*0*0*0*0-1*0*0*1*1 | 30425.8392 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0-1*1*1*0*0 | 30430.74372 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | 1*1*1*1*1-0*0*0*0*1 | 31704.21106 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | 1b | k | 0*0*0*0*1-1*1*1*1*1 | 31763.46231 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | k | 1b | 0*0*0*1*0-1*1*1*1*1 | 31823.52261 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | 1b | 1b | 0*1*0*0*0-1*1*1*1*1 | 31842.58794 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | k | 1 | 1 | 1*1*1*1*1-0*0*1*0*0 | 31861.71859 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | k | 1 | 1*1*1*1*1-0*0*0*1*0 | 31878.29146 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | 1b | 1b | 1b | 1b | 1*0*0*0*0-1*1*1*1*1 | 31881.24121 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | k | 1 | 1 | 1 | 1 | 1*1*1*1*1-1*0*0*0*0 | 31909.82915 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | k | 1b | 1b | 0*0*1*0*0-1*1*1*1*1 | 31911.32161 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0-1*0*1*1*0 | 31915.8995 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1*0*1*0*1-0*0*0*0*0 | 31935.78392 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1*1*0*1*0-0*0*0*0*0 | 31972.20603 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0*1*1*0*1-0*0*0*0*0 | 32003 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1b | 1b | 0 | 1b | 0*0*0*0*0-0*1*1*0*1 | 32007.41709 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1b | 0 | 1b | 0 | 1b | 0*0*0*0*0-1*0*1*0*1 | 32043.56784 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0*1*0*1*1-0*0*0*0*0 | 32098.00503 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | k | 1 | 1 | 1 | 1*1*1*1*1-0*1*0*0*0 | 32103.68844 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0-1*1*0*1*0 | 32135.36683 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1b | 0 | 1b | 1b | 0*0*0*0*0-0*1*0*1*1 | 32161.96985 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1*0*1*1*0-0*0*0*0*0 | 32175.60302 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0*0*1*1*0-0*0*0*0*0 | 48545.25126 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0*1*1*0*0-0*0*0*0*0 | 48556.01508 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1*1*0*0*0-0*0*0*0*0 | 48605.37186 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1b | 1b | 0 | 0 | 0*0*0*0*0-0*1*1*0*0 | 48675.65829 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1b | 0 | 0 | 0 | 1b | 0*0*0*0*0-1*0*0*0*1 | 48730.75377 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1b | 1b | 0*0*0*0*0-0*0*0*1*1 | 48771.46734 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1b | 1b | 0 | 0*0*0*0*0-0*0*1*1*0 | 48830.1206 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0-1*1*0*0*0 | 48842.75377 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0*0*0*1*1-0*0*0*0*0 | 48855.59296 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1*0*0*0*1-0*0*0*0*0 | 48950.20603 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1b | 0 | 1b | 0 | 0*0*0*0*0-0*1*0*1*0 | 50898.52261 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1*0*1*0*0-0*0*0*0*0 | 50915.17085 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | k | 1 | 1 | 1 | k | 1*1*1*1*1-1*0*0*0*1 | 50923.64824 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1b | 0 | 0 | 1b | 0*0*0*0*0-0*1*0*0*1 | 50948.99497 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0-1*0*1*0*0 | 51014.21106 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0*1*0*1*0-0*0*0*0*0 | 51085.11055 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0*1*0*0*1-0*0*0*0*0 | 51089.85427 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1*0*0*1*0-0*0*0*0*0 | 51181.0201 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1b | 0 | 0 | 1b | 0 | 0*0*0*0*0-1*0*0*1*0 | 51190.36181 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1b | 0 | 1b | 0*0*0*0*0-0*0*1*0*1 | 51207.30653 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0*0*1*0*1-0*0*0*0*0 | 51320.62814 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | 1*1*1*1*1-0*0*0*1*1 | 51575.8191 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | 1b | 1b | 1b | 1*1*0*0*0-1*1*1*1*1 | 51761.83417 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | k | k | 0*0*0*1*1-1*1*1*1*1 | 51785.37186 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | k | k | 1b | 0*0*1*1*0-1*1*1*1*1 | 51851.21106 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | k | k | 1 | 1*1*1*1*1-0*0*1*1*0 | 52099.34673 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | k | k | 1 | 1 | 1*1*1*1*1-0*1*1*0*0 | 52141.96985 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | k | k | 1 | 1 | 1 | 1*1*1*1*1-1*1*0*0*0 | 52270.17085 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | k | 1b | 1b | 1b | k | 1*0*0*0*1-1*1*1*1*1 | 52584.25628 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | k | k | 1b | 1b | 0*1*1*0*0-1*1*1*1*1 | 52984.98995 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | k | 1 | 1 | k | 1 | 1*1*1*1*1-1*0*0*1*0 | 54980.68342 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | k | 1 | k | 1 | 1 | 1*1*1*1*1-1*0*1*0*0 | 55020.61307 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | 1b | k | 1b | 1b | 1*0*1*0*0-1*1*1*1*1 | 55037.95477 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | k | 1 | k | 1 | 1*1*1*1*1-0*1*0*1*0 | 55176.53266 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | k | 1 | k | 1*1*1*1*1-0*0*1*0*1 | 55465.31658 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | k | 1b | 0*1*0*1*0-1*1*1*1*1 | 55567.94472 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | 1b | k | 0*1*0*0*1-1*1*1*1*1 | 55581.1809 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | k | 1b | 1b | k | 1b | 1*0*0*1*0-1*1*1*1*1 | 55877.77387 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | k | 1 | 1 | k | 1*1*1*1*1-0*1*0*0*1 | 55954.64322 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | k | 1b | k | 0*0*1*0*1-1*1*1*1*1 | 56370.69849 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | k | k | k | 1 | 1*1*1*1*1-0*1*1*1*0 | 91394.07035 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | k | k | k | 1 | 1 | 1*1*1*1*1-1*1*1*0*0 | 92079.35678 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | k | k | 1b | 1b | k | 1*1*0*0*1-1*1*1*1*1 | 92088.8191 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | k | k | k | 0*0*1*1*1-1*1*1*1*1 | 92353.66332 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | k | k | 1 | 1 | k | 1*1*1*1*1-1*1*0*0*1 | 92362.63317 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | k | 1 | 1 | k | k | 1*1*1*1*1-1*0*0*1*1 | 92366.71357 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | k | 1b | 1b | 1*1*1*0*0-1*1*1*1*1 | 92634.03518 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | k | 1b | 1b | k | k | 1*0*0*1*1-1*1*1*1*1 | 92700.88945 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | k | 1*1*1*1*1-0*0*1*1*1 | 92860.34171 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | k | k | k | 1b | 0*1*1*1*0-1*1*1*1*1 | 93350.00503 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | k | k | 1 | k | 1 | 1*1*1*1*1-1*1*0*1*0 | 96071.02513 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | k | 1 | k | k | 1*1*1*1*1-0*1*0*1*1 | 96769.33668 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | k | 1b | k | 1b | k | 1*0*1*0*1-1*1*1*1*1 | 96838.62814 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | k | 1b | k | k | 1b | 1*0*1*1*0-1*1*1*1*1 | 96896.08543 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | k | k | 0*1*0*1*1-1*1*1*1*1 | 97412.50754 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | k | 1b | k | 0*1*1*0*1-1*1*1*1*1 | 97560.26633 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | k | k | 1 | k | 1*1*1*1*1-0*1*1*0*1 | 97703.22613 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | k | 1 | k | k | 1 | 1*1*1*1*1-1*0*1*1*0 | 97748.29146 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | k | 1 | k | 1 | k | 1*1*1*1*1-1*0*1*0*1 | 98111.03518 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | 1b | k | 1b | 1*1*0*1*0-1*1*1*1*1 | 98710.37688 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0*0*0*0*0-0*0*0*0*1 | 106713.7186 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0*0*1*0*0-0*0*0*0*0 | 106716.6583 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0 | 0 | 0*0*0*0*0-0*0*1*0*0 | 106816.5528 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0-1*0*0*0*0 | 107109.1357 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0 | 0 | 0 | 0*0*0*0*0-0*1*0*0*0 | 107147.8693 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0*1*0*0*0-0*0*0*0*0 | 107189.5327 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1*0*0*0*0-0*0*0*0*0 | 107192.4573 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0*0*0*1*0-0*0*0*0*0 | 107282.2764 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0*0*0*0*1-0*0*0*0*0 | 107607.5427 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0 | 0*0*0*0*0-0*0*0*1*0 | 107638.1508 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | k | k | k | 1 | k | 1*1*1*1*1-1*1*1*0*1 | 203142.7236 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | k | k | 1*1*1*1*1-0*1*1*1*1 | 203589.4372 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | k | 1 | k | k | k | 1*1*1*1*1-1*0*1*1*1 | 204060.4322 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | k | k | k | k | 1 | 1*1*1*1*1-1*1*1*1*0 | 205050.3518 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | k | k | 1b | k | k | 1*1*0*1*1-1*1*1*1*1 | 205537.4121 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | k | k | 1 | k | k | 1*1*1*1*1-1*1*0*1*1 | 206108.6633 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | k | k | k | 1b | k | 1*1*1*0*1-1*1*1*1*1 | 206188.3065 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | k | k | k | 0*1*1*1*1-1*1*1*1*1 | 206249.4422 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | k | k | k | k | 1b | 1*1*1*1*0-1*1*1*1*1 | 207548.2965 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | k | 1b | k | k | k | 1*0*1*1*1-1*1*1*1*1 | 209140.0854 |
如果A或B中不包含00000,或者11111则网络似乎都无法收敛,最终收集到可收敛的数据只有122组。
这些数据大体上可以被分为13组
| A | B | 差值结构 | 迭代次数(7e-4) | 等位点数值差 | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0-1*1*1*1*0 | 22129.43719 | 4 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0-1*1*1*1*1 | 27256.31156 | 5 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0-1*1*1*0*0 | 30430.74372 | 3 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | 1b | k | 0*0*0*0*1-1*1*1*1*1 | 31763.46231 | 4 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0-1*0*1*1*0 | 31915.8995 | 3 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0-1*1*0*0*0 | 48842.75377 | 2 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0-1*0*1*0*0 | 51014.21106 | 2 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | k | k | 0*0*0*1*1-1*1*1*1*1 | 51785.37186 | 3 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | 1b | k | 0*1*0*0*1-1*1*1*1*1 | 55581.1809 | 3 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | k | k | k | 0*0*1*1*1-1*1*1*1*1 | 92353.66332 | 2 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | k | k | 0*1*0*1*1-1*1*1*1*1 | 97412.50754 | 2 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0-1*0*0*0*0 | 107109.1357 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | k | k | k | 0*1*1*1*1-1*1*1*1*1 | 206249.4422 | 1 |

这些数据的迭代次数与等位点数值差之间总体上呈反比关系,但有误差
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0-1*1*1*0*0 | 30430.74372 | 3 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0-1*0*1*1*0 | 31915.8995 | 3 |
如这两组的等位点数值差都是3但是,一个的差值结构是1b,1b,1b,0,0.而另一个是1b,0,1b,1b,0.间距的差异无法从差值上体现出来。
为表达这种差异引入一个变量j让1b,0,1b,1b,0的等位点数值差为3+j
重新整理所有的等位点数值差得到
| A | B | 差值结构 | 迭代次数(7e-4) | 等位点数值差 | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0-1*1*1*1*0 | 22129.43719 | 4 | 4 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0-1*1*1*1*1 | 27256.31156 | 5 | 5 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0-1*1*1*0*0 | 30430.74372 | 3 | 3 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | 1b | k | 0*0*0*0*1-1*1*1*1*1 | 31763.46231 | 4 | 4+k |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0-1*0*1*1*0 | 31915.8995 | 3 | 3+j |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0-1*1*0*0*0 | 48842.75377 | 2 | 2 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0-1*0*1*0*0 | 51014.21106 | 2 | 2+j |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | 1b | k | k | 0*0*0*1*1-1*1*1*1*1 | 51785.37186 | 3 | 3+2k |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | 1b | k | 0*1*0*0*1-1*1*1*1*1 | 55581.1809 | 3 | 3+2k+j |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | 1b | k | k | k | 0*0*1*1*1-1*1*1*1*1 | 92353.66332 | 2 | 2+3k |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | 1b | k | k | 0*1*0*1*1-1*1*1*1*1 | 97412.50754 | 2 | 2+3k+j |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0-1*0*0*0*0 | 107109.1357 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1b | k | k | k | k | 0*1*1*1*1-1*1*1*1*1 | 206249.4422 | 1 | 1+4k |
设置k和j的值让这组数据的大小关系得以成立
| 差值结构 | 迭代次数(7e-4) | 等位点数值差 | |||||||
| 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0-1*1*1*1*0 | 22129.43719 | 4 | 4 | 4 |
| 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0-1*1*1*1*1 | 27256.31156 | 5 | 5 | 5 |
| 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0-1*1*1*0*0 | 30430.74372 | 3 | 3 | 3 |
| 1b | 1b | 1b | 1b | k | 0*0*0*0*1-1*1*1*1*1 | 31763.46231 | 4 | 4+k | 2.7 |
| 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0-1*0*1*1*0 | 31915.8995 | 3 | 3+j | 2.1 |
| 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0-1*1*0*0*0 | 48842.75377 | 2 | 2 | 2 |
| 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0-1*0*1*0*0 | 51014.21106 | 2 | 2+j | 1.1 |
| 1b | 1b | 1b | k | k | 0*0*0*1*1-1*1*1*1*1 | 51785.37186 | 3 | 3+2k | 0.4 |
| 1b | k | 1b | 1b | k | 0*1*0*0*1-1*1*1*1*1 | 55581.1809 | 3 | 3+2k+j | -0.5 |
| 1b | 1b | k | k | k | 0*0*1*1*1-1*1*1*1*1 | 92353.66332 | 2 | 2+3k | -1.9 |
| 1b | k | 1b | k | k | 0*1*0*1*1-1*1*1*1*1 | 97412.50754 | 2 | 2+3k+j | -2.8 |
| 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0-1*0*0*0*0 | 107109.1357 | 1 | 1 | 1 |
| 1b | k | k | k | k | 0*1*1*1*1-1*1*1*1*1 | 206249.4422 | 1 | 1+4k | -4.2 |
比如让k=-1.3,j=-0.9
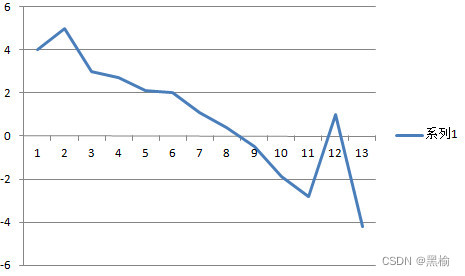
这样做的代价是两组边界值1b,0,0,0,0;1b,1b,1b,1b,1b出现错误,但其他的值都可以被正确排序。


![[BSidesCF 2019]SVGMagic (XXE)](https://img-blog.csdnimg.cn/793cee4441c341c8a301eb0e5680872f.png)