分享今天看到的一个题目,不同思路解法
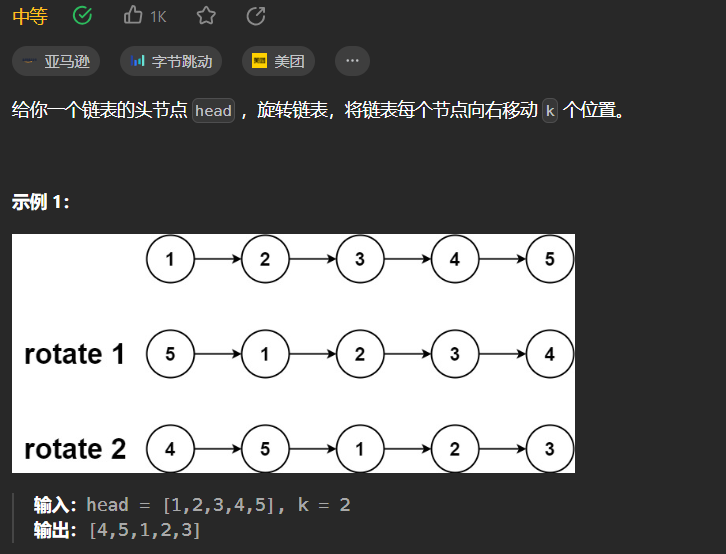
题目


思路1:时间复杂度0(N*k)
void rotate(int *a,int N,int k)//N为数组元素个数
{
while(k--)
{
int tem=a[N-1];
for(int right=N-2;right>=0;right--)
{
a[right+1]=a[right];
}
a[0]=tem;
}
}
思路2(开辟一块空间):时间复杂度0(N) 空间复杂度o(N)
void rotate(int *a,int N,int k,int *b)//数组b int b[sz]={0};
{
for(int i=0;i<k;i++)
{
b[i]=a[N-i-1];
}
for(int =k;i<N;i++)
{
b[i]=a[N-i-1];
}
}
思路三单独逆置后整体逆置:
void Rt(int *a,int left,int right)//对区间[left:right]内的元素进行内置
{
while(left<=right)
{
int tem=a[left];
a[left]=a[right];
a[right]=tem;
++left;
--right;
}
}
void rotate(int *a,int N;int k)
{
Rt(a,N-k,N-1);//先逆序数组a的后k个 1 2 3 4 7 6 5
Rt(a,0,N-k-1);//再逆序数组a前N-k个 4 3 2 1 7 6 5
Rt(a,0,N);//最后逆序整个数组a 5 6 7 1 2 3 4
}
左后对上面代码进行分析,上述是以N=7,k=3的情况(k<N)。那么如果k>N怎么办N-k不是变成负数了吗?上述代码就显然不成立了。
但是我们可以发现当k=N时数组没有变化,所以可以看成逆序每N次一个循环,所以只要在主函数对函数rotate函数进行传参是传入k%Nj就能使上述代码依然成立了。