1.遍历二叉树
在二叉树的一些应用中,常常要求在树中查找具有某种特征的结点,或者对树中全部结点逐一进行某种处理。这就引入了遍历二叉树的问题,即如何按某条搜索路径访问树中的每一个结点,使得每一个结点仅且仅被访问一次。
遍历二叉树:是指按照某种方法顺着某一条搜索路径寻访二叉树的结点,使得每个结点均被访问一次且仅被访问一次。
1.递归遍历
一棵二叉树由根结点、根结点的左子树和根结点的右子树3部分组成,因而只要依次遍历这3部分,就能遍历整棵二叉树。
遍历的次序:假如以L、D、R分别表示遍历左子树、遍历根结点和遍历右子树,遍历整个二叉树则有DLR、LDR、LRD、DRL、RDL、RLD六种遍历方案。若规定先左后右,则只有前三种情况,分别规定为:
DLR——先(根)序遍历,
LDR——中(根)序遍历,
LRD——后(根)序遍历。
1.先序遍历
先序遍历二叉树算法的框架是 :若二叉树为空,遍历结束,否则: 访问根结点; 先序遍历根结点的左子树; 先序遍历根结点的右子树。

void PreOrder(BiTree bt) /* bt为指向根结点的指针*/
{
if (bt) /*如果bt为空,结束*/
{
visit (bt ); /*访问根结点*/
PreOrder (bt -> lchild); /*先序遍历左子树*/
PreOrder (bt -> rchild); /*先序遍历右子树*/
}
}
2.中序遍历
中序遍历二叉树算法的框架是: 若二叉树为空,遍历结束,否则: 中序遍历根结点的左子树; 访问根结点; 中序遍历根结点的右子树。

void InOrder(BiTree bt)/* bt为指向二叉树根结点的指针*/
{
if (bt ) /*如果bt为空,结束*/
{
InOrder (bt -> lchild); /*中序遍历左子树*/
Visit (bt); /*访问根结点*/
InOrder (bt -> rchild); /*中序遍历右子树*/
}
}
3.后序遍历
后序遍历二叉树算法的框架是:若二叉树为空,遍历结束,否则 后序遍历根结点的左子树; 后序遍历根结点的右子树; 访问根结点。

void PostOrder(BiTree bt)
/* bt为指向二叉树根结点的指针*/
{
if (bt ) /*如果bt为空,结束*/
{
PostOrder (bt -> lchild);/*后序遍历左子树*/
PostOrder (bt -> rchild);/*后序遍历右子树*/
visit (bt ); /*访问根结点*/
}
}
通过上述三种不同的遍历方式得到三种不同的线性序列,它们的共同的特点是有且仅有一个开始结点和一个终端结点,其余各结点都有且仅有一个前驱结点和一个后继结点。
从二叉树的遍历定义可知,三种遍历算法的不同之处仅在于访问根结点和遍历左右子树的先后关系。如果在算法中隐去和递归无关的语句visit(),则三种遍历算法是完全相同的。遍历二叉树的算法中的基本操作是访问结点,显然,不论按那种方式进行遍历,对含n个结点的二叉树,其时间复杂度均为O(n)。所含辅助空间为遍历过程中占的最大容量,即树的深度。最坏的情况下为n,则空间复杂度也为O(n)。
4.层序遍历
二叉树的层次遍历:是指从二叉树的第一层(根结点)开始,从上至下逐层遍历,在同一层中,按从左到右的顺序对结点逐个进行访问。

利用队列来实现 :
算法思想:遍历从二叉树的根结点开始,首先将根结点入队列,然后执行下面的操作:
1)取出队头元素;
2) 访问该元素所指结点;
3) 若该元素所指结点的左、右孩子结点非空,则将该元素所指结点的左孩子指针和右孩子指针入队。
4)若队列非空,重复1)-3);当队列为空时,二叉树的层次遍历结束。
void LevelOrder( BiTree bt) /*层次遍历二叉树bt算法*/
{ 初始化队列Q;
if ( bt == NULL ) return;
bt入队列Q;
while( 队列Q不空){
p出队元素;
Visit( p); /*访问出队结点*/
if ( p->lchild) /*队首结点左孩子不空,入队*/
{ p->lchild入队Q }
if (p->rchild) /*队首结点右孩子不空,入队*/
{ p->rchild入队Q }
}
}
5.练习
1.找出分别满足下面条件的所有二叉树(非空形态):
(a)前序序列和中序序列相同;
(b)中序序列和后序序列相同;
(c)前序序列和后序序列相同;
(d)前序序列、中序序列和后序序列都相同。
2.已知一棵二叉树的中序序列和后序序列分别为BDCEAFHG和DECBHGFA,画出这棵二叉树。

结论:
1) 由二叉树的前序序列和中序序列可以唯一确定这棵二叉树。
2) 由二叉树的后序序列和中序序列可以唯一确定这棵二叉树。
3) 由二叉树的前序序列和后序序列不能唯一确定这棵二叉树。
2.非递归遍历
二叉树前序遍历的非递归算法的关键:在前序遍历过某结点的整个左子树后,如何找到该结点的右子树的根指针。
解决办法:在访问完该结点后,将该结点的指针保存在栈中,以便以后能通过它找到该结点的右子树。

1.先序遍历
先序算法执行轨迹
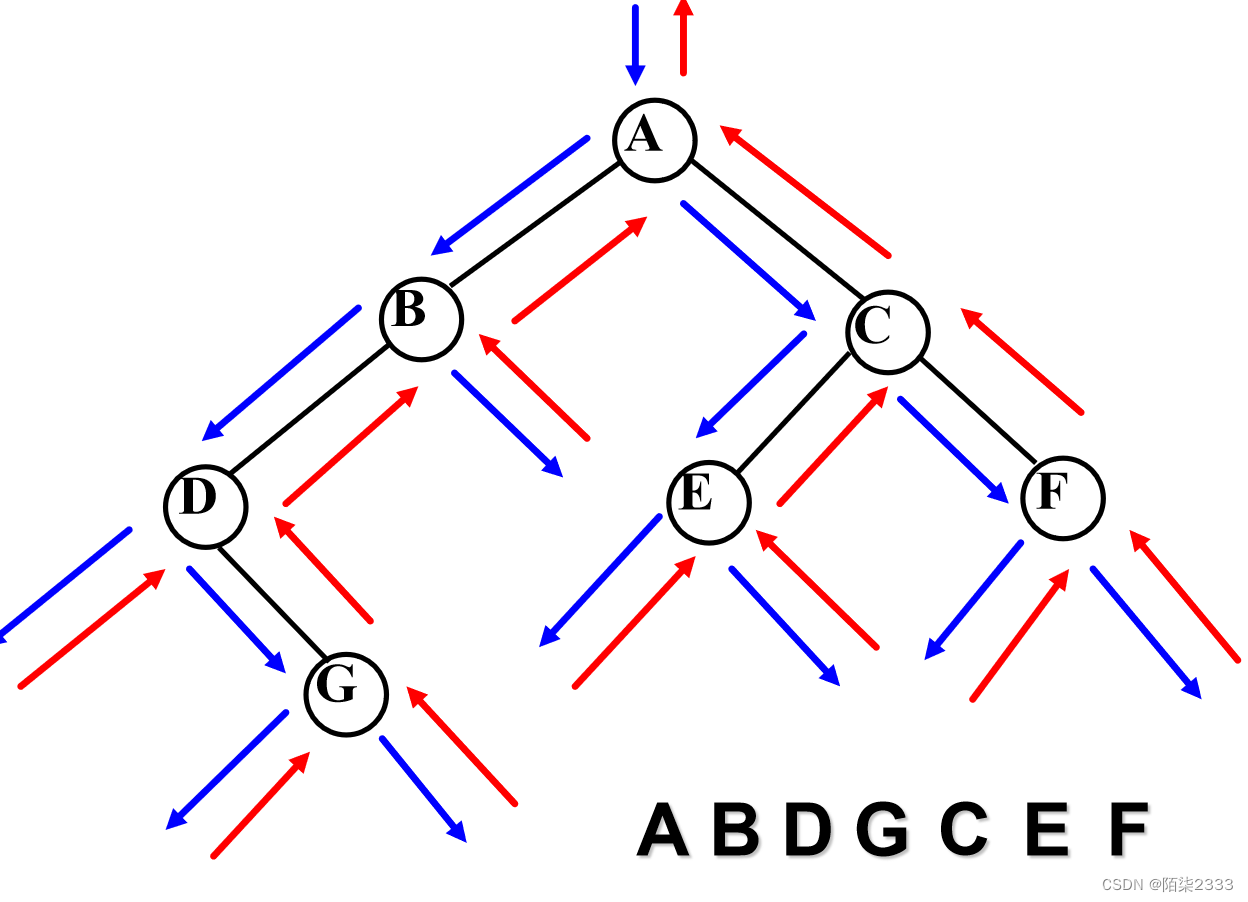
步骤:
1.栈s初始化;
2.循环直到root为空或栈s为空
2.1 当root不空时循环
2.1.1 输出root->data;(可将输出变为任何处理)
2.1.2 将指针root的值保存到栈中;
2.1.3 继续遍历root的左子树
2.2 如果栈s不空,则
2.2.1 将栈顶元素弹出至root;
2.2.2 准备遍历root的右子树;
//先序遍历
Void Firstorder(BiTree bt)
{ p=bt; /*根结点为当前结点*/
S=Initial( ); /*初始化栈*/
While(p||!Empty(S))
{
While(p) /*当前结点不空*/
{ visit(p); /*访问结点*/
Push(S,p); /*当前结点入栈*/
p=p->Lchild; /*左孩子作为当前结点*/
}
If(!Empty(S)) /*栈不空*/
{
p=pop(s); /*出栈*/
p=p->Rchild; /*右孩子作为当前结点*/
}
}
}
2.中序遍历
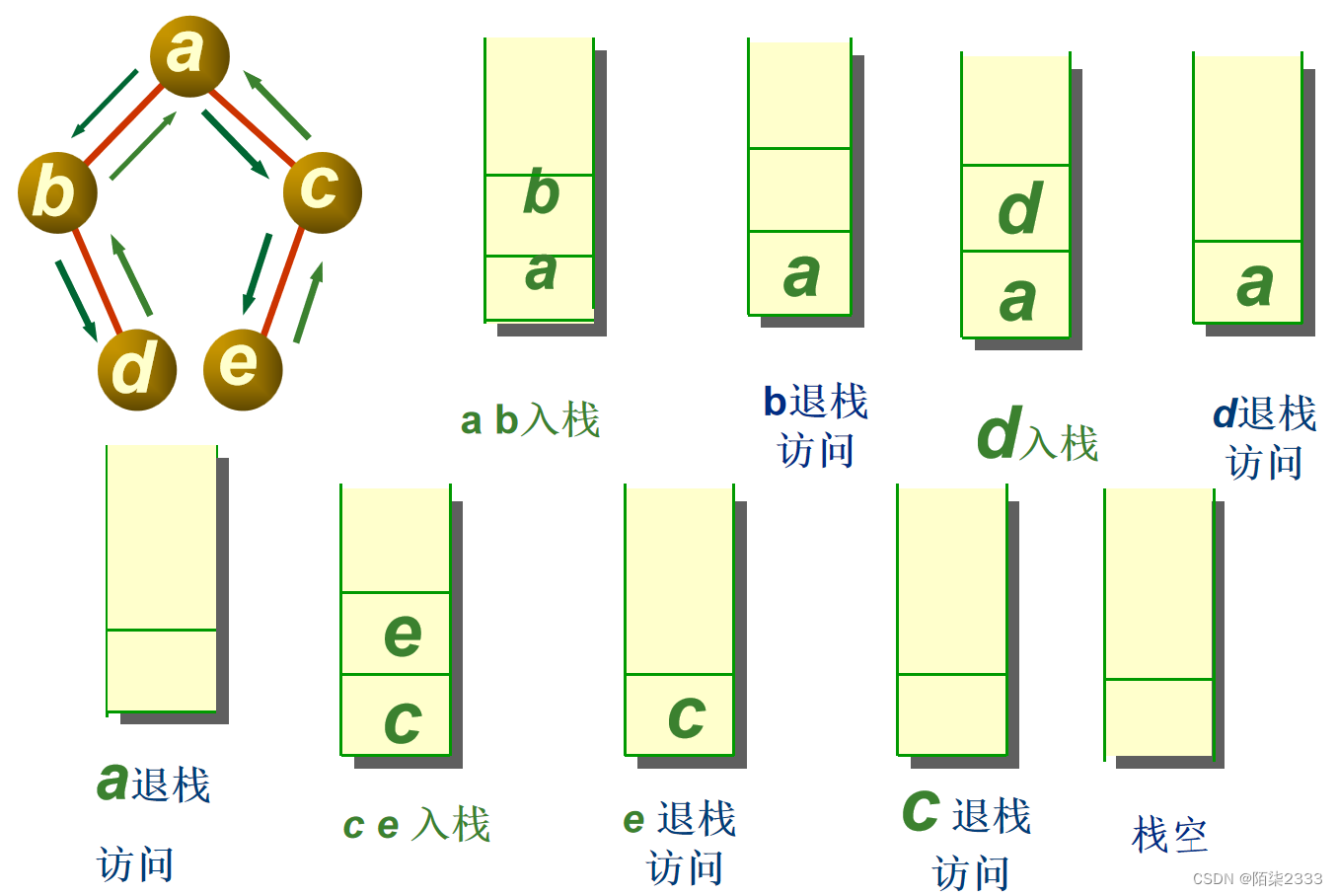
//中序遍历
Void Inorder(BiTree bt)
{ p=bt; /*根结点为当前结点*/
S=Initial( ); /*初始化栈*/
While(p||!Empty(S))
{
While(p) /*当前结点不空*/
{
Push(S,p); /*当前结点入栈*/
p=p->Lchild; /*左孩子作为当前结点*/
}
If(!Empty(S)) /*栈不空*/
{
p=pop(s); /*出栈*/
Visit(p); /*访问结点*/
p=p-Rchild; /*右孩子作为当前结点*/
}
}
}3.后序遍历
typedef enum{L,R} tagtype; /*定义枚举类型*/
typedef struct {
Bitree ptr;
tagtype tag;
}stacknode; /*定义栈结点类型*/
typedef struct{
stacknode Elem[maxsize];
int top;
}SqStack; /*定义顺序栈*/
void PostOrderUnrec(Bitree bt) /*后序遍历算法*/
{ p=bt;
If(!p) return;
do
{ while (p) /*遍历左子树*/
{
x.ptr = p;
x.tag = L; /*标记为左子树*/
push(s,x); /*入栈*/
p=p->lchild; /*左孩子作为当前结点*/
}
while (!StackEmpty(s) && s.Elem[s.top].tag==R) {
x = pop(s);
p = x.ptr;
visite(p); //tag为R,表示右子树访问完毕,故访问根结点
}
if (!StackEmpty(s)){
s.Elem[s.top].tag =R; /*遍历右子树*/
p=s.Elem[s.top].ptr->rchild; /*右孩子作为当前结点*/
}
}while (!StackEmpty(s));
}
4.练习
1.交换二叉树各结点的左、右子树(递归算法)
void unknown ( BiTree T )
{
BiTreeNode *p = T, *temp;
if ( p != NULL )
{
temp = p->lchild;
p->lchild = p->rchild;
p->rchild = temp;
unknown ( p->lchild );
unknown ( p->rchild );
}
}
2.不用栈消去递归算法中的第二个递归语句 (即消去尾递归)
void unknown ( BiTree T )
{
BiTreeNode *p = T, *temp;
while ( p != NULL )
{
temp = p->lchild;
p->lchild = p->rchild;
p->rchild = temp;
unknown ( p->lchild );
p = p->rchild;
}
}3.使用栈消去递归算法中的两个递归语句
void unknown ( BiTree T )
{
BiTreeNode *p, *temp,S[Max];
int top=-1;
if ( T != NULL )
{
top++;S[top]= T;
while ( top>-1 )
{
p=S[top]; top--; /*栈中退出一个结点*/
temp = p->lchild; /*交换子女*/
p->lchild = p->rchild;
p->rchild = temp;
if ( p->rchild != NULL )
top++;S[top]= p->rchild;
if ( p->lchild != NULL )
top++;S[top]= p->p->lchild;
}
}
}
2.应用
1.设计算法输出二叉树的所有叶子结点的值。
基本思想:
若二叉树为空树,则叶子数目为0。
对于一棵非空二叉树,如果它的左子树和右子树都为空,那么此二叉树只有一个结点,就是叶子,此时叶子数目为1;否则,二叉树的叶子数目为左子树叶子数目和右子树叶子数目的总和。
int BitreeLeaf ( BiTree bt )
{
if ( bt == NULL ) return 0 ; /* 空树,叶子数为0 */
if ( bt->lchild ==NULL&& bt->rchild == NULL)
return 1 ; /*只有一个根结点,叶子数为1*/
return ( BitreeLeaf ( bt -> lchild ) + BitreeLeaf ( bt -> rchild )) ;
}
2.设计算法求二叉树的深度。
基本思想:
若二叉树为空,约定二叉树的深度为0;
对于一棵二叉树,如果它的左子树和右子树都为空,那么此二叉树只有一个根结点,此时二叉树的深度为1;否则,先求出其左、右子树的深度depthL和depthR,那么整棵二叉树的深度为1+max(depthL,depthR)。
int BitreeDepth ( BiTree bt )
{ int d = 0,depthL, depthR; /*depthL和depthR分别为左、右子树的深度*/
if ( bt == NULL ) return 0 ; /*空树,深度为0 */
if ( bt -> lchild ==NULL && bt -> rchild == NULL) return 1; /*叶子结点,深度为1 */
depthL = BitreeDepth ( bt -> lchild ) ; /*左子树深度 */
depthR = BitreeDepth ( bt -> rchild ) ; /*右子树深度 */
d = max (depthL , depthR ) /*d为左右子树中较深者的深度*/
return d+1 ; /* 整棵二叉树的深度为左、右子树中较深者的深度+1 */
}
3.创建二叉树
创建二叉树的方法有两种,一种是给定一棵二叉树的先序遍历序列和中序遍历序列创建二叉树,另一种是给定一棵二叉树的“扩展先序遍历序列”创建二叉树。
(1)结合先序遍历序列和中序遍历序列创建二叉树
基本思想:
先序遍历的第一个结点一定是二叉树的根结点,而根据中序遍历规则,这个结点将同一棵二叉树的中序遍历序列分成了左、右两部分,左边部分是二叉树的根结点的左子树的中序遍历序列,右边部分是二叉树的根结点的右子树的中序遍历序列。根据这两个子序列,在先序序列中找到对应的子序列,左子序列的第一个结点为左子树的根结点,右子序列的第一个结点为右子树的根结点。对左右子树,再反复利用这个方法,最终根据先序序列和中序序列能唯一地确定出一棵二叉树。
(2)结合“扩展先序遍历序列”创建二叉树。
扩展先序遍历序列:
就是先对原有二叉树用空子树进行扩展,使每个结点的左右子树(包括空子树)都存在,然后再对扩展后的二叉树进行先序遍历。遍历序列中用特定的符号表示空子树。
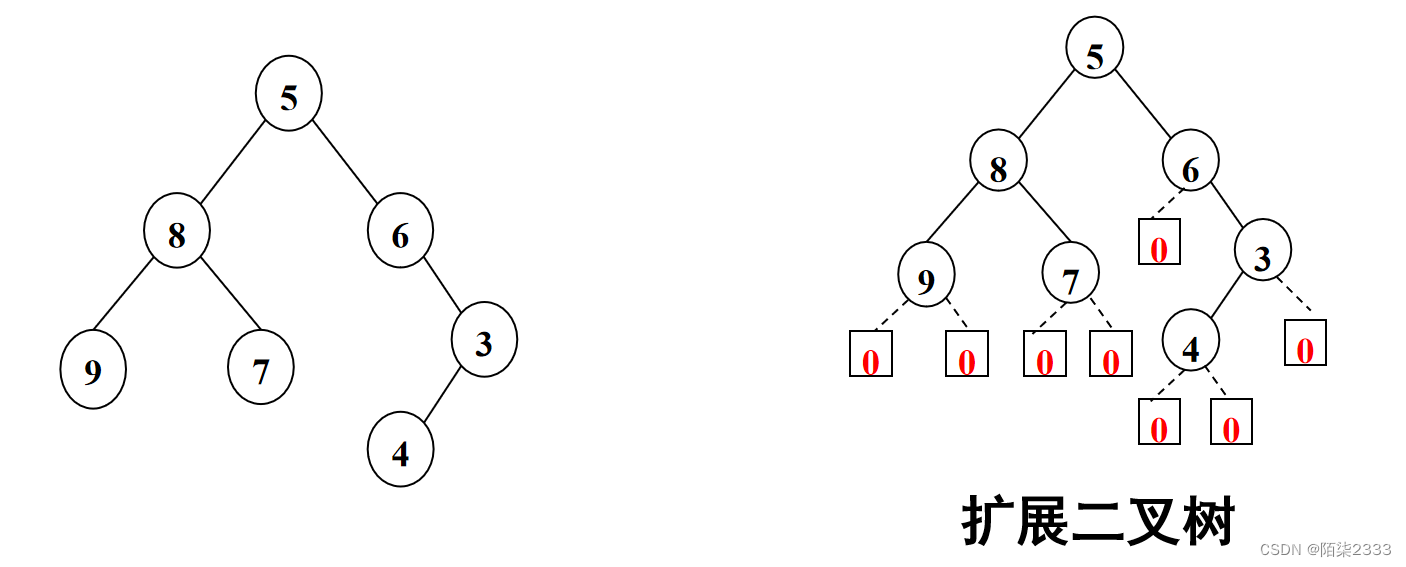
其扩展先序遍历序列为:
5 8 9 0 0 7 0 0 6 0 3 4 0 0 0
其中“0”表示空子树。
BiTree CreateBiTree(char str[])
{ BiTree bt;
static int i=0;
char c = str[i++];
if( c==‘.’ ) bt = NULL;/* 创建空树 */
else
{ bt = (BiTree)malloc(sizeof(BiTreeNode));
bt->data = c; /* 创建根结点 */
bt->lchild = CreateBiTree(str);
/* 创建左子树 */
bt->rchild = CreateBiTree(str);
/* 创建右子树 */
}
return bt;
}










![[Android]使用Git将项目提交到GitHub](https://img-blog.csdnimg.cn/275fc29f07c546c3b3a08c17184e32ac.png)