聚类笔记/sklearn笔记：Affinity Propagation亲和力传播

news2024/9/25 19:18:31

1 算法原理

1.1 基本思想

将全部数据点都当作潜在的聚类中心(称之为 exemplar )
然后数据点两两之间连线构成一个网络( 相似度矩阵 )
再通过网络中各条边的消息( responsibility 和 availability )传递计算出各样本的聚类中心。

1.2 主要概念

Examplar	聚类中心
similarity S(i,j)	相似度一般使用负的欧式距离，所以 S(i,j) 越大，表示两个点距离越近，相似度也就越高
Preference	点 i 作为聚类中心的参考度(不能为0)，取值为 S相似度对角线的值此值越大，则为聚类中心的可能性就越大。如果没有被设置，则一般设置为 S相似度值的中值
Responsibility 吸引度	点 `k` 适合作为数据点 `i` 的聚类中心的程度，记为 `r(i,k)` 。
Availability 归属度	点 `i` 选择点 `k` 作为其聚类中心的适合程度，记为 `a(i,k)` r和a都是第二个参数的点作为聚类中心
Damping factor 阻尼系数	主要是起收敛作用

1.3 算法流程

计算相似度矩阵
- 此时对角线上的值都是0，用某种方法（固定参数/相似度矩阵的中位值/最小值等）填充对角线的值
开始时：构造一个全0的归属度矩阵a
以下不断迭代更新
- 更新每一个吸引度矩阵r中的单元格值
- 更新归属度矩阵a
- 使用阻尼系数更新归属度a和吸引度r
  - 使用阻尼系数(damping factor)来衰减吸引度和归属度信息，以免在更新的过程中出现数值振荡
  - 上面三个公式算出来的是等号右边的a和r
获取聚类中心

1.4 举例

假设有如下样本：共5个维度
计算相似度矩阵
- 相似度矩阵中每个单元是用两个样本对应值的差的平方和取负值得到的，对角线上的除外
- 当聚类中心为对角线上的单元格选择了比较小的值，那么AP算法会快速收敛并得到少量的聚类中心，反之亦然。因此。我们使用表格中最小的值 -22 去填充相似度矩阵中的 0 对角线单元格。
计算吸引度矩阵r
- eg：计算 Bob对 Alice的吸引度（Responsibility）【Alice视Bob为聚类中心的程度，r(Alice,Bob)
  - 这里套用上面的公式即为：用S(Bob,Alice)- max(a(Alice,others)+s(Alice,others))
    - 即 -7-(-6)=-1
计算归属度矩阵a
- - 以alice为例,a(Alice,Alice)就是所有大于0的 r(others,Alice)的和，即10+11=21
- - 以Alice支持Bob作为其聚类中心为例
  - a(Alice,Bob)=min(0,r(Bob,Bob)+0)=-15 【没有r(others,Bob)大于0】
假设迭代一次就结束，那么我们计算评估矩阵
- c=r+a
- 一般将评估矩阵中取得最大值的一些点作为聚类中心
  - Alice，Bob 和 Cary 共同组成一个聚类簇
  - Doug 和 Edna 则组成了第二个聚类

1.5 主要缺点

Affinity Propagation的主要缺点是其复杂性。该算法的时间复杂度为 $O(N^2 \times I)$ ，其中 N 是样本数量，I 是直到收敛的迭代次数
如果使用密集的相似性矩阵，则内存复杂度为 $O(n^2)$ ，但如果使用稀疏的相似性矩阵则可以降低。
这使得Affinity Propagation最适合小到中等大小的数据集

2 sklearn实现

class sklearn.cluster.AffinityPropagation(
    *, 
    damping=0.5, 
    max_iter=200, 
    convergence_iter=15, 
    copy=True, 
    preference=None, 
    affinity='euclidean', 
    verbose=False, 
    random_state=None)

2.1 主要参数

damping	float，默认为0.5 阻尼因子，取值范围是[0.5, 1.0)
max_iter	int，默认为200 最大迭代次数
convergence_iter	int，默认为15 估计的簇数量没有变化的迭代次数，达到该次数则停止收敛
preference	array-like形状为(n_samples,)或浮点数，默认为None 每个点的偏好 - 具有较大偏好值的点更有可能被选择为典型样本如果没有传递偏好作为参数，它们将被设置为输入相似度的中值。
affinity	{‘euclidean’, ‘precomputed’}，默认为‘euclidean’ 使用哪种亲和力。目前支持‘precomputed’和欧几里得。‘euclidean’使用点之间的负平方欧几里得距离。

2.2 主要属性

from sklearn.cluster import AffinityPropagation
import numpy as np

X = np.array([[1, 2], [1, 4], [1, 0],
              [10, 2], [10, 4], [10, 0]])

ap=AffinityPropagation(damping=0.8).fit(X)

cluster_centers_indices_	簇中心的索引
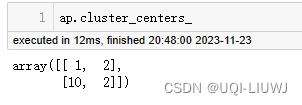
cluster_centers_	簇中心
labels_	每个点的标签
affinity_matrix_	亲和力矩阵
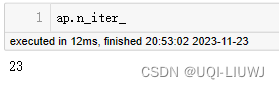
n_iter_	收敛所需的迭代次数