一.引例（哥尼斯堡七桥问题）

        哥尼斯堡七桥问题是指在哥尼斯堡市（今属俄罗斯）的普雷格尔河（Pregel River）中，是否可以走遍每座桥一次且仅一次，最后回到起点的问题。这个问题被认为是图论的开端，也是数学史上著名的问题之一。

        欧拉在解决这个问题时，将问题转化为了图论中的欧拉回路问题。他证明了如果一个图中有欧拉回路，那么这个图中每个顶点的度数都是偶数。反之，如果每个顶点的度数都是偶数，那么这个图中就存在欧拉回路。

        因此，哥尼斯堡七桥问题的答案是否定的，因为哥尼斯堡的地图中有两个岛屿，这两个岛屿与其他地区相连的桥的数量都是奇数，因此这个图中不存在欧拉回路。

二.图的逻辑结构

1.图的定义

图是由顶点的有穷非空集合和顶点之间边的几何组成。

通常表示为：G=（V，E）

注：

1）G表示一个图

2）V是图G中顶点的集合

3）E是图G中顶点之间边的集合

4）在线性表中，元素的个数可以为0，称之为空表；在树中，元素的个数可以为0，称之为空树；但是在图中，顶点个数不能为0，可以没有边。

2.有向图与无向图

若顶点vi和vj之间的边没有方向，则称这条边为无向边，表示为（vi，vj）

如果图的任意两个顶点之间的边都是无向边，则称该图为无向图。

若顶点vi和vj之间的边有方向，则称这条边为有向边，表示为<vi，vj>

如果图的任意两个顶点之间的边都是有向边，则称该图为有向图。

3.图的基本术语

1）简单图

在图中，若不存在顶点到自身的边，且同一条边不重复出现。

注：数据结构中讨论的都是简单图

2）邻接/依附

无向图中，对于任意两个顶点vi和vj，若存在边（vi，vj），则称顶点vi和顶点vj互为邻接点，同时称边（vi，vj）依附于顶点vi和顶点vj。

有向图中，对于任意两个顶点vi和vj，若存在弧<vi,vj>，则称顶点vi邻接到顶点vj，顶点vj邻接自顶点vi，同时称弧<vi，vj>依附于顶点vi和顶点vj。

3）无向完全图/有向完全图

无向完全图：

在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。

含有n个顶点的无向完全图中边的个数：

n*（n-1）/2

有向完全图：

在有向图中，如果任意两个顶点之间都存在方向相反的两条弧，则称该图为有向完全图。

含有n个顶点的有向完全图中边的个数：

n*（n-1）

4）稀疏图/稠密图

稀疏图：边数很少的图

稠密图：边数很多的图

5）度

无向图：TD（v）

入度：ID（v）

出度：OD（v）

6）度与边数的关系

所有顶点的度之和=边数*2

入度=出度=边数

7）权/网

权：对边赋予的有意义的数值量

（从一个顶点到另一个顶点所需要付出的代价）

网：边上带权的图

8）路径长度

非带权图：边的个数

带权图：各边权之和

9）简单回路

除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路。

10）连通图

图中任意两个顶点都是联通的

11）连通分量

非连通图的极大连通子图

12）强连通图

在有向图中，堆图中任意一对顶点vi和vj（i！=j），若从顶点vi到顶点vj和从顶点vj到顶点vi均有路径

13）生成树

n个顶点的连通图G的生成树是包含G中全部顶点的一个极小连通子图

含有n-1条边

生成树不是唯一的

14）生成森林

在非连通图中，由每个连通分量都可以得到一棵生成树，这些连通分量的生成树就组成了一个非连通图的生成森林。

4.不同结构中逻辑关系的对比

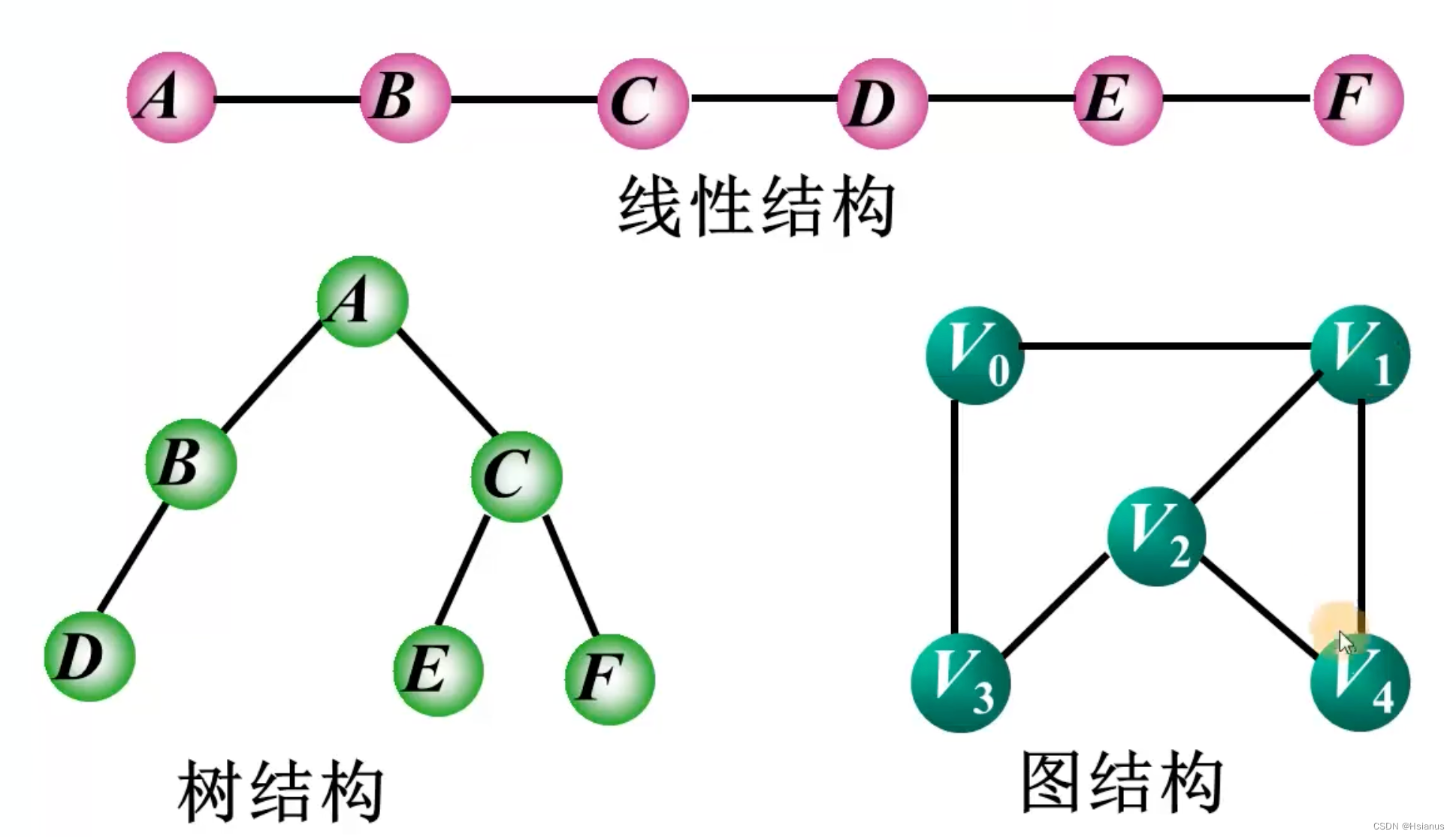
在线性结构中，数据元素之间仅具有线性关系。

在树结构中，结点之间具有层次关系。

在图结构中，任意两个顶点之间都可能有关系。

在线性结构中，元素之间的关系为前驱和后继。

在树结构中，结点之间的关系为双亲和孩子。

在图结构中，顶点之间的关系为邻接。

三.图的抽象数据类型定义

ADT Graph

Data

        顶点的有穷非空集合和边的集合

Operation

初始

销毁

深度优先搜索

广度优先搜索