https://github.com/Nightmare4214/re_nfa_dfa
前置知识
ϵ \epsilon ϵ代表空串
语言
某个给定字母表上一个任意的可数的串集合
正则语言/正则表达式
正则语言(regular language)/正则表达式(regular expression)
每个正则表达式
r
r
r表示一个语言
L
(
r
)
L\left(r\right)
L(r)
归纳基础:
1)
ϵ
\mathbf{\epsilon}
ϵ是一个正则表达式,
L
(
ϵ
)
=
{
ϵ
}
L\left(\mathbf{\epsilon}\right)=\left\{\epsilon\right\}
L(ϵ)={ϵ},即该语言只包含空串
2)如果
a
a
a是
Σ
\Sigma
Σ上的一个符号,那么
a
\mathbf{a}
a是一个正则表达式,并且
L
(
a
)
=
{
a
}
L\left(\mathbf{a}\right)=\left\{a\right\}
L(a)={a}
归纳步骤:
假定
r
,
s
\mathbf{r},\mathbf{s}
r,s都是正则表达式,分别表示语言
L
(
r
)
,
L
(
s
)
L\left(\mathbf{r}\right),L\left(\mathbf{s}\right)
L(r),L(s),那么:
1)
(
r
)
∣
(
s
)
\left(\mathbf{r}\right)|\left(\mathbf{s}\right)
(r)∣(s)是一个正则表达式,表示语言
L
(
r
)
∪
L
(
s
)
L\left(\mathbf{r}\right)\cup L\left(\mathbf{s}\right)
L(r)∪L(s)
2)
(
r
)
(
s
)
\left(\mathbf{r}\right)\left(\mathbf{s}\right)
(r)(s)是一个正则表达式,表示语言
L
(
r
)
L
(
s
)
L\left(\mathbf{r}\right)L\left(\mathbf{s}\right)
L(r)L(s)
3)
(
r
)
∗
\left(\mathbf{r}\right)^*
(r)∗是一个正则表达式,表示语言
(
L
(
r
)
)
∗
\left(L\left(\mathbf{r}\right)\right)^*
(L(r))∗
4)
(
r
)
\left(\mathbf{r}\right)
(r)是一个正则表达式,表示语言
L
(
r
)
L\left(\mathbf{r}\right)
L(r)
有穷自动机
有穷自动机是识别器,他们只能对每个可能的输入串简单地回答“是”或“否”
有穷自动机分为不确定的有穷自动机和确定的有穷自动机
不确定的有穷自动机
不确定的有穷自动机(Nondeterministic Finite Automata, NFA)对其边上的标号没有任何限制。一个符号标记离开同意状态的多条边,并且空串
ϵ
\epsilon
ϵ也可以作为标号
N
F
A
A
=
(
Q
,
Σ
,
δ
,
q
0
,
F
)
NFA\ A=\left(Q,\Sigma,\delta,q_0,F\right)
NFA A=(Q,Σ,δ,q0,F)
1)一个有穷的状态集合
Q
Q
Q
2)一个输入的符号集合
Σ
\Sigma
Σ,即输入字母表。我们假定空串
ϵ
\epsilon
ϵ不是
Σ
\Sigma
Σ中的元素
3)一个转换函数,它为每个状态和
Σ
∪
{
ϵ
}
\Sigma\cup \left\{\epsilon\right\}
Σ∪{ϵ}中的每个符号都给出了相应的后继状态的集合,
即
δ
:
Q
×
(
Σ
∪
{
ϵ
}
)
↦
P
(
Q
)
\delta: Q \times \left(\Sigma\cup \left\{\epsilon\right\}\right) \mapsto \mathcal{P}\left(Q\right)
δ:Q×(Σ∪{ϵ})↦P(Q),其中
P
(
Q
)
\mathcal{P}\left(Q\right)
P(Q)代表
Q
Q
Q的所有子集组成的集合
4)
Q
Q
Q中的一个状态
s
0
s_0
s0被指定为开始状态,或者说初始状态
5)
Q
Q
Q的一个子集
F
F
F被指定为接收状态(或者说终止状态)的集合
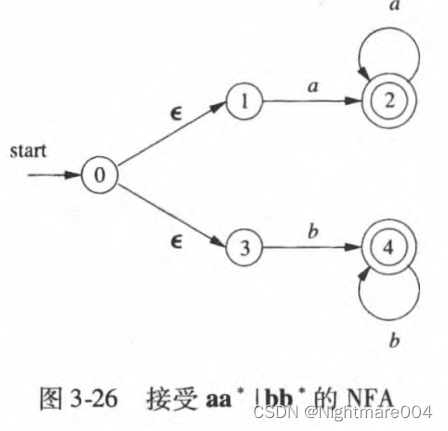
确定的有穷自动机
确定的有穷自动机(Deterministic Finite Automata, DFA),有且只有一条离开该状态、以该符号为标号的边
DFA是NFA的一个特例,其中
δ
:
Q
×
Σ
↦
Q
\delta: Q \times \Sigma \mapsto Q
δ:Q×Σ↦Q
即:
1)没有输入
ϵ
\epsilon
ϵ之上的转换动作
2)对每个状态
s
s
s和每个输入符号
a
a
a,有且只有一条标号为
a
a
a的边离开
s
s
s
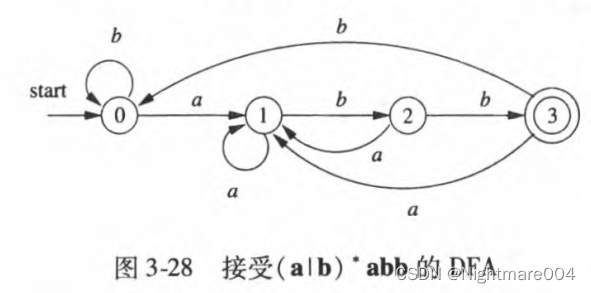
自动机中输入字符串的接受
一个NFA接受输入字符串 x x x,当且仅当对应的转换图中存在一条从开始状态到某个接收状态的路径,使得该路径中各条边上的标号祖传符号串 x x x(路径中的 ϵ \epsilon ϵ标号将被忽略)
正则表达式转NFA
McNaughton–Yamada–Thompson algorithm算法
**输入:**字母表
Σ
\Sigma
Σ上的一个正则表达式
r
\mathbf{r}
r
**输出:**一个接受
L
(
r
)
L\left(\mathbf{r}\right)
L(r)的
N
F
A
N
NFA\ N
NFA N
**方法:**首先对
r
\mathbf{r}
r进行语法分析,分解出组成它的子表达式。
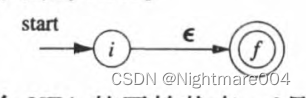
**基本规则:**对于表达式
ϵ
\mathbf{\epsilon}
ϵ,构造下面的
N
F
A
NFA
NFA
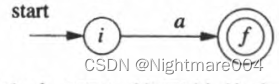
对于字母表
Σ
\Sigma
Σ中的子表达式
a
\mathbf{a}
a,构造下面的
N
F
A
NFA
NFA
**归纳规则:**假设正则表达式
s
\mathbf{s}
s和
t
\mathbf{t}
t的
N
F
A
NFA
NFA分别为
N
(
s
)
N\left(\mathbf{s}\right)
N(s)和
N
(
t
)
N\left(\mathbf{t}\right)
N(t)
1)假设
r
=
s
∣
t
\mathbf{r}=\mathbf{s}|\mathbf{t}
r=s∣t则如图构造
N
(
r
)
N\left(\mathbf{r}\right)
N(r)
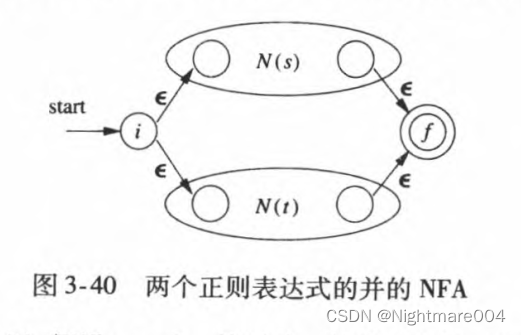
2)假设
r
=
s
t
\mathbf{r}=\mathbf{s}\mathbf{t}
r=st则如图构造
N
(
r
)
N\left(\mathbf{r}\right)
N(r)
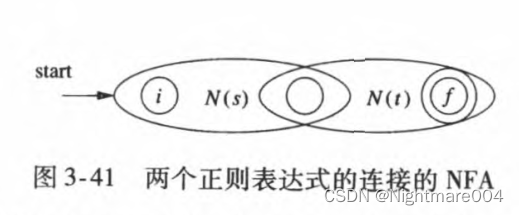
3)假设
r
=
s
∗
\mathbf{r}=\mathbf{s}^*
r=s∗则如图构造
N
(
r
)
N\left(\mathbf{r}\right)
N(r)
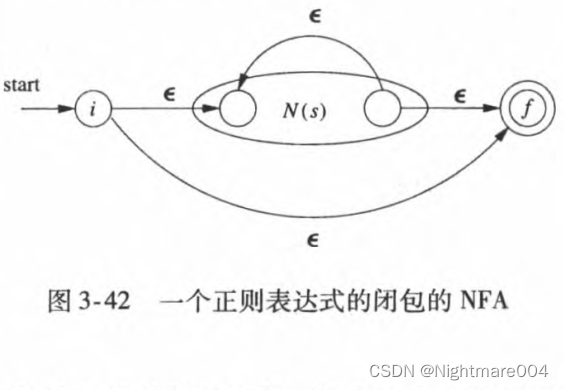
(不过我上课教的是下面这种
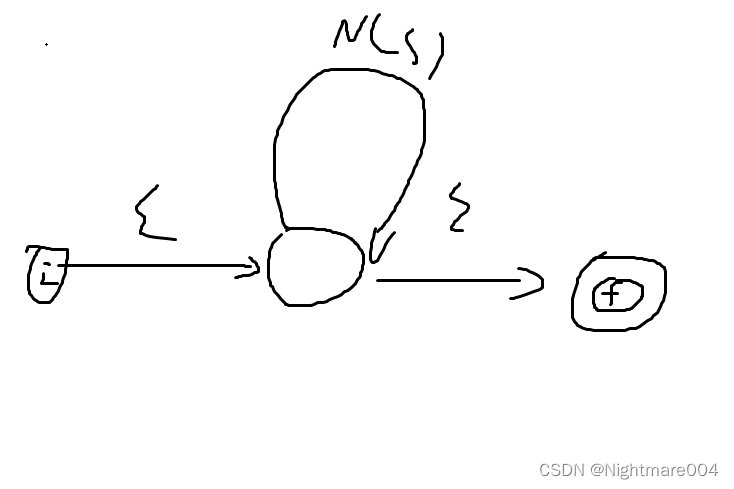
只是代码可能不好写)
4)假设
r
=
(
s
)
\mathbf{r}=\left(\mathbf{s}\right)
r=(s),那么
N
(
s
)
=
N
(
r
)
N\left(\mathbf{s}\right)=N\left(\mathbf{r}\right)
N(s)=N(r)
性质:
1)
N
(
r
)
N\left(\mathbf{r}\right)
N(r)状态数最多为
r
\mathbf{r}
r中的运算符和运算分量的总数的2倍(因为每一步构造最多多2个状态)
2)
N
(
r
)
N\left(\mathbf{r}\right)
N(r)有且有只有一个开始状态和一个接受状态。接受状态没有出边,开始状态没有入边
3)
N
(
r
)
N\left(\mathbf{r}\right)
N(r)除接受状态之外,每个状态要么有一条标号为
Σ
\Sigma
Σ中符号的出边,有么有两条标号为
ϵ
\epsilon
ϵ的出边(?)
代码
Trans.h
#pragma once
extern char const EPSILON = '$';
class Trans {
public:
int vertex_from;
int vertex_to;
char trans_symbol;
Trans(int vertex_from = 0, int vertex_to = 1, char trans_symbol = EPSILON) :
vertex_from(vertex_from), vertex_to(vertex_to), trans_symbol(trans_symbol) {}
};
NFA.h
这里没定义
Σ
\Sigma
Σ你可以自己写一下
默认0是起始状态
其他的都是一些get和set
#pragma once
#include"Trans.h"
#include<iostream>
#include<vector>
#include<stack>
#include<unordered_set>
class NFA {
public:
//0 is the only start state
int vertex_cnt;//Q
std::vector<Trans> transitions;//delta,transition graph
std::unordered_set<int> final_states;//F
NFA(int vertex_cnt = 0) :vertex_cnt(vertex_cnt) {}
NFA(int vertex_cnt, const std::vector<Trans>& transitions, const std::unordered_set<int>& final_states) :
vertex_cnt(vertex_cnt), transitions(transitions), final_states(final_states) {}
int get_vertex_count()const {
return vertex_cnt;
}
void set_vertex_cnt(int vertex_cnt) {
this->vertex_cnt = vertex_cnt;
}
std::vector<Trans> get_transition()const {
return transitions;
}
void add_transition(int vertex_from, int vertex_to, char trans_symbol) {
transitions.emplace_back(vertex_from, vertex_to, trans_symbol);
}
std::unordered_set<int> get_final_states()const {
return final_states;
}
void add_final_state(int state) {
final_states.insert(state);
}
void clear() {
vertex_cnt = 0;
transitions.clear();
final_states.clear();
}
void display()const {
printf("-------------------------\n");
for (Trans temp : transitions) {
printf("q_%d -> q_%d: %c\n", temp.vertex_from, temp.vertex_to, temp.trans_symbol);
}
printf("\n");
printf("\n");
printf("final_states: ");
for (int f : final_states) {
printf("%d ", f);
}
printf("\n");
printf("-------------------------\n");
}
};
Re2NFA.h
主要就是类似中缀表达式那样解析,碰到
∗
*
∗要立即结算
#pragma once
#include<iostream>
#include<string>
#include<stack>
#include<cctype>
#include"Trans.h"
#include"NFA.h"
//re: a.b
NFA concat(NFA a, NFA b) {
int a_vertex_cnt = a.get_vertex_count();
int b_vertex_cnt = b.get_vertex_count();
int total_states = a_vertex_cnt + b_vertex_cnt;
NFA result(total_states, a.get_transition(), { total_states - 1 });
result.add_transition(a_vertex_cnt - 1, a_vertex_cnt, EPSILON);
for (const Trans& trans : b.get_transition()) {
result.add_transition(
trans.vertex_from + a_vertex_cnt,
trans.vertex_to + a_vertex_cnt,
trans.trans_symbol);
}
return result;
}
//re: a*
NFA kleene(NFA a) {
int a_vertex_cnt = a.get_vertex_count();
NFA result(
a_vertex_cnt + 2, {
Trans(0,1,EPSILON),
Trans(a_vertex_cnt,1,EPSILON),
Trans(a_vertex_cnt,a_vertex_cnt + 1,EPSILON),
Trans(0,a_vertex_cnt + 1,EPSILON)
},
{ a_vertex_cnt + 1 }
);
for (const Trans& trans : a.get_transition()) {
result.add_transition(trans.vertex_from + 1, trans.vertex_to + 1, trans.trans_symbol);
}
return result;
}
//re: a|b
NFA or_selection(NFA a, NFA b) {
int a_vertex_cnt = a.get_vertex_count();
int b_vertex_cnt = b.get_vertex_count();
NFA result(
a_vertex_cnt + b_vertex_cnt + 2, {
Trans(0,1,EPSILON),
Trans(0,a_vertex_cnt + 1,EPSILON),
Trans(a_vertex_cnt,a_vertex_cnt + b_vertex_cnt + 1,EPSILON),
Trans(a_vertex_cnt + b_vertex_cnt,a_vertex_cnt + b_vertex_cnt + 1,EPSILON)
},
{ a_vertex_cnt + b_vertex_cnt + 1 }
);
for (const Trans& trans : a.get_transition()) {
result.add_transition(trans.vertex_from + 1, trans.vertex_to + 1, trans.trans_symbol);
}
for (const Trans& trans : b.get_transition()) {
result.add_transition(trans.vertex_from + a_vertex_cnt + 1, trans.vertex_to + a_vertex_cnt + 1, trans.trans_symbol);
}
return result;
}
int level(const char& op) {
if (op == '#') {
return 0;
}
else if (op == '(' || op == ')') {
return 1;
}
else if (op == '|') {
return 2;
}
//.
return 3;
}
/**
* compare right operator with left operator
* @param left_operator left operator
* @param right_operator right operator
* @return right operator>left operator return 1,= return 0,< -1
*/
int cmp(const char& left_operator, const char& right_operator) {
if (left_operator == '(' && right_operator == ')') {
return 0;
}
else if (right_operator == '(') {
return 1;
}
if (level(left_operator) < level(right_operator)) {
return 1;
}
return -1;
}
bool is_operator(const char& op) {
return op == '|' || op == '.' || op == '*' || op == '(' || op == ')';
}
NFA calculate(const NFA& left_operand, const NFA& right_operand, const char& op) {
if (op == '|') {
return or_selection(left_operand, right_operand);
}
return concat(left_operand, right_operand);
}
//McNaughton–Yamada–Thompson algorithm
NFA re2nfa(const std::string& expression) {
std::stack<NFA> operands;
std::stack<char> operators;
operators.push('#');
for (std::string::const_iterator it = expression.begin(); it != expression.end(); ++it) {
while (it != expression.end() && isspace(*it)) {
++it;
}
if (it == expression.end()) {
break;
}
char right_op = *it;
if (is_operator(right_op)) {
if (right_op == '*') {
NFA temp = operands.top();
operands.pop();
operands.push(kleene(temp));
}
else {
char left_op = operators.top();
int cmp_result = cmp(left_op, right_op);
//left_op >= right_op
while (cmp_result != 1) {
//left_op=='(' && right_op== ')'
if (cmp_result == 0) {
operators.pop();
break;
}
else {
NFA right_nfa = operands.top();
operands.pop();
NFA left_nfa = operands.top();
operands.pop();
operands.push(calculate(left_nfa, right_nfa, left_op));
operators.pop();
left_op = operators.top();
cmp_result = cmp(left_op, right_op);
}
}
if (right_op != ')') {
operators.push(right_op);
}
}
}
else {
operands.push(NFA(2, { Trans(0,1,*it) }, { 1 }));
}
}
char op = operators.top();
while (op != '#') {
operators.pop();
NFA right_nfa = operands.top();
operands.pop();
if (op == '*') {
operands.push(kleene(right_nfa));
}
else {
NFA left_nfa = operands.top();
operands.pop();
operands.push(calculate(left_nfa, right_nfa, op));
}
op = operators.top();
}
return operands.top();
}
NFA转DFA
子集构造法(subset construction)
输入:
N
F
A
N
=
(
Q
,
Σ
,
δ
,
q
0
,
F
)
NFA\ N=\left(Q,\Sigma,\delta,q_0,F\right)
NFA N=(Q,Σ,δ,q0,F)
输出:
D
F
A
D
=
(
Q
′
,
Σ
,
δ
′
,
q
0
′
,
F
′
)
DFA\ D=\left(Q',\Sigma,\delta',q_0',F'\right)
DFA D=(Q′,Σ,δ′,q0′,F′)
其中
Q
′
=
P
(
Q
)
,
q
0
′
=
ϵ
−
c
l
o
s
u
r
e
(
q
0
)
,
F
′
=
{
q
′
∈
Q
′
∣
q
′
∩
F
≠
∅
}
Q'=\mathcal{P}\left(Q\right),q_0'=\epsilon-closure\left(q_0\right),F'=\left\{q'\in Q'|q'\cap F\neq \empty\right\}
Q′=P(Q),q0′=ϵ−closure(q0),F′={q′∈Q′∣q′∩F=∅}
方法: 我们的算法为
D
D
D构造一个转换表
D
t
r
a
n
Dtran
Dtran。
D
D
D的每一个状态时一个
N
F
A
NFA
NFA状态的集合,
我们将构造
D
t
r
a
n
Dtran
Dtran,使得
D
D
D能够并行地模拟
N
N
N在遇到一个给定串时可能执行的所有动作。
定义如下操作
| 操作 | 描述 |
|---|---|
| ϵ − c l o s u r e ( s ) \epsilon-closure\left(s\right) ϵ−closure(s) | 能够从 N F A NFA NFA的状态 s s s开始只通过 ϵ \epsilon ϵ转换到达的 N F A NFA NFA状态合集 |
| ϵ − c l o s u r e ( T ) \epsilon-closure\left(T\right) ϵ−closure(T) | 能够从 T T T中某个 N F A NFA NFA的状态 s s s开始只通过 ϵ \epsilon ϵ转换道道的NFA状态集合,即 ⋃ s ∈ T ϵ − c l o s u r e ( s ) \bigcup\limits_{s\in T}\epsilon-closure\left(s\right) s∈T⋃ϵ−closure(s) |
| m o v e ( T , a ) move\left(T,a\right) move(T,a) | 能够从 T T T中某个状态 s s s出发通过标号为a的转换到达的 N F A NFA NFA状态的集合 |
我们必须找到当 N N N读入某个输入串之后可能位于的所有状态集合。
1)首先读入第一个输入符号之前,N可以位于集合
ϵ
−
c
l
o
s
u
r
e
(
s
0
)
\epsilon-closure\left(s_0\right)
ϵ−closure(s0)中的任何状态上,其中
s
0
s_0
s0时
N
N
N的开始状态
2)下面进行归纳,假定
N
N
N在读入输入串
x
x
x之后,可以位于集合
T
T
T中的状态上。
如果下一个输入符号是
a
a
a,那么
N
N
N可以立即移动到集合
m
o
v
e
(
T
,
a
)
move\left(T,a\right)
move(T,a)中的任何状态。
然而,
N
N
N可以在读入
a
a
a后,再执行几个
ϵ
\epsilon
ϵ转换,因此
N
N
N在读入
x
a
xa
xa后可能位于
ϵ
−
c
l
o
s
u
r
e
(
m
o
v
e
(
T
,
a
)
)
\epsilon-closure\left(move\left(T,a\right)\right)
ϵ−closure(move(T,a))中的任何状态上
子集构造法伪代码如下
Dstates={epsilon-closure(s_0)}; //epsilon-closure(s_0) is unmarked
for(T in Dstates){
mark T;
for(a in Sigma){//Sigma is the input alphabet
U=epsilon-closure(move(T,a));
if(U not in Dstates){
Dstates.add(U);//U is unmarked
}
Dtran[T,a]=U;
}
}
ϵ − c l o s u r e ( T ) \epsilon-closure\left(T\right) ϵ−closure(T)伪代码如下
//push all states in T to the stack
for(t in T){
statck.push(t);
}
epsilon-closure(T)=T;
while(!stack.empty()){
t = stack.top();
stack.pop();
for((t,epsilon,u) in delta){ //t can move to u by epsilon
if(u not in epsilon-closure(T)){
epsilon-clousre(T).add(u);
stack.push(u);
}
}
最终构造的转换表

最后,DFA所代表的状态集合,包含原来NFA的终态的,作为DFA的终态
有效性证明
N
F
A
N
=
(
Q
,
Σ
,
δ
,
q
0
,
F
)
NFA\ N=\left(Q,\Sigma,\delta,q_0,F\right)
NFA N=(Q,Σ,δ,q0,F)
D
F
A
D
=
(
Q
′
,
Σ
,
δ
′
,
q
0
′
,
F
′
)
DFA\ D=\left(Q',\Sigma,\delta',q_0',F'\right)
DFA D=(Q′,Σ,δ′,q0′,F′)
其中
Q
′
=
P
(
Q
)
,
q
0
′
=
ϵ
−
c
l
o
s
u
r
e
(
q
0
)
,
F
′
=
{
q
′
∈
Q
′
∣
q
′
∩
F
≠
∅
}
Q'=\mathcal{P}\left(Q\right),q_0'=\epsilon-closure\left(q_0\right),F'=\left\{q'\in Q'|q'\cap F\neq \empty\right\}
Q′=P(Q),q0′=ϵ−closure(q0),F′={q′∈Q′∣q′∩F=∅}
假设 w ∈ Σ ∗ w\in \Sigma^* w∈Σ∗,我们要证明 w ∈ L ( N ) ⇔ L ( N ) w\in L(N)\Leftrightarrow L(N) w∈L(N)⇔L(N)
实际上可以证明,假设
q
,
p
∈
Q
q,p\in Q
q,p∈Q,
N
N
N中存在从
q
q
q到
p
p
p的路径表示
w
w
w,当且仅当
D
D
D中存在从
ϵ
−
c
l
o
s
u
r
e
(
q
)
\epsilon-closure(q)
ϵ−closure(q)到P的路径表示
w
w
w(
p
∈
P
p\in P
p∈P)
证明:
用数学归纳法,
当
w
=
ϵ
w=\epsilon
w=ϵ时,
D
D
D只能直接接受
ϵ
\epsilon
ϵ,即
P
=
ϵ
−
c
l
o
s
u
r
e
(
q
)
P=\epsilon-closure(q)
P=ϵ−closure(q)
而
N
N
N,路径只能包含
ϵ
\epsilon
ϵ,即
p
∈
ϵ
−
c
l
o
s
u
r
e
(
q
)
=
P
p\in\epsilon-closure(q)=P
p∈ϵ−closure(q)=P
假设 ∣ w ∣ ≤ k \left|w\right|\le k ∣w∣≤k时成立(字符串 w w w长度小于等于 k k k)
当 ∣ w ∣ = k + 1 \left|w\right|=k+1 ∣w∣=k+1时,设 w = v a , ∣ v ∣ = k w=va,\left|v\right|=k w=va,∣v∣=k,且 v ∈ Σ ∗ , a ∈ Σ v\in \Sigma^*,a\in\Sigma v∈Σ∗,a∈Σ
如图
假设
N
N
N中存在从
q
q
q到
p
p
p的路径表示
w
w
w
这条路径可以表示为,
q
q
q存在路径表示
v
v
v,到达
r
1
r_1
r1,经过
a
a
a,到达
r
2
r_2
r2,再经过
ϵ
∗
\epsilon^*
ϵ∗到达
p
p
p
那么由归纳,
P
P
P中存在从
E
(
q
)
E(q)
E(q)到
R
R
R表示
v
v
v的路径
r
2
∈
m
o
v
e
(
R
,
a
)
,
p
∈
ϵ
−
c
l
o
s
u
r
e
(
m
o
v
e
(
R
,
a
)
)
r_2\in move(R,a),p \in \epsilon-closure\left(move(R,a)\right)
r2∈move(R,a),p∈ϵ−closure(move(R,a)),令
P
=
ϵ
−
c
l
o
s
u
r
e
(
m
o
v
e
(
R
,
a
)
)
P=\epsilon-closure\left(move(R,a)\right)
P=ϵ−closure(move(R,a)),就可以表示
w
w
w了
假设
D
D
D中存在从
ϵ
−
c
l
o
s
u
r
e
(
q
)
\epsilon-closure(q)
ϵ−closure(q)到P的路径表示
w
w
w,同样的
N
N
N中存在从
q
q
q到
p
p
p的路径表示
w
w
w
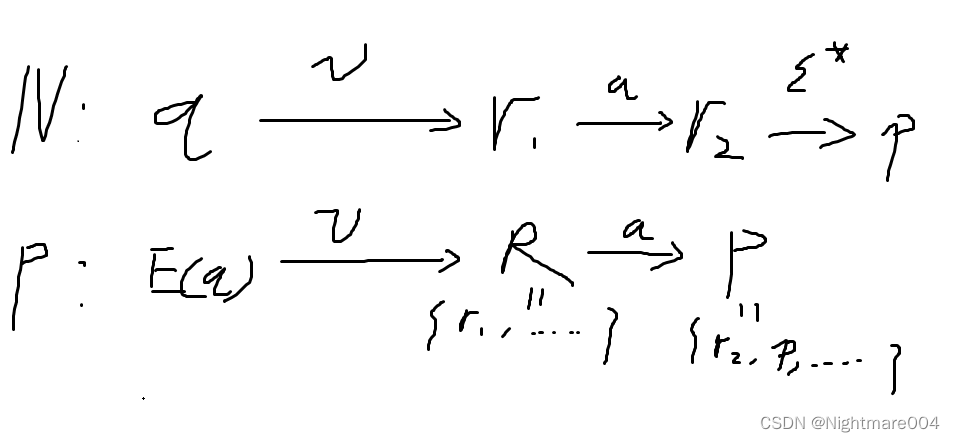
代码
NFA.h
与上面不同的是,多了
ϵ
−
c
l
o
s
u
r
e
(
T
)
,
m
o
v
e
(
T
,
a
)
\epsilon-closure(T),move(T,a)
ϵ−closure(T),move(T,a)
还写了个find_traverse_symbols,因为我没有定义
Σ
\Sigma
Σ,所以需要找到所有的边上的字符
#pragma once
#include"Trans.h"
#include<iostream>
#include<vector>
#include<stack>
#include<unordered_set>
class NFA {
public:
//0 is the only start state
int vertex_cnt;//Q
std::vector<Trans> transitions;//delta,transition graph
std::unordered_set<int> final_states;//F
NFA(int vertex_cnt = 0) :vertex_cnt(vertex_cnt) {}
NFA(int vertex_cnt, const std::vector<Trans>& transitions, const std::unordered_set<int>& final_states) :
vertex_cnt(vertex_cnt), transitions(transitions), final_states(final_states) {}
int get_vertex_count()const {
return vertex_cnt;
}
void set_vertex_cnt(int vertex_cnt) {
this->vertex_cnt = vertex_cnt;
}
std::vector<Trans> get_transition()const {
return transitions;
}
void add_transition(int vertex_from, int vertex_to, char trans_symbol) {
transitions.emplace_back(vertex_from, vertex_to, trans_symbol);
}
std::unordered_set<int> get_final_states()const {
return final_states;
}
void add_final_state(int state) {
final_states.insert(state);
}
void clear() {
vertex_cnt = 0;
transitions.clear();
final_states.clear();
}
void display()const {
printf("-------------------------\n");
for (Trans temp : transitions) {
printf("q_%d -> q_%d: %c\n", temp.vertex_from, temp.vertex_to, temp.trans_symbol);
}
printf("\n");
printf("\n");
printf("final_states: ");
for (int f : final_states) {
printf("%d ", f);
}
printf("\n");
printf("-------------------------\n");
}
std::unordered_set<int> epsilon_closure(const std::unordered_set<int>& T)const {
std::stack<int> st;
for (const int& state : T) {
st.push(state);
}
std::unordered_set<int> closure = T;
while (!st.empty()) {
int t = st.top();
st.pop();
for (const Trans& trans : transitions) {
if (trans.trans_symbol == EPSILON &&
closure.find(trans.vertex_from) != closure.end() &&
closure.find(trans.vertex_to) == closure.end()) {
closure.insert(trans.vertex_to);
st.push(trans.vertex_to);
}
}
}
return closure;
}
std::unordered_set<int> move_symbol(const std::unordered_set<int>& T, const char& symbol)const {
std::unordered_set<int> result;
for (const int& state : T) {
for (const Trans& trans : transitions) {
if (trans.vertex_from == state && trans.trans_symbol == symbol) {
result.insert(trans.vertex_to);
}
}
}
return result;
}
//u in states, (u,symbol,t) in transition, result={all symbol}
std::unordered_set<char> find_traverse_symbols(const std::unordered_set<int>& states)const {
std::unordered_set<char> result;
for (const int& state : states) {
for (const Trans& trans : transitions) {
if (trans.vertex_from == state && trans.trans_symbol != EPSILON) {
result.insert(trans.trans_symbol);
}
}
}
return result;
}
};
DFA.h
这里的转换函数,用的是邻接表
起始状态也是0
#pragma once
#include<vector>
#include<stack>
#include<unordered_map>
#include<unordered_set>
class DFA {
public:
//0 is the only start state
int vertex_cnt;//Q
std::vector<std::unordered_map<char, int> > transitions;//delta,transition graph
std::unordered_set<int> final_states;//F
DFA(int vertex_cnt = 0) :vertex_cnt(vertex_cnt) {}
DFA(int vertex_cnt, const std::vector<std::unordered_map<char, int> >& transitions, const std::unordered_set<int>& final_states) :
vertex_cnt(vertex_cnt), transitions(transitions), final_states(final_states) {}
int get_vertex_cnt()const {
return vertex_cnt;
}
std::vector<std::unordered_map<char, int> > get_transitions()const {
return transitions;
}
std::unordered_set<int> get_final_states()const {
return final_states;
}
void display()const {
printf("-------------------------\n");
for (int i = 0; i < transitions.size(); ++i) {
for (const auto& temp : transitions[i]) {
printf("q_%d -> q_%d: %c\n", i, temp.second, temp.first);
}
}
printf("\n");
printf("\n");
printf("final_states: ");
for (int f : final_states) {
printf("%d ", f);
}
printf("\n");
printf("-------------------------\n");
}
};
NFA2DFA.h
#pragma once
#include<vector>
#include<unordered_set>
#include<unordered_map>
#include<queue>
#include"Trans.h"
#include"NFA.h"
#include"DFA.h"
//subset construction
DFA nfa2dfa(const NFA& nfa) {
std::vector<std::unordered_set<int> > idx2state;
std::vector<std::unordered_map<char, int> > transitions;
std::queue<int> q;
q.push(0);
idx2state.push_back(nfa.epsilon_closure({ 0 }));
transitions.emplace_back(std::unordered_map<char, int>());
while (!q.empty()) {
int cur = q.front();
q.pop();
//for(a in Sigma)
for (const char& symbol : nfa.find_traverse_symbols(idx2state[cur])) {
std::unordered_set<int> temp = nfa.epsilon_closure(nfa.move_symbol(idx2state[cur], symbol));
int i = 0;
while (i < idx2state.size()) {
if (idx2state[i] == temp) {
break;
}
++i;
}
//mark unseen state
if (i == idx2state.size()) {
q.push(i);
idx2state.emplace_back(temp);
transitions.emplace_back(std::unordered_map<char, int>());
}
transitions[cur][symbol] = i;
}
}
std::unordered_set<int> F = nfa.get_final_states();
std::unordered_set<int> final_states;
for (int i = 0; i < idx2state.size(); ++i) {
for (const int& state : idx2state[i]) {
//set which contains final is a final set
if (F.find(state) != F.end()) {
final_states.insert(i);
break;
}
}
}
return DFA(transitions.size(), transitions, final_states);
}
NFA转正则表达式
Kleene’s algorithm
GNFA:与NFA类似,但是边是正则表达式
第一步:创建一个唯一的开始状态和接受状态
开始状态用
ϵ
\epsilon
ϵ连接原来的开始状态
所有接受状态用
ϵ
\epsilon
ϵ连接新的接受状态
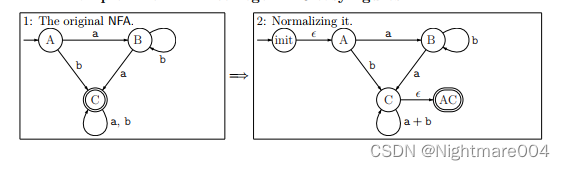
第二步:依次消除非初始状态和非接受状态
假设消除
S
2
S_2
S2
S
0
,
S
1
S_0,S_1
S0,S1到
S
2
S_2
S2有边
且
S
2
S_2
S2到
S
3
,
S
4
S_3,S_4
S3,S4有边
则产生4条边
S
0
→
S
3
S_0\to S_3
S0→S3,
S
0
→
S
4
S_0\to S_4
S0→S4,
S
1
→
S
3
S_1\to S_3
S1→S3,
S
1
→
S
4
S_1\to S_4
S1→S4,边上的正则表达式为原来的边的连接
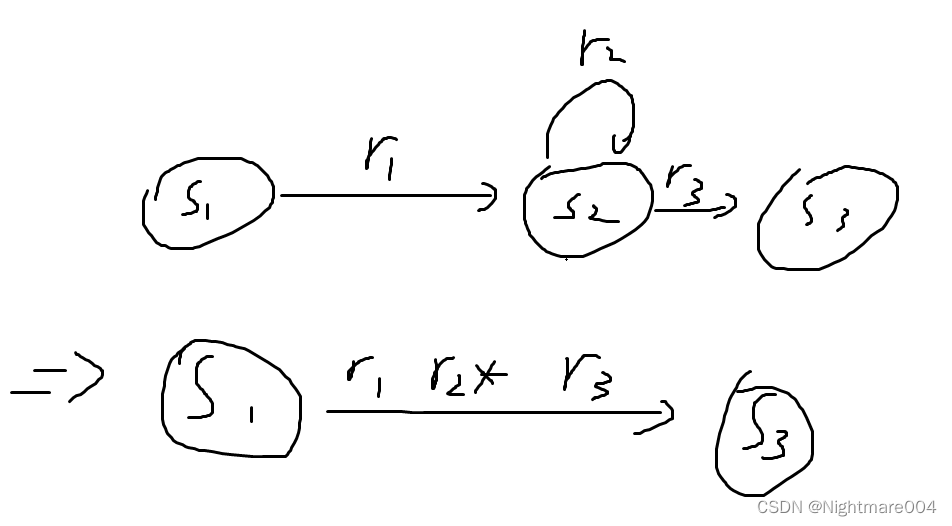
如果一个状态有2条边到另一个状态,则合并
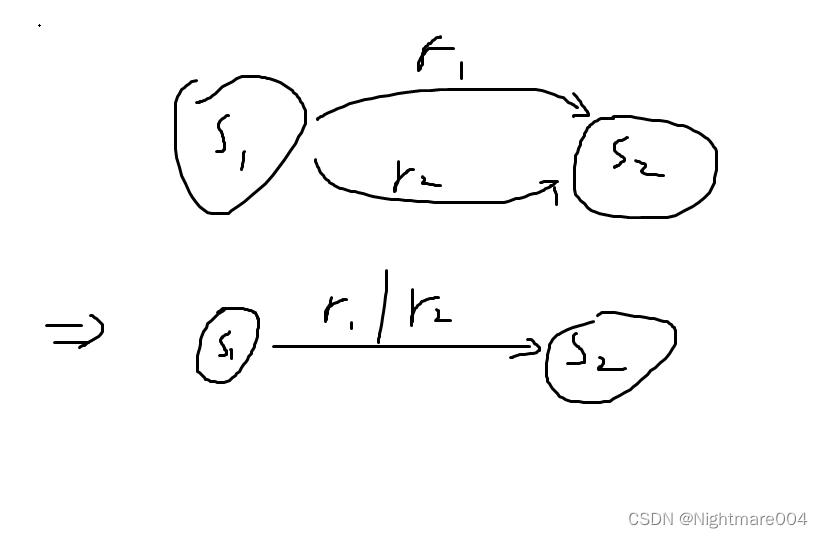
最后产生

最复杂的情况之一
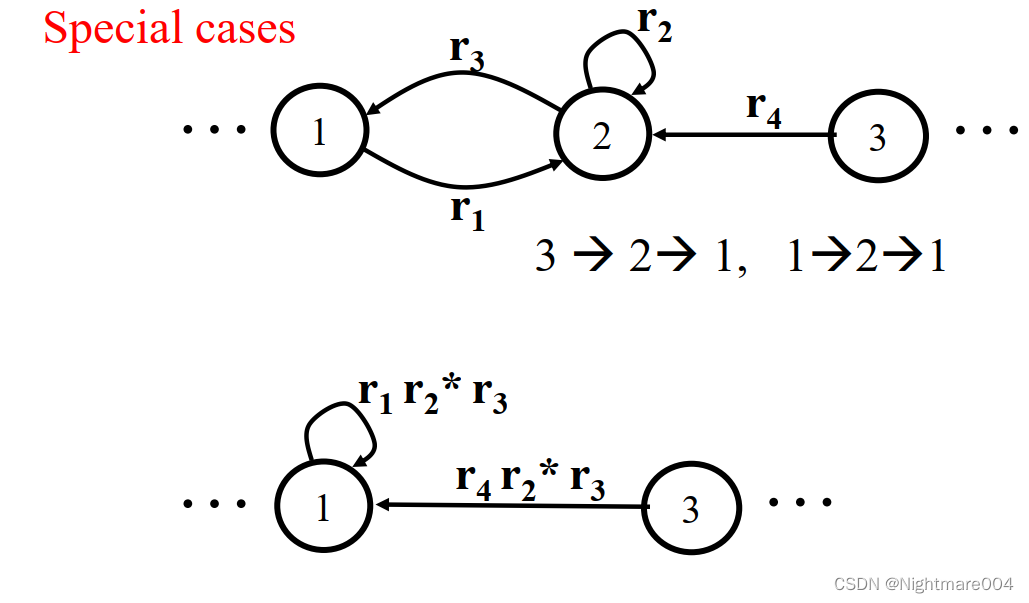
代码
再说
Kleene’s Theorem
正则语言等价于可以被有限状态自动机接受
证明:
正则语言转有限状态自动机:McNaughton–Yamada–Thompson algorithm算法
有限状态自动机转正则语言:Kleene’s algorithm
Myhill–Nerode theorem
可区分字符串
设
L
L
L是一个语言
x
,
y
∈
Σ
∗
x,y\in \Sigma^*
x,y∈Σ∗
如果
∃
z
\exists z
∃z使得
x
z
∈
L
,
y
z
∉
L
xz\in L,yz\notin L
xz∈L,yz∈/L,则称
x
,
y
x,y
x,y在
L
L
L上可区分(distinguishable to L)
引理1
设
L
L
L是一个语言,
D
F
A
M
DFA\ M
DFA M可以识别
L
L
L,
x
,
y
∈
Σ
∗
x,y\in \Sigma^*
x,y∈Σ∗在L上可区分
则
M
M
M输入
x
x
x到达的状态和输入
y
y
y到达的状态不同
证明:
假设
x
,
y
x,y
x,y到达的状态一样
则输入
x
z
,
y
z
xz,yz
xz,yz到达的状态也一样,
即
x
z
∈
L
xz\in L
xz∈L且
y
z
∈
L
yz \in L
yz∈L或者
x
z
∉
L
xz \notin L
xz∈/L且
y
z
∉
L
yz\notin L
yz∈/L,与
x
,
y
x,y
x,y在
L
L
L上可区分矛盾
可区分字符串集合
可区分字符串集合(Distinguishing Set of Strings)
设
L
L
L是一个语言,
S
=
{
x
1
,
⋯
,
x
k
}
S=\left\{x_1,\cdots,x_k\right\}
S={x1,⋯,xk}
如果
∀
x
i
,
x
j
∈
S
,
x
i
≠
x
j
\forall x_i,x_j\in S, x_i\neq x_j
∀xi,xj∈S,xi=xj,则
S
S
S是L上的可区分字符串集合
引理2
设
L
⊆
Σ
∗
L\subseteq \Sigma^*
L⊆Σ∗是任意语言,
S
S
S是
L
L
L上的可区分字符串集合
则识别
L
L
L的
D
F
A
DFA
DFA至少有
∣
S
∣
\left|S\right|
∣S∣个状态
证明:
设
S
=
{
x
1
,
⋯
,
x
k
}
S=\left\{x_1,\cdots,x_k\right\}
S={x1,⋯,xk}
根据Kleene’s Theorem,对于非正则语言,不存在有限自动机识别,即状态数是无限的
如果
L
L
L是正则语言,设
D
F
A
M
DFA\ M
DFA M可以识别
L
L
L
∀
i
≠
j
\forall i\neq j
∀i=j,
x
i
,
x
j
x_i,x_j
xi,xj是可区分的,则根据引理1,输入
M
M
M,他们将到达不同状态,也就是说至少有
∣
S
∣
\left|S\right|
∣S∣个状态
定义:
≈
L
\approx_L
≈L, 如果
x
,
y
x,y
x,y在
L
L
L上不可区分,则
x
≈
L
y
x \approx_{L} y
x≈Ly,容易验证这是一个等价关系
有了等价关系就可以划分等价类,记为
[
x
]
\left[x\right]
[x]
引理2也可以写作识别正则语言
L
L
L的
D
F
A
DFA
DFA的状态数至少为等价类的数量
定理
L L L是正则语言当且仅当 L L L有有限个根据 ≈ L \approx_L ≈L划分等价类,并且 L L L可以被DFA识别,这个DFA的状态数为等价类的数量
证明:
现在要定义一个
D
F
A
M
DFA\ M
DFA M识别
L
L
L,并且状态数为等价类的数量
显然起始状态为
[
ϵ
]
\left[\epsilon\right]
[ϵ],接受状态为
[
x
]
(
x
∈
L
)
\left[x\right](x\in L)
[x](x∈L)
设
a
∈
Σ
a\in\Sigma
a∈Σ,定义
δ
(
[
x
]
,
a
)
=
[
x
a
]
\delta\left(\left[x\right],a\right)=\left[xa\right]
δ([x],a)=[xa],容易验证一个等价类的任意字符串,经过
a
a
a,会到达相同的状态
根据数学归纳法,容易验证
M
M
M可以识别
L
L
L
举个例子
(
a
∣
b
)
∗
b
b
b
(
a
∣
b
)
\left(a|b\right)^*bbb\left(a|b\right)
(a∣b)∗bbb(a∣b),可以划分为4个等价类
[
ϵ
]
,
[
b
]
,
[
b
b
]
,
[
b
b
b
]
[\epsilon],[b],[bb],[bbb]
[ϵ],[b],[bb],[bbb]
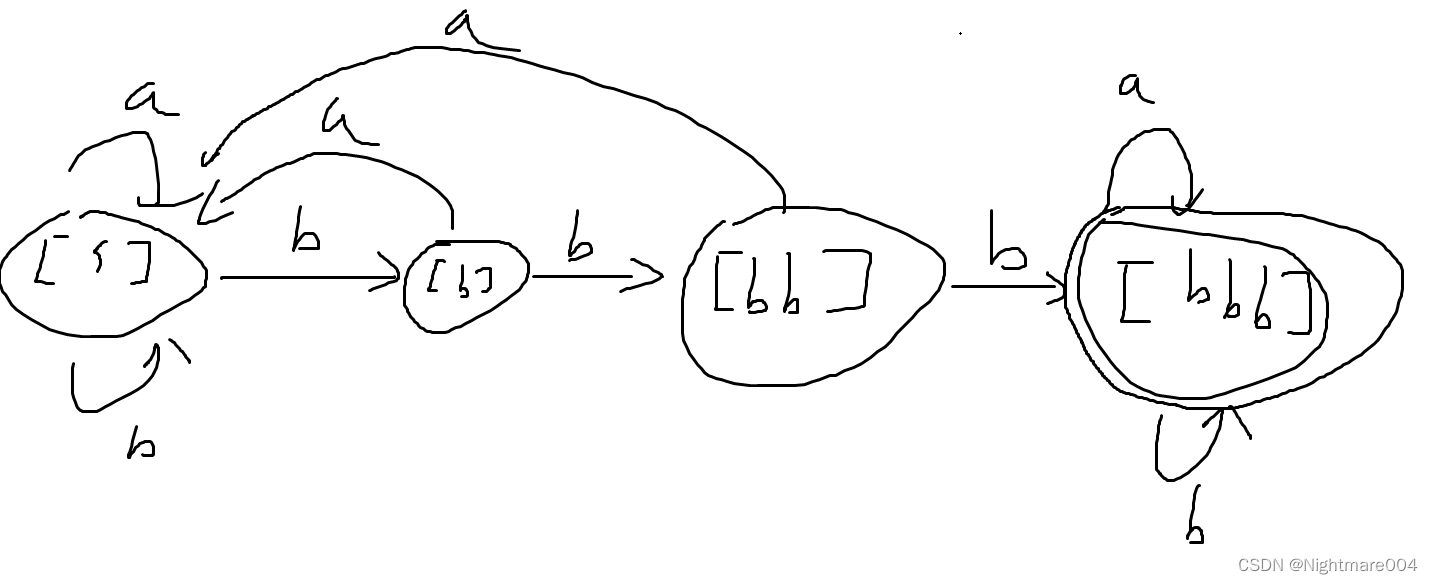
另一个例子
L
=
{
0
n
1
n
∣
n
≥
0
}
L=\left\{0^n 1^n|n\ge0\right\}
L={0n1n∣n≥0}不是正规语言,因为可以划分等价类
[
0
]
,
[
00
]
,
⋯
[0],[00],\cdots
[0],[00],⋯,有无穷个等价类,所以不是正则语言
(当然也可以用pumping lemma,不过并不是所有非正则语言都可以用pumping lemma验证)
DFA最小化
不可达状态:DFA在任意输入串下都无法到达的状态
等价状态/不可分状态(indistinguishable):同一输入串下不产生区别的状态
消除不可达状态
其实就是根据 Σ \Sigma Σ执行bfs
合并等价状态
Hopcroft算法
输入: 一个
D
F
A
D
DFA\ D
DFA D,其状态集合为
S
S
S,输入字母表为
Σ
\Sigma
Σ,开始状态为
s
0
s_0
s0,接受状态集为
F
F
F
输出: 一个
D
F
A
D
′
DFA\ D'
DFA D′,它和
D
D
D接受相同的语言,且状态最少
方法:
1)首先构造包含两个组
F
F
F和
S
−
F
S-F
S−F的初始划分
Π
\Pi
Π,这两个组分别是
D
D
D的接受状态组和非接受状态组
2)

3)如果
Π
n
e
w
=
Π
\Pi_{new}=\Pi
Πnew=Π,令
Π
f
i
n
a
l
=
Π
\Pi_{final}=\Pi
Πfinal=Π并接着执行步骤4;否则,用
Π
n
e
w
\Pi_{new}
Πnew替换
Π
\Pi
Π并重复步骤2
4)在分划
Π
f
i
n
a
l
\Pi_{final}
Πfinal的每个组中选取一个状态作为该组的代表,这些代表构成
D
′
D'
D′的状态
a)
D
′
D'
D′的开始状态是包含了
D
D
D的开始状态的组的代表
b)
D
′
D'
D′的接受状态是那些包含了
D
D
D的接受状态的组的代表
c)令
s
s
s是
Π
f
i
n
a
l
\Pi_{final}
Πfinal中某个组
G
G
G的代表,并令
D
F
A
D
DFA\ D
DFA D中在输入
a
a
a上离开
s
s
s的转换到达状态
t
t
t。
令
r
r
r为
t
t
t所在组
H
H
H的代表。那么在
D
′
D'
D′中存在一个从
s
s
s到
r
r
r在输入
a
a
a上的转换。
(其实4就是把原来的边拼上去而已)
伪代码

最小化DFA唯一证明
假设所有的状态都可以到达
设最小化
D
F
A
A
=
(
Q
A
,
Σ
,
δ
A
,
q
0
,
A
,
F
A
)
DFA\ A=\left(Q_{A},\Sigma,\delta_A,q_{0,A},F_A\right)
DFA A=(QA,Σ,δA,q0,A,FA)
以及最小化
D
F
A
B
=
(
Q
B
,
Σ
,
δ
B
,
q
0
,
B
,
F
B
)
DFA\ B=\left(Q_{B},\Sigma,\delta_B,q_{0,B},F_B\right)
DFA B=(QB,Σ,δB,q0,B,FB)
由最小化, ∣ Q A ∣ = ∣ Q B ∣ = k \left|Q_A\right|=\left|Q_B\right|=k ∣QA∣=∣QB∣=k
S
=
{
x
1
,
x
2
,
⋯
,
x
k
}
S=\left\{x_1,x_2,\cdots,x_k\right\}
S={x1,x2,⋯,xk}是
L
L
L上的可区分字符串集合
显然
δ
(
q
0
,
A
,
x
1
)
≠
δ
(
q
0
,
A
,
x
2
)
\delta\left(q_{0,A},x_1\right)\neq \delta\left(q_{0,A},x_2\right)
δ(q0,A,x1)=δ(q0,A,x2)
设
q
A
=
δ
(
q
0
,
A
,
x
1
)
,
q
B
=
δ
(
q
0
,
B
,
x
1
)
q_A=\delta\left(q_{0,A},x_1\right),q_{B}=\delta\left(q_{0,B},x_1\right)
qA=δ(q0,A,x1),qB=δ(q0,B,x1)
即
Q
A
Q_A
QA和
Q
B
Q_B
QB内的状态可以一一对应
q
A
=
δ
(
q
1
,
A
,
x
1
)
,
q
B
=
δ
(
q
1
,
B
,
x
1
)
q_A=\delta\left(q_{1,A},x_1\right),q_{B}=\delta\left(q_{1,B},x_1\right)
qA=δ(q1,A,x1),qB=δ(q1,B,x1)也应该一一对应(即边也是一样的
所以
A
=
B
A=B
A=B
代码
DFAMinimal.h
#pragma once
#include<vector>
#include<unordered_map>
#include<unordered_set>
#include<queue>
#include<vector>
#include<algorithm>
#include"DFA.h"
//bfs
DFA remove_unreachable_state(const DFA& dfa, const std::vector<char>& symbols) {
std::queue<int> q;
q.push(0);
std::unordered_set<int> reachable_state = { 0 };
int vertex_cnt = dfa.get_vertex_cnt();
std::vector<std::unordered_map<char, int> > transitions = dfa.get_transitions();
std::unordered_set<int> final_states = dfa.get_final_states();
while (!q.empty()) {
int cur = q.front();
q.pop();
std::unordered_map<char, int> temp = transitions[cur];
//traverse symbols (Sigma)
for (const char& c : symbols) {
if (temp.find(c) != temp.end()) {
int state = temp[c];
if (reachable_state.find(state) == reachable_state.end()) {
q.push(state);
reachable_state.insert(state);
}
}
}
}
std::vector<int> idx2state(vertex_cnt);
std::vector<std::unordered_map<char, int> > new_transitions;
std::unordered_set<int> new_final_states;
int cnt = 0;
//relabel and find new final states
for (int i = 0; i < vertex_cnt; ++i) {
if (reachable_state.find(i) != reachable_state.end()) {
idx2state[i] = cnt;
if (final_states.find(i) != final_states.end()) {
new_final_states.insert(cnt);
}
++cnt;
}
}
for (int i = 0; i < vertex_cnt; ++i) {
if (reachable_state.find(i) != reachable_state.end()) {
std::unordered_map<char, int> temp;
for (const auto& transition : transitions[i]) {
if (reachable_state.find(transition.second) != reachable_state.end()) {
temp[transition.first] = idx2state[transition.second];
}
}
new_transitions.push_back(temp);
}
}
return DFA(cnt, new_transitions, new_final_states);
}
DFA hopcroft(const DFA& dfa, const std::vector<char>& symbols) {
int vertex_cnt = dfa.get_vertex_cnt();
std::vector<std::unordered_map<char, int> > transitions = dfa.get_transitions();
std::unordered_set<int> final_states = dfa.get_final_states();
std::unordered_set<int> start_states;
for (int i = 0; i < vertex_cnt; ++i) {
if (final_states.find(i) == final_states.end()) {
start_states.insert(i);
}
}
std::vector<std::unordered_set<int> > partition = { start_states,final_states };//Q'
std::vector<std::unordered_set<int> > work_list = { final_states };//W
while (!work_list.empty()) {
std::unordered_set<int> q_prime = work_list.back();
work_list.pop_back();
for (const char& symbol : symbols) {
std::unordered_set<int> x;//predecessor
for (int i = 0; i < vertex_cnt; ++i) {
if (transitions[i].find(symbol) != transitions[i].end()&&
q_prime.find(transitions[i][symbol]) != q_prime.end()) {
x.insert(i);
}
}
if (!x.empty()) {
std::vector<std::unordered_set<int> > temp;
for (const auto& y : partition) {
std::unordered_set<int> y_cap_x;//y cap x
std::unordered_set<int> y_diff_x;//y-x
//split
for (const int& state : y) {
if (x.find(state) != x.end()) {
y_cap_x.insert(state);
}
else {
y_diff_x.insert(state);
}
}
if (!y_cap_x.empty() && !y_diff_x.empty()) {
temp.push_back(y_cap_x);
temp.push_back(y_diff_x);
auto it = std::find(work_list.begin(), work_list.end(), y);
if (it != work_list.end()) {
work_list.erase(it);
work_list.push_back(y_cap_x);
work_list.push_back(y_diff_x);
}
else if (y_cap_x.size() < y_diff_x.size()) {
work_list.push_back(y_cap_x);
}
else {
work_list.push_back(y_diff_x);
}
}
else {
//indistinguish, don't split y
temp.push_back(y);
}
}
partition = temp;
}
}
}
int cnt = partition.size();
//let the partition which contains 0 also be 0 in the new dfa
for (int i = 0; i < cnt; ++i) {
bool flag = false;
for (const int& state : partition[i]) {
if (state == 0) {
std::swap(partition[i], partition[0]);
flag = true;
break;
}
}
if (flag) {
break;
}
}
std::vector<std::unordered_map<char, int> > new_transitions(cnt);
std::unordered_set<int> new_final_states;
std::vector<int> idx2state(vertex_cnt);
//relabel and find new final states
for (int i = 0; i < cnt; ++i) {
for (const int& state : partition[i]) {
idx2state[state] = i;
if (final_states.find(state) != final_states.end()) {
new_final_states.insert(i);
}
}
}
for (int i = 0; i < transitions.size(); ++i) {
for (const auto& p : transitions[i]) {
new_transitions[idx2state[i]][p.first] = idx2state[p.second];
}
}
return DFA(cnt, new_transitions, new_final_states);
}
完整代码
https://github.com/Nightmare4214/re_nfa_dfa
参考
https://en.wikipedia.org/wiki/Regular_language
http://cgosorio.es/Seshat/thompsonForm
https://courses.cs.washington.edu/courses/cse322/01sp/subset.pdf
https://gist.github.com/fonlang/f712e1463bf276b389e27164b60bd023
https://www.omegaxyz.com/2019/02/01/hopcroft-min-dfa/
https://en.wikipedia.org/wiki/DFA_minimization
https://codeantenna.com/a/36ziXkYcjM
https://people.csail.mit.edu/rrw/6.045-2019/notemindfa.pdf
https://cse.sc.edu/~fenner/csce551/minimization.pdf
https://neuraldump.net/2017/11/proof-of-kleenes-theorem/
https://en.wikipedia.org/wiki/Kleene%27s_algorithm
https://inside.mines.edu/~ndantam/csci-561/L11-min-prelecture.pdf