2022年认证杯SPSSPRO杯数学建模

A题 人员的紧急疏散求解

原题再现：

  在过去的几十年里，由于大规模集会活动的数量和规模的增加，紧急疏散的问题变得越来越重要。通过有限宽度的门或狭窄通道进行疏散是最值得关注的情况之一。为了更好地理解各种情况下的人群行为，已经进行了许多实验和数值模拟。门的宽度、人群组成、出口的位置都会影响疏散的效果。组织真人进行实验固然是一种有效的方法，但由于环境和背景的真实性、压力水平、人员密度、样本大小等无法和真实情况一致，所以许多不同的研究结果都是有争议甚至是互相矛盾的。
  基于模型的研究不需要面对实验遇到的困难。但如果模型的假设是不可靠的，它们可能会产生与现实不符的结果。我们需要针对不同的情形和参数进行研究，来了解人群在疏散逃生时可能呈现出的不同动力学行为。
  第二阶段问题：
  1. 我们继续研究人的行为模式对疏散结局的影响。如果疏散的必经之路是一条狭窄通道，请对逃生者的行为模式建立合理的模型，研究在狭窄通道内发生踩踏事件的风险，给出影响踩踏风险的关键因素。并请指出如下因素将对踩踏风险有怎样的影响：
  (a) 通道宽度的改变；
  (b) 通道内的能见度和噪声。
  2. 客机在发生紧急情况时，机舱内的乘客需要进行快速撤离。客舱通道往往较为狭窄且不够通畅，而且此时由于乘客的慌乱，可能无法达成最理想的组织状态。这都给撤离行动的效率带来了挑战。请对乘客的自发行动模式建立合理的模型，研究其关键因素对撤离结果的影响。并对使用 3–4–3 布局的双通道客机机舱进行模拟计算。

整体求解过程概述(摘要)

  随着场景结构的愈加复杂，大规模集会数目与规模骤增，突发事件的频发，因此开展人群疏散与踩踏风险探究具有显著意义。
  采用合理的方法去找出影响人员疏散的关键因素和探讨分析是如何影响是非常有必要的。按照本题的要求，将分为三部分进行研究。1.建立模型分析人员在疏散时发生踩踏风险的影响因子 ，2. 通道宽度的改变, 能见度和噪声对踩踏风险的影响，3.人员密度、疏散门宽和能见度对疏散人员选择出口的影响。
  对于第一问首先通过第一阶段所得到的改进社会力模型的基础上为进一步探究关键因子对踩踏风险的摆控作用，引入了仿真模拟下的梯升树模型，模拟得到关键变量与风险的函数关系，建立了基于拐角点算法的有关变量导致效果的过程函数。
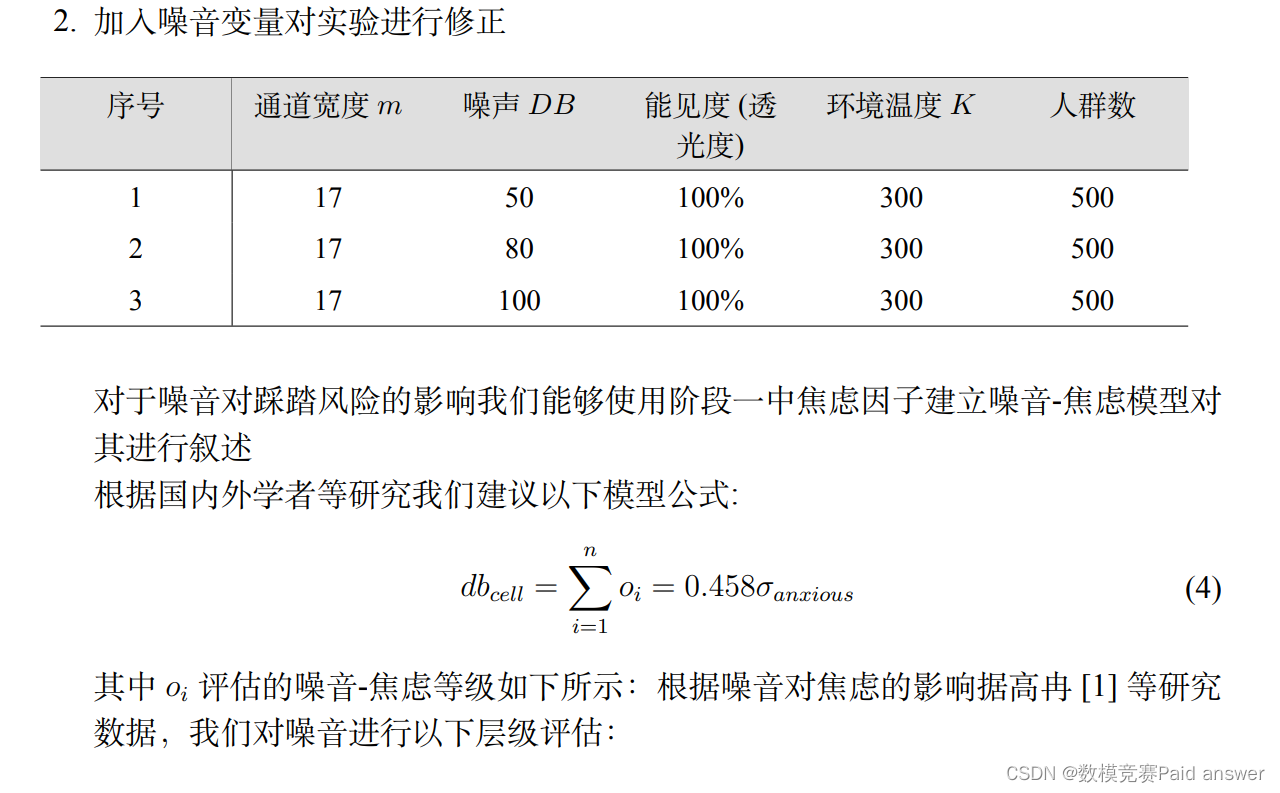
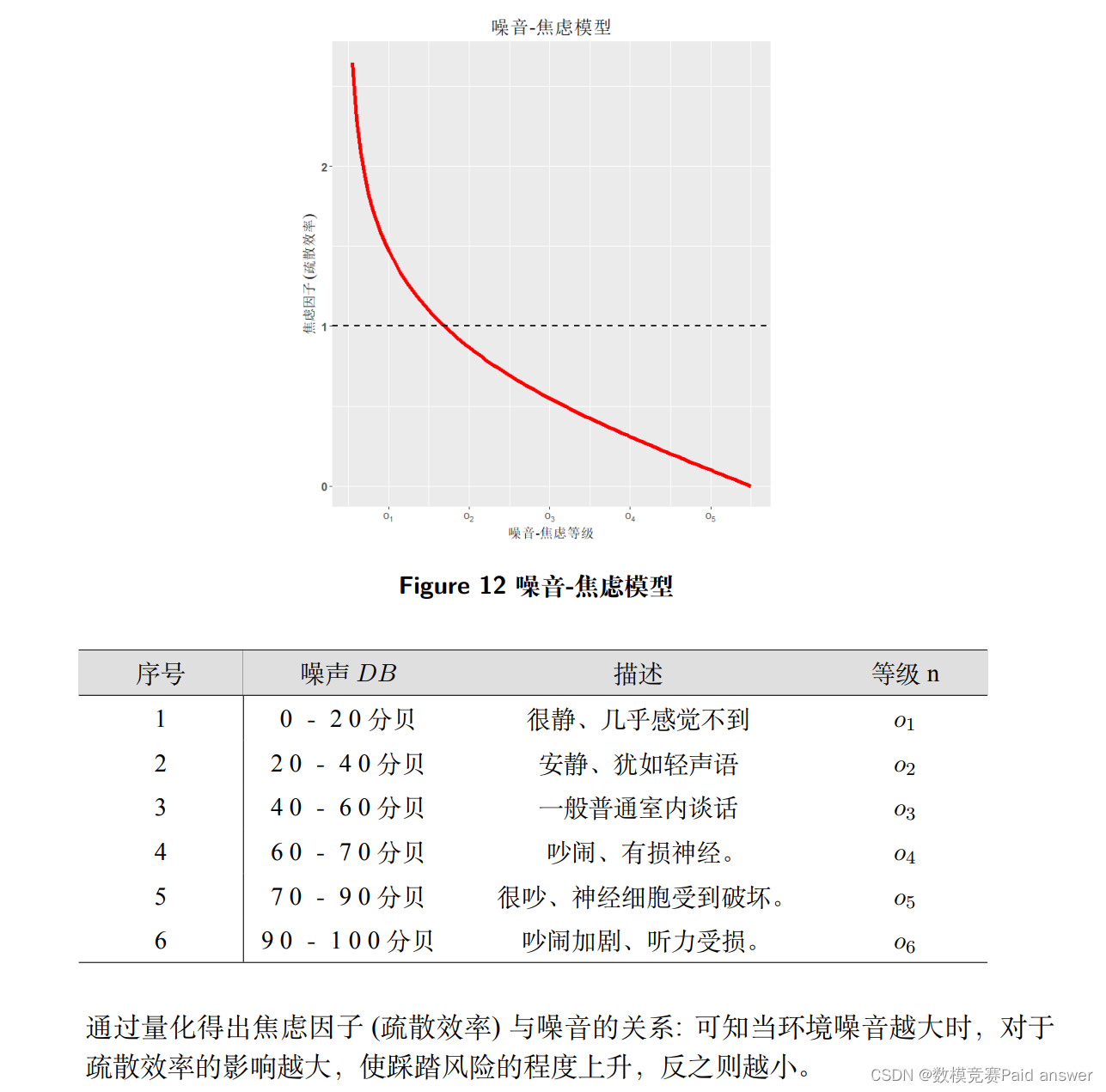
  其次，通过编写 FDS 与 Anylogic 来进行仿真模拟获得数据支持, 动态地更新仿真参数,分析得到能见度和疏散门宽对疏散速率（踩踏风险）的影响，得出以下结论：随着能见度的降低，人员疏散速率减缓。疏散通道的宽度变窄，踩踏风险因子升高，疏散人员在出口位置易发生集聚，导致疏散人员速率减缓，此外对噪声进行了等级评估，最终建立噪声-焦虑模型并对踩踏风险进行了分析，最终得出三个参数对踩踏风险的影响结果。
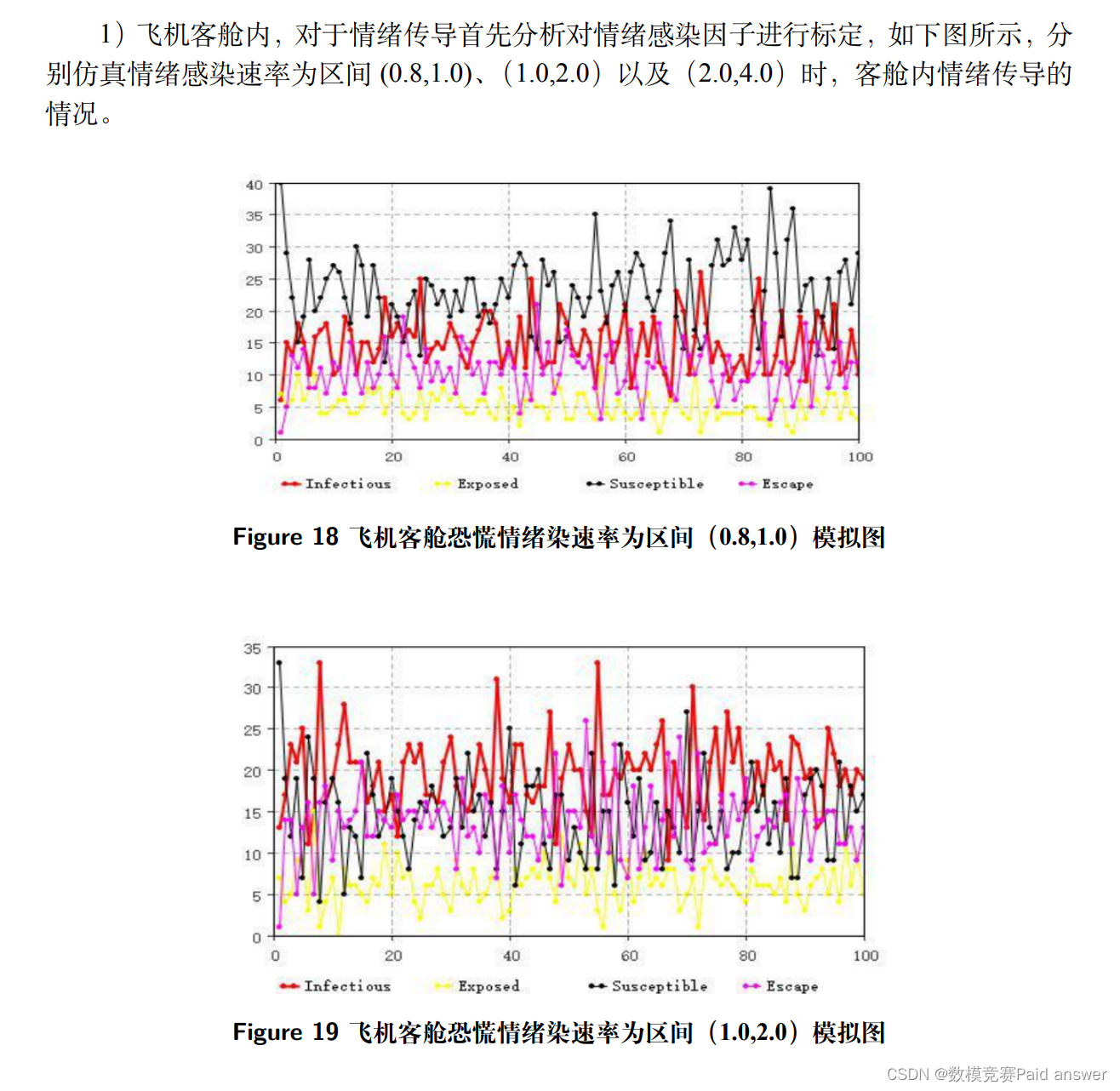
  针对第二问，本文考虑人群疏散的环境配置，基于行为性修正社会力模型对飞机客舱进行模拟，考虑到情绪传导，利用模拟仿真仪群算法，分析了恐慌情绪影响撤离速度，本文加入客舱场景的通行程度分类并构建初始导航网络，分析得到顾及关键因子对疏散速率变化情况图。针对双通道客机机舱仿真模拟实验，分析疏散行人的运动状态和受力情况，使得对整个疏散状态的瓶颈处以及疏散状态走向有较好的预测。
  此外，为保证此系统的仿真效果，本文在现有模型基础上，考虑不同空间环境下行人的潜意识行为，为了更好的刻画行人疏散过程选择路径的偏向及决策，建立起具有潜意识效应的人群应急疏散格子气模型，数值上模拟了人群疏散的动力学因素。故此系统对人群疏散，踏踩事件有极好的模拟效果。

问题分析：

  因此对第二阶段: 针对问题一：本文继续研究人的行为模式对疏散结局的影响。此时, 疏散的必经之路是一条狭窄通道，通过研究物理环境变量结合人群疏散行为模型，构建疏散路线选择模型，以 Java 作为人群疏散仿真实验平台，对行人疏散过程中所表现出的有限理性路径决策机制进行仿真模拟，探究在狭窄通道内发生踩踏事件的风险，改变其主要物理变量探究其过程。
  针对问题 2: 客机在发生紧急情况时，机舱内的乘客需要进行快速撤离。客舱通道往往较为狭窄且不够通畅，而且此时由于乘客的慌乱，可能无法达成最理想的组织状态,这都给撤离行动的效率带来了挑战。
  本文通过研究不同应急疏散模型，并且对其建立角度，适用性以及模型具体算法等方面进行分析比较，提炼出相关结论，并且在传统社会力模型的基础上，模拟疏散行人转向和避让的预判行为，初步建立起飞机客舱的行为性修正社会力模型，并且与实验数据对比验证其有效性。

模型假设：

  1. 假设人群疏散变量中未有失能者。
  2. 假设模型建筑环境不存在固体破坏。

模型的建立与求解

  仿真时长取决于行人疏散所需要的时间，在仿真时用 cycle 来表示，疏散的时间就等于 cycle 数值和步长的乘积。仿真步长设为 1.0e-3，在人数较少和密度较小时只分析行人所受最大挤压力，在人数众多和密度较大的时候，在分析最大挤压力的同时，也对典型位置的人群受力进行分析。实验如下：
  实验一：在疏散人数为 30 人，密度为 1 4 2 / p m 的情况下，疏散过程中人群所受的最大挤压力如下图所示：

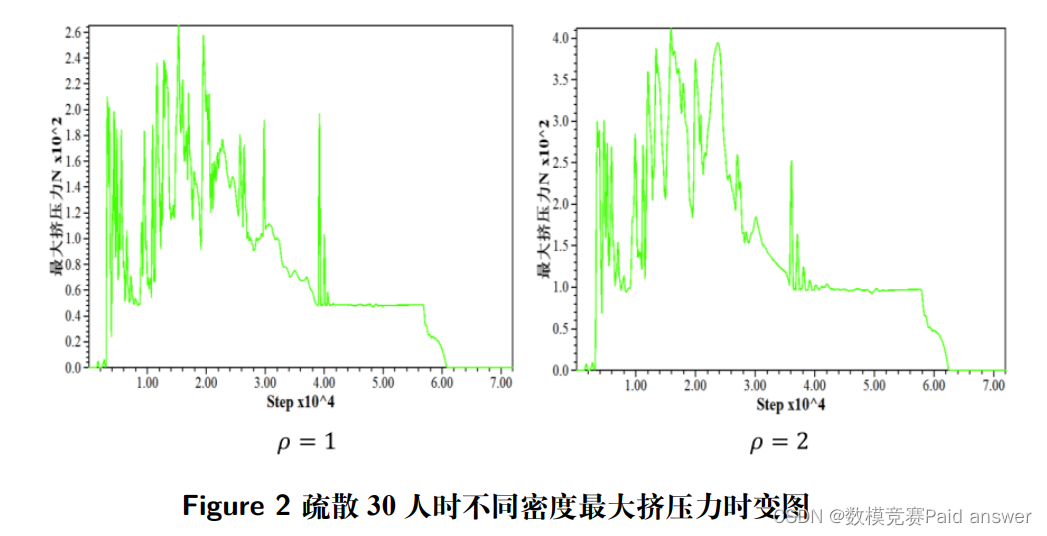
  实验二：在疏散人数为 96 人，密度为 1 6 2 / p m 时，疏散过程中人群所受最大挤压力如下图所示

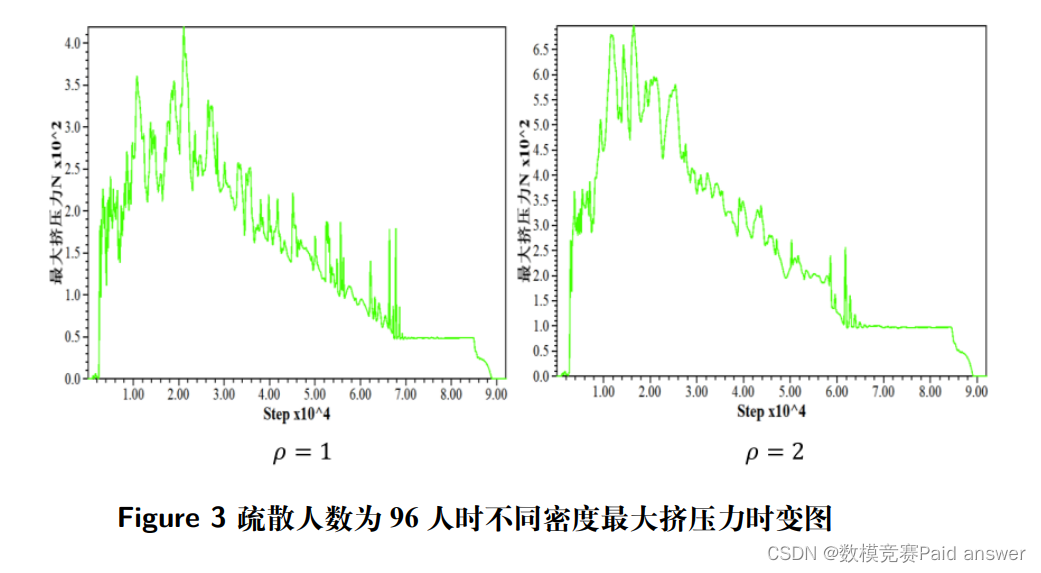
  实验结果分析：从曲线趋势来看：通过以上最大挤压力时变曲线图可以看出，在疏散过程中，人群内部最大挤压力随时间变化的趋势具有一致性，与人数、速度、密度大小无关。最大挤压力都呈现出短时间内升高，然后再慢慢降低。这是由于在疏散时，人会以较快的速度聚集在出口形成一个拱形，人群受力会突然变大，但由于人数众多，出口只有一个并且宽度有限，人群只能慢慢通过出口，受力会从峰值处慢慢降下来。从上图中可以看出，在最大挤压力慢慢减小的过程中，会出现极短时间内力突然升高的一个趋势，这是由于在疏散过程中，在前面粒子通过出口后，靠近出口两侧墙壁的粒子的运动趋势始终是朝向目标点，在经过出口的瞬间，会贴着墙壁最后出去，由于粒子和墙壁表面并不光滑，粒子会对墙壁产生一个较大的挤压力，导致受力突然升高，粒子通过后，最大挤压力就会降下来，直到慢慢减小为 0。

  利用整理的案例，明确造成事故发生的风险因子后，通过事故树来表示踩踏事件和风险因子的关系，通过定性分析，找出对事故发生影响最大的风险因子。
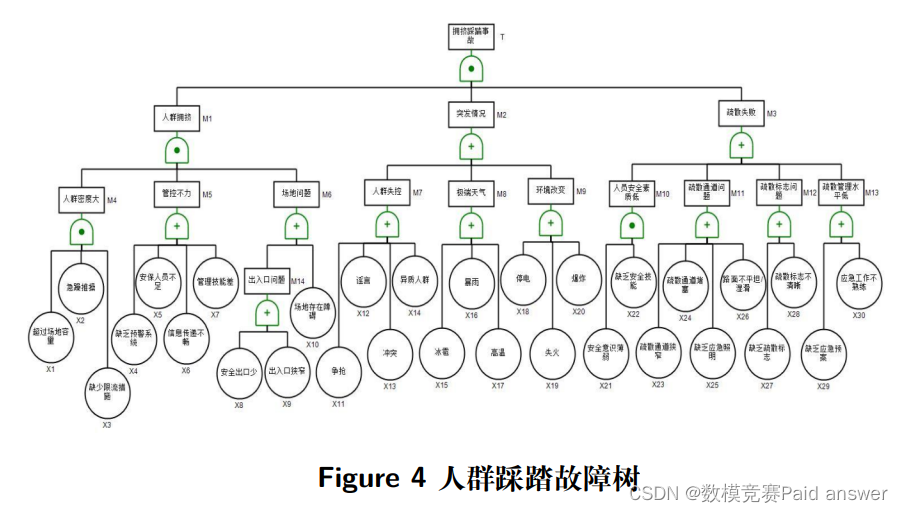
  不考虑特殊情况下，密集人群风险的顶上事件就是拥挤踩踏，因此以拥挤踩踏为顶上事件建立故障树。通过对拥挤踩踏实例的分析，按照踩踏事件发生的机制来制作故障树。
  由图 (4) 可知，踩踏是由人群拥挤，突发事件，疏散失败三个中间事件一块构成，逻辑上用与门连接。三个中间事件由 11 个次中间事件和 30 个基本事件构成，人群拥挤是由人群密度大、管控不力、场地问题通过与门构成。突发情况是由人群失控、极端天气、环境改变通过或门构成。疏散失败是由人员安全素质低、疏散通道问题、疏散标志问题、疏散管理水平低四个通过或门构成。编制的事故树和具体代号含义见下表：

基于 Agent 模型的踩踏风险评估模型

  Anylogic 是一个专业的虚拟原型环境，用于模拟设计具有离散、连续和混合行为以及高聚合性能的复杂系统。Anylogic 可以快速建立被设计系统和系统外围环境的仿真模型（即虚拟原型），包括物理设备、机械装置、混合系统等。同时，它是市场上为数不多的可以支持基于代理的智能建模和仿真的软件之一。同时，它也是市场上为数不多的可以支持基于代理的智能建模和仿真的软件程序之一。
  由此我们使用 Anylogic 建立出一个 60 × 60 的类矩形区域，分别将通道宽度调整为15、17、19 得出以下结论：


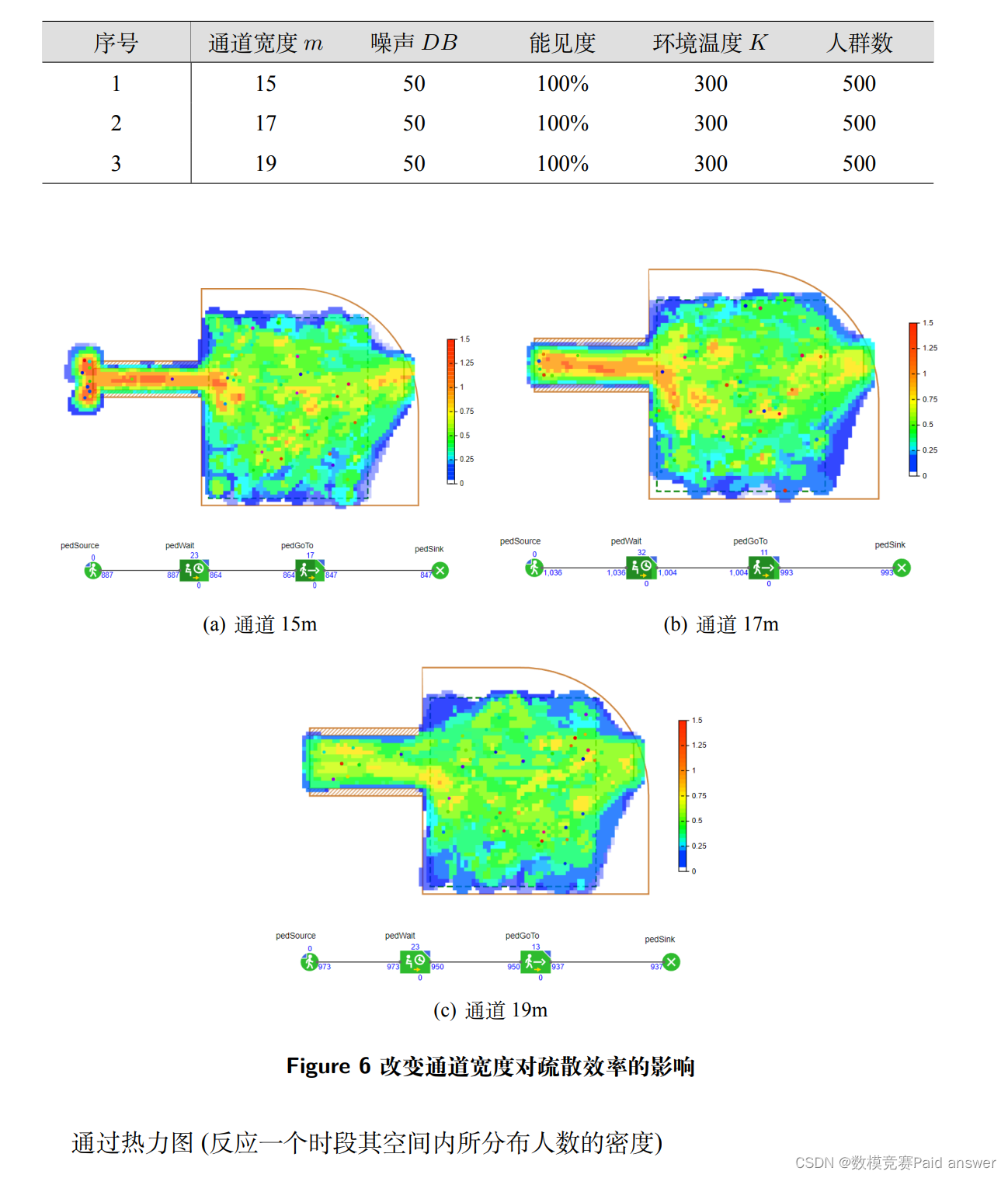
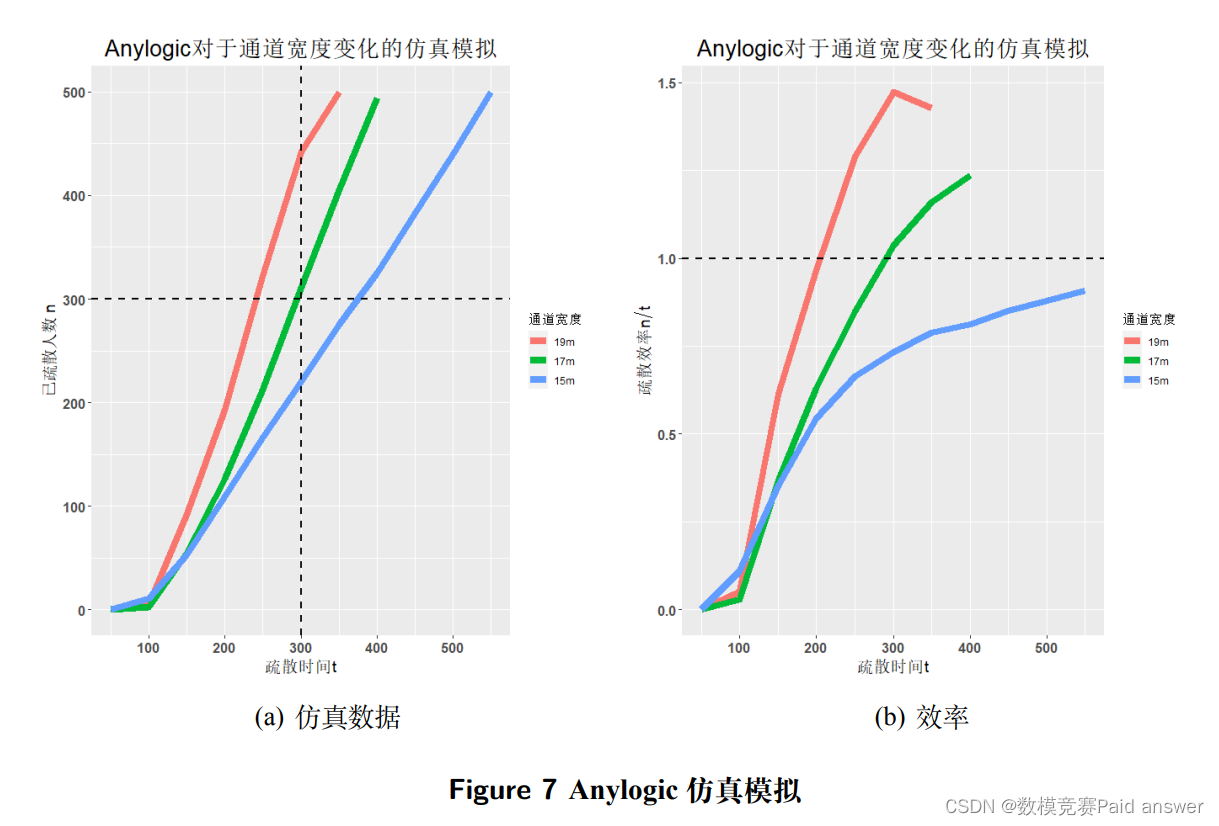
  明显可见, 通道宽度越宽疏散效率越高，踩踏风险越低，同时可以发现在其余变量不变时，通道宽度 17m 为疏散效率为 1 时的阈值，这可以说明在能够容纳 500 人的场所量级下，通道宽度的设置不得低于 17m。

加入 FDS 对能见度进行建模分析

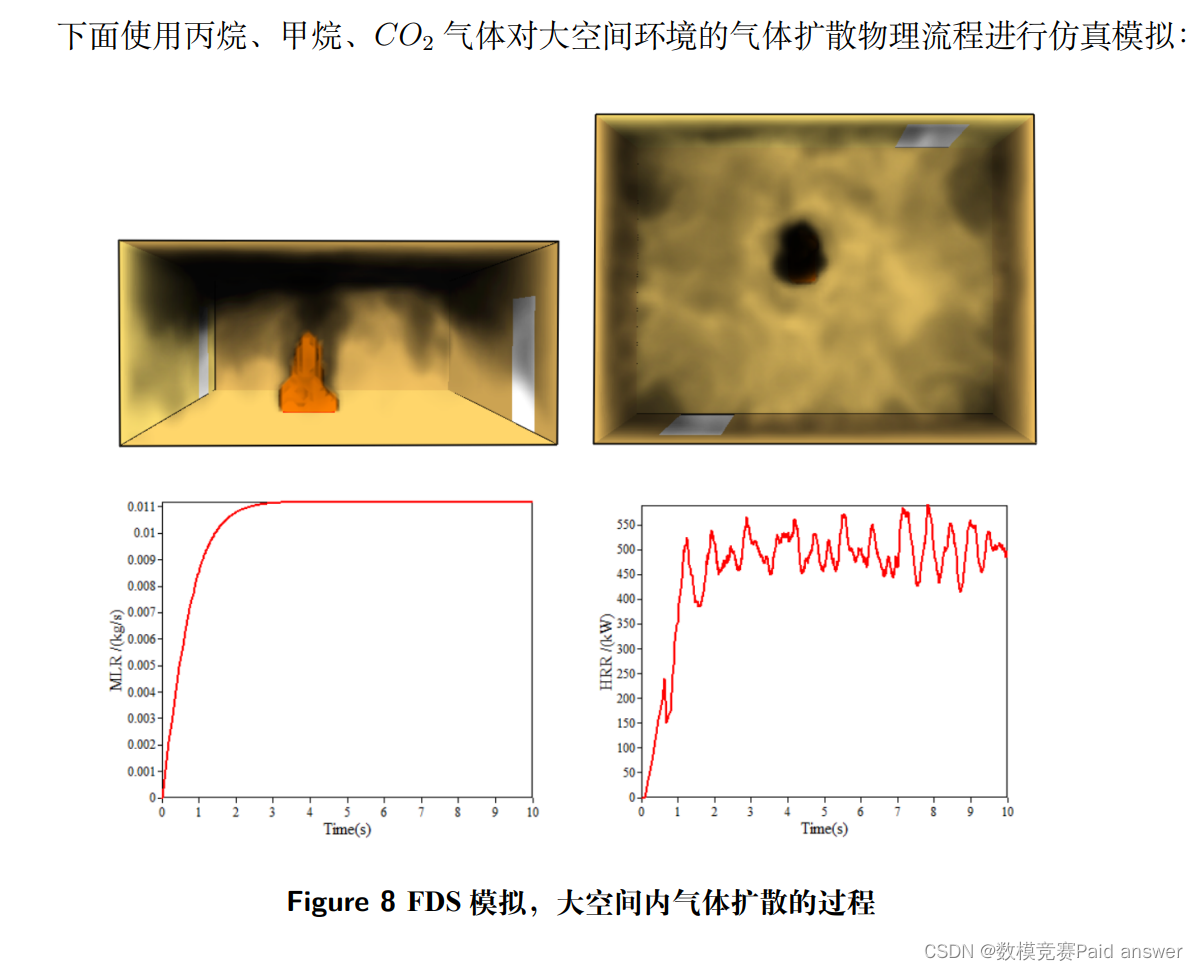
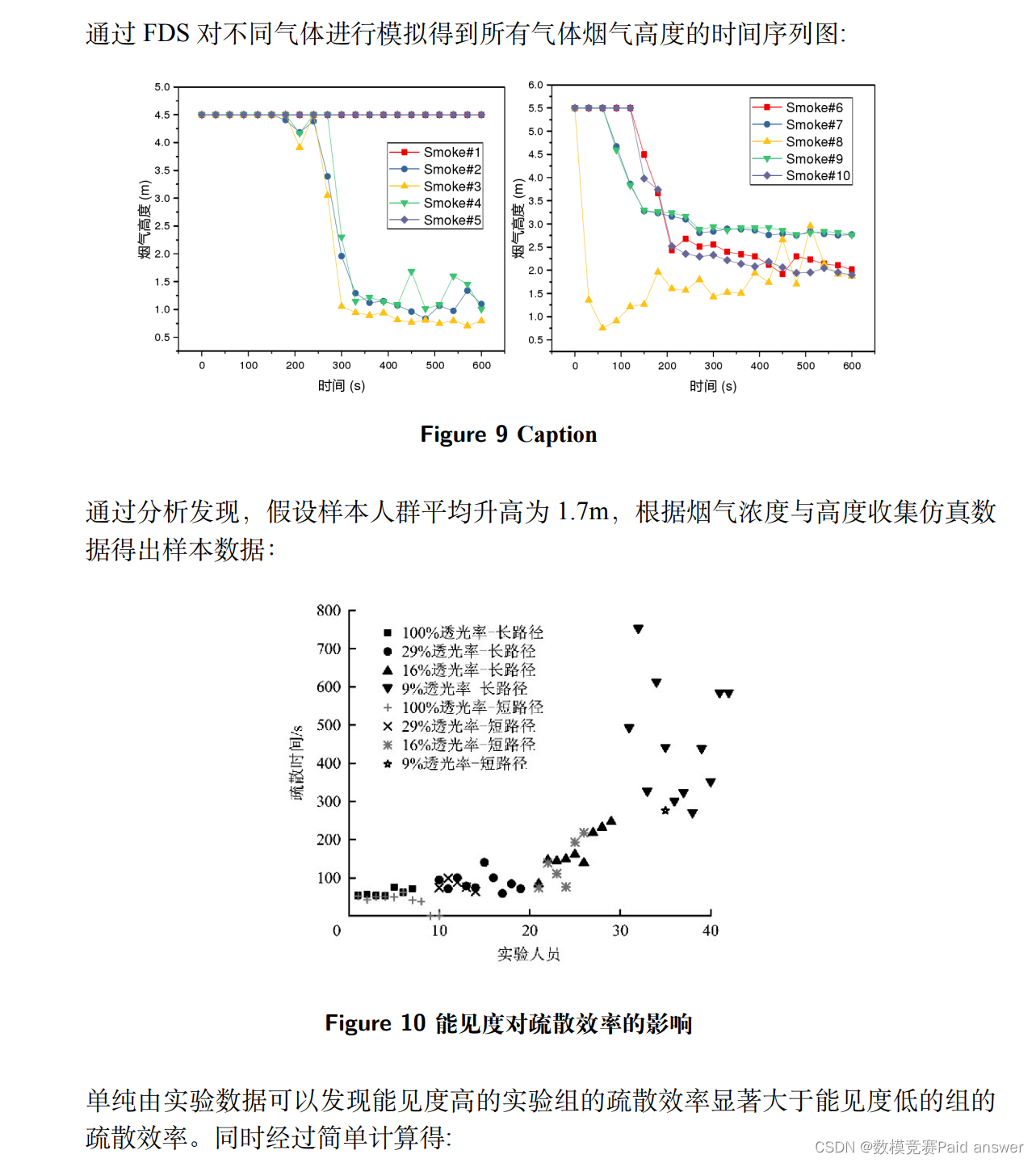
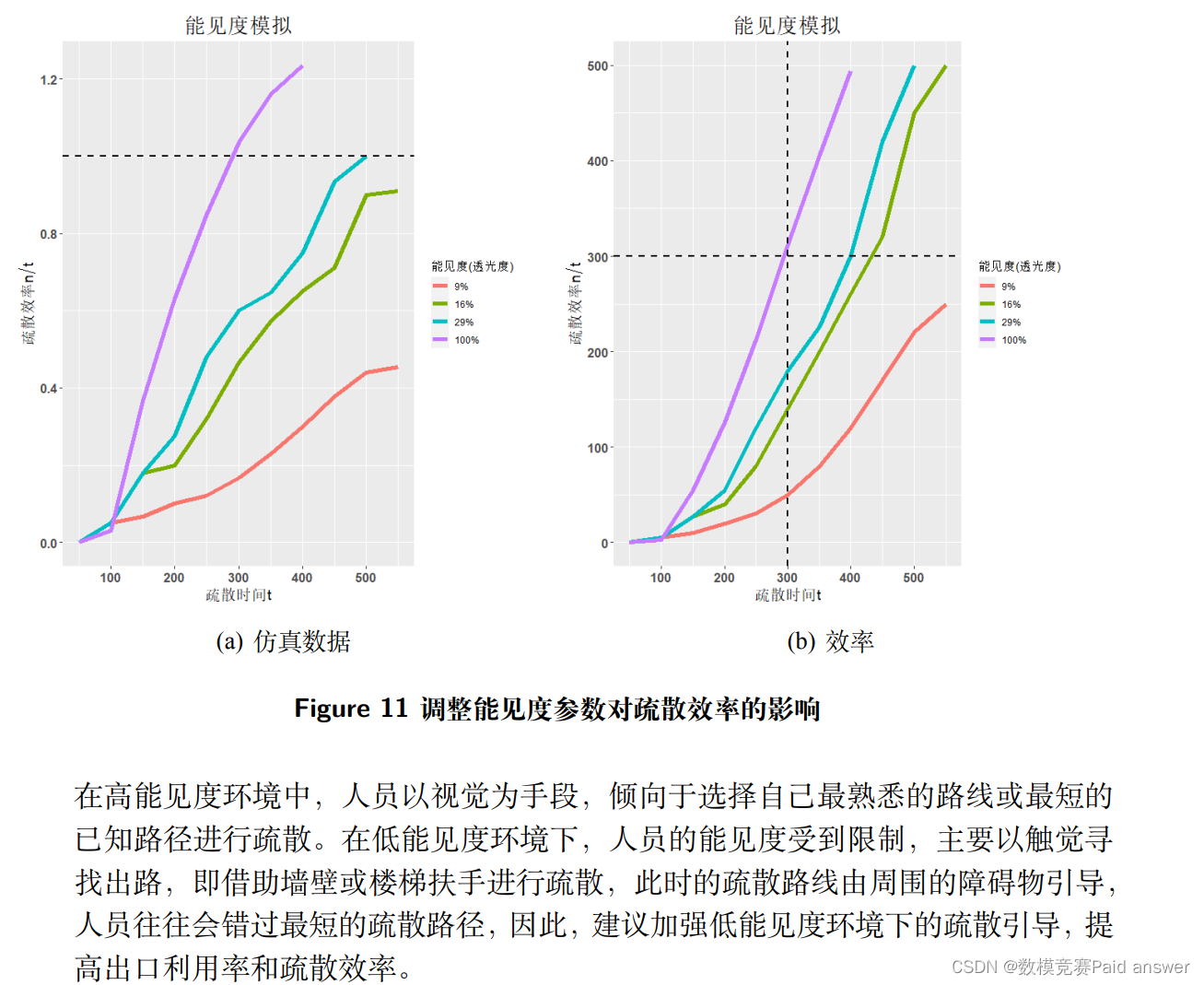
  客机在发生紧急情况时，机舱内的乘客需要进行快速撤离。客舱通道往往较为狭窄且不够通畅，而且此时由于乘客的慌乱，可能无法达成最理想的组织状态。这都给撤离行动的效率带来了挑战。
  本文通过研究不同应急疏散模型，并且对其建立角度，适用性以及模型具体算法等方面进行分析比较，提炼出相关结论，并且在传统社会力模型的基础上，模拟疏散行人转向和避让的预判行为，初步建立起飞机客舱的行为性修正社会力模型，并且与实验数据对比验证其有效性。

  修正社会力模型算法将转向因子与避让因子融合在预判规则中，并且结合实际受力情况、环境因素以及心理状态等因素相互作用，使得修正社会力模型成为实时动态的反馈模型，其算法流程图如图所示。

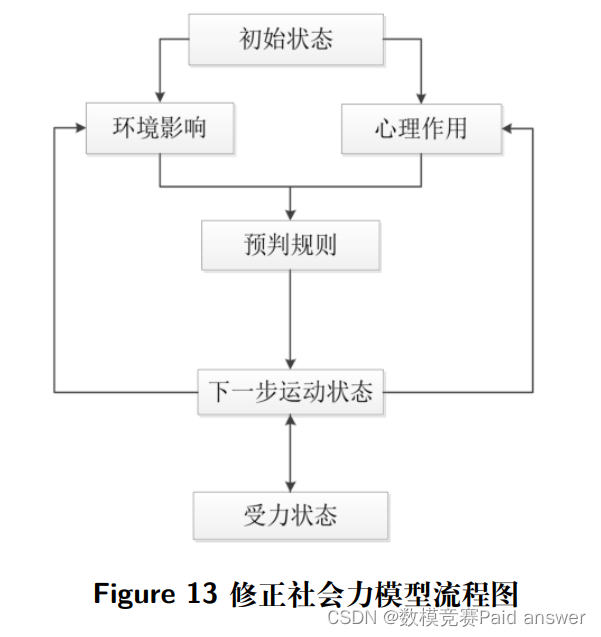
  修正社会力模型结构中每一步的前端都是疏散人员基于当前环境进行预判，预判规则基于原始社会力模型反馈引入转向因子和避让因子，从而疏散人员决定下一步运动状态。同时，随着疏散过程中周围环境变化和心理影响 (即认为是慌乱情绪为主导)，下一步运动状态也在实时改变，也影响疏散人员的受力状态。在受力状态发生改变时，也反向回馈到疏散人员的运动状态，修正社会力模型在连续实时的模型中寻求疏散人员的最佳疏散状态。

  为了验证改进后的社会力模型算法，模拟飞机客舱单通道疏散，两侧分别有 9 排座位，每侧每排随机安排三人，通过高空拍摄记录乘客疏散轨迹与疏散时间，如图 (14) 所示。在 AnyLogic 仿真平台搭建实验疏散场景如图 (15) 所示，, 连续仿真乘客在整个疏散过程中的疏散情况，同时对乘客疏散过程中进行预判距离，实时模拟乘客在疏散过程中遇到障碍物以及周围乘客的受力情况。同时，按照实验要求模拟竞争环境的疏散过程。

  模拟仿真蚁群算法, 在 MATLAB 中模拟蚁群算法，得出搜寻全局可以寻找到最大信息浓度的路径进而模拟疏散模型的求解能力，如图 (17) 可以看出蚁群算法在模型优化寻求最优解时有较好的的求解能力，仿真结果如下图所示



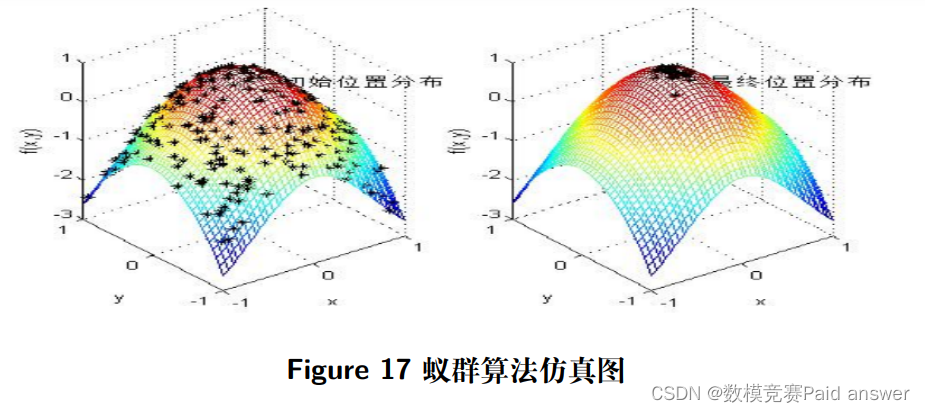
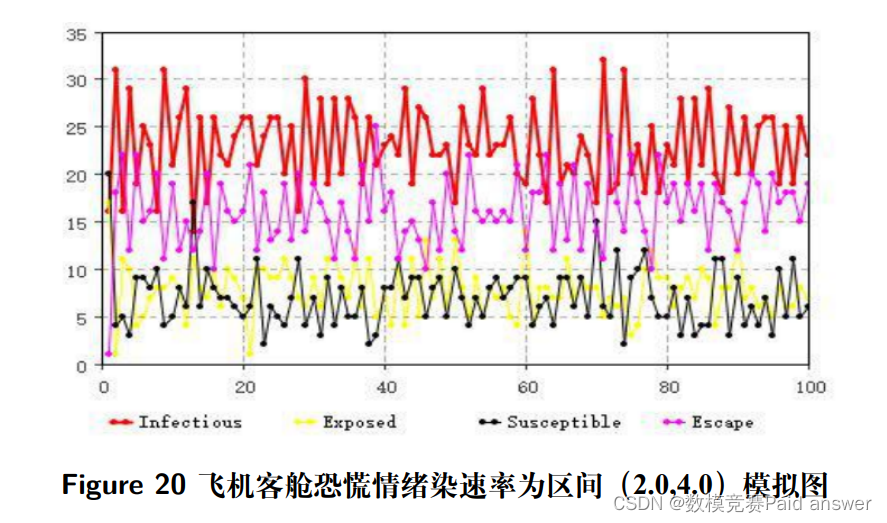
  此时, 引入风险避让力表达式, 即可以用蚁群算法得出修正社会力模型的最优解。但是基于疏散行人在疏散情况中的真实性, 疏散人群无法以最优解进行实际疏散, 因此, 需要在风险源排斥力加入系数 Q, 其中 Q 为最优解的正态分布系数, Q 需要结合飞机客舱具体疏散人员的身体状况、受教育程度以及心理承受力来具体标定, 综合状态评价最优的疏散行人即为正态分布的最大值, 而依照状态评估下降, Q 值会随机递减, 从而保证模型的适用真实性, 即飞机客舱基于情绪传导与信息反馈的修正社会力模型为:

关键因素对撤离效果的影响

  使用上述数学模型，本节探讨不同因素对疏散人员速率的影响，考虑两个因素：能见度和疏散门的宽度。2.3.1 客舱内的能见度已有的研究表明当能见度大于 30m 时，对人员疏散速度的影响可以忽略。所以此次对 30m 以内的不同能见度下疏散人员速度进行分别分析，如表 (22) 所示。当能见度在 10m 以上时，影响因子接近于 1；在 0.1 以下的影响因子为 0.2。

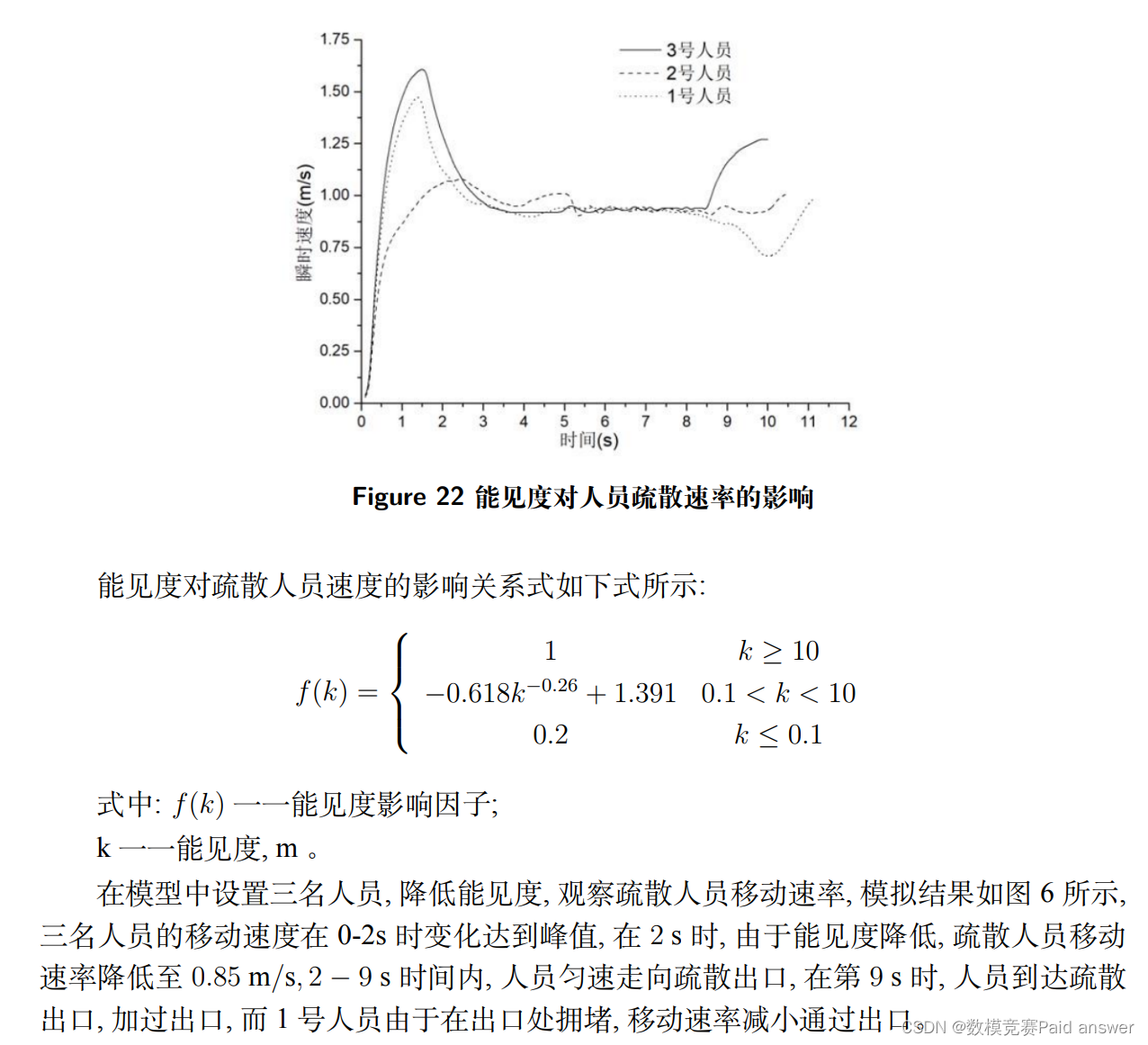
  Ma Peijie 和 Wang Binghong 用社会力模型研究了视野半径对客舱内的行人疏散的影响, 得出视野半径越小疏散时间越长 ; 当逃生人数超过标准阀值时, 其效果尤为显著。

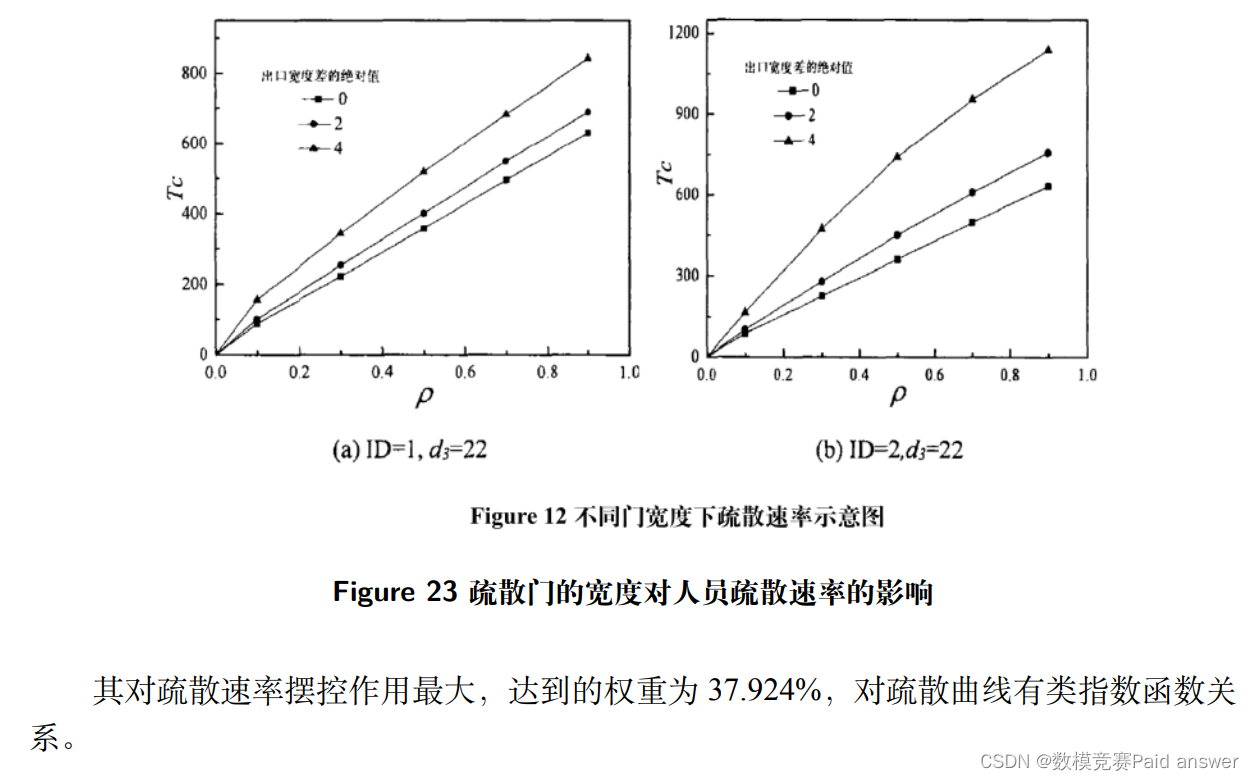
  使用 3–4–3 布局的双通道客机机舱大致结构如下:

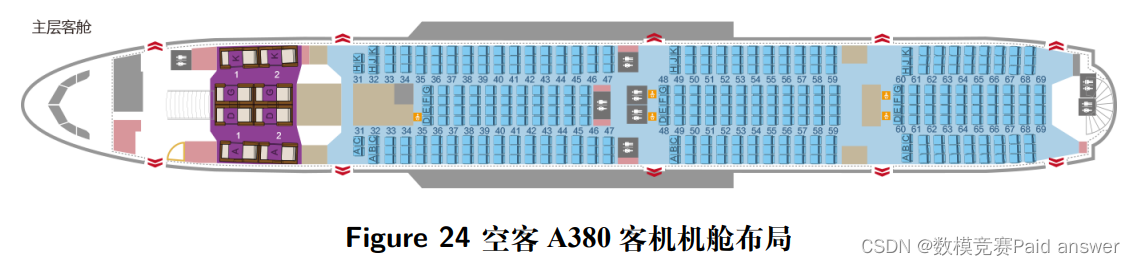
  本文对使用 3–4–3 布局的双通道客机机舱进行模拟计算, 仍然依用修改社会力模型进行模拟仿真:
  值得注意的是，本文使用修改社会力模型具有更好的仿真效果: 在仿真过程中截取同一时刻逃生者的仿真疏散对比图如下图所示，上图为传统社会力模型疏散图，下图为修正社会力模型疏散图。此外，同时疏散时间对比图为下图所示。

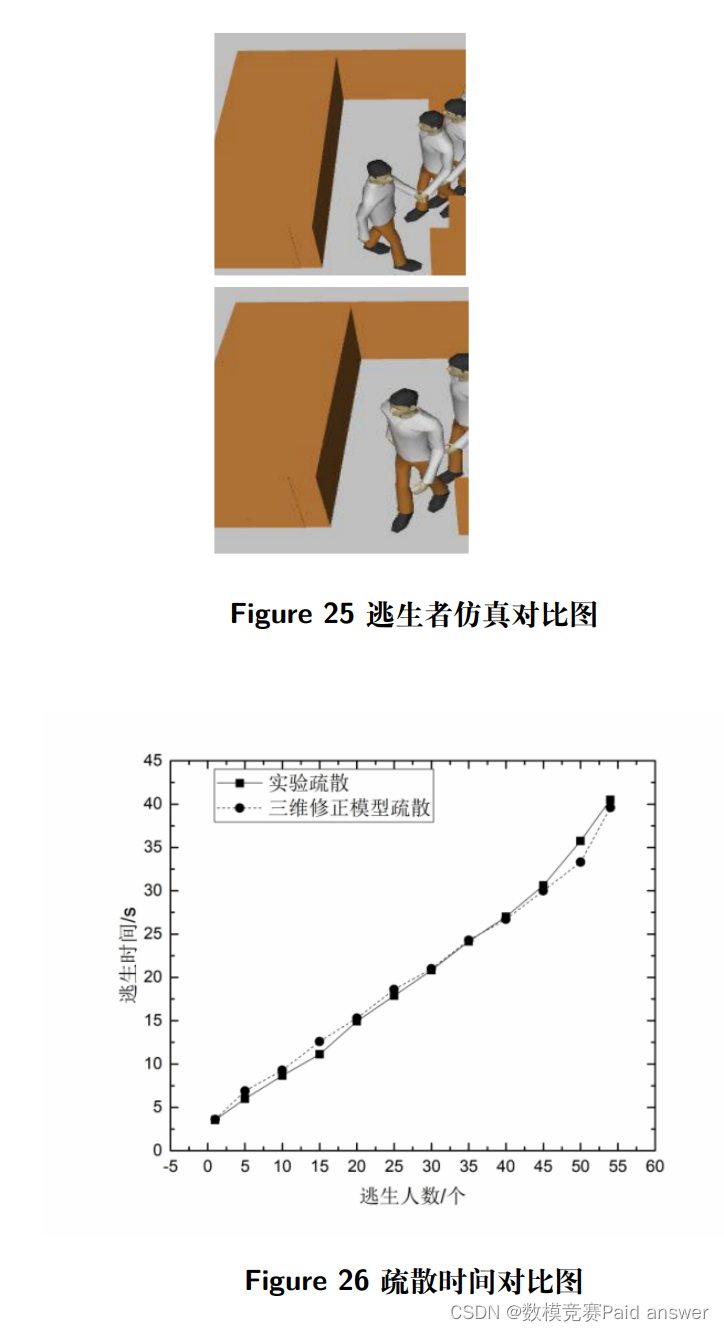
  在飞机客舱应急疏散实验中，分析疏散行人的运动状态和受力情况可以对整个疏散状态的瓶颈处以及疏散状态走向有较好的预测，而在真实实验中，疏散行人之间的物理力难以采集，心理力的计算则需要大量实验数据比较拟合后才能进行估算，因此，在飞机客舱应急疏散仿真实验中采用尽可能贴近真实行人的运动状态来反应疏散行人的受力状态，这里引用了修正社会力模型的疏散合力状态。
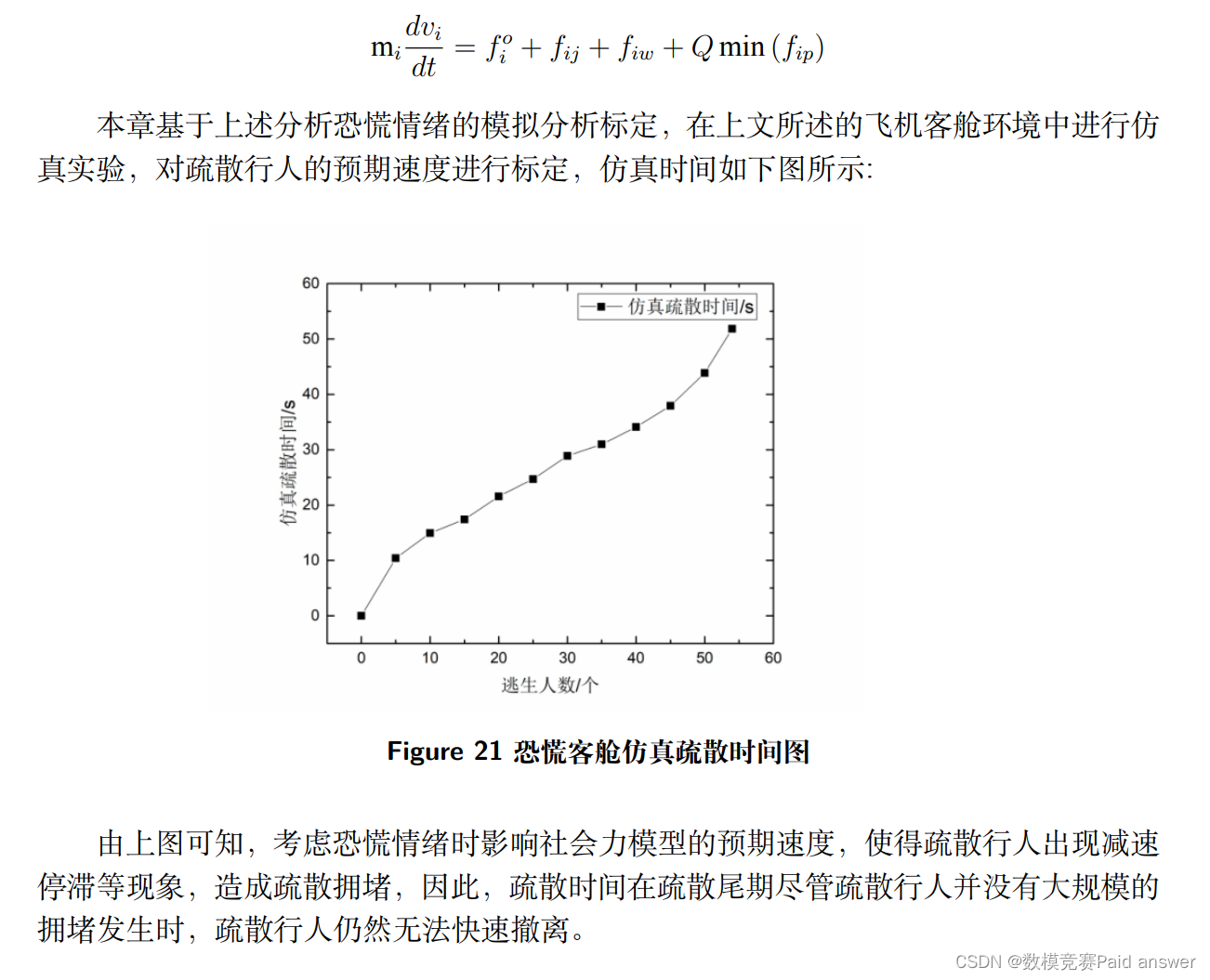
  基于飞机客舱应急疏散要求的特殊性，在模拟时选择开放一侧的舱门，应急疏散乘客基于客舱环境分为前门与后门两种，使用双通道逃生路径，经过多次仿真实验，逃生时间为 55s 左右，逃生时间如下图所示。

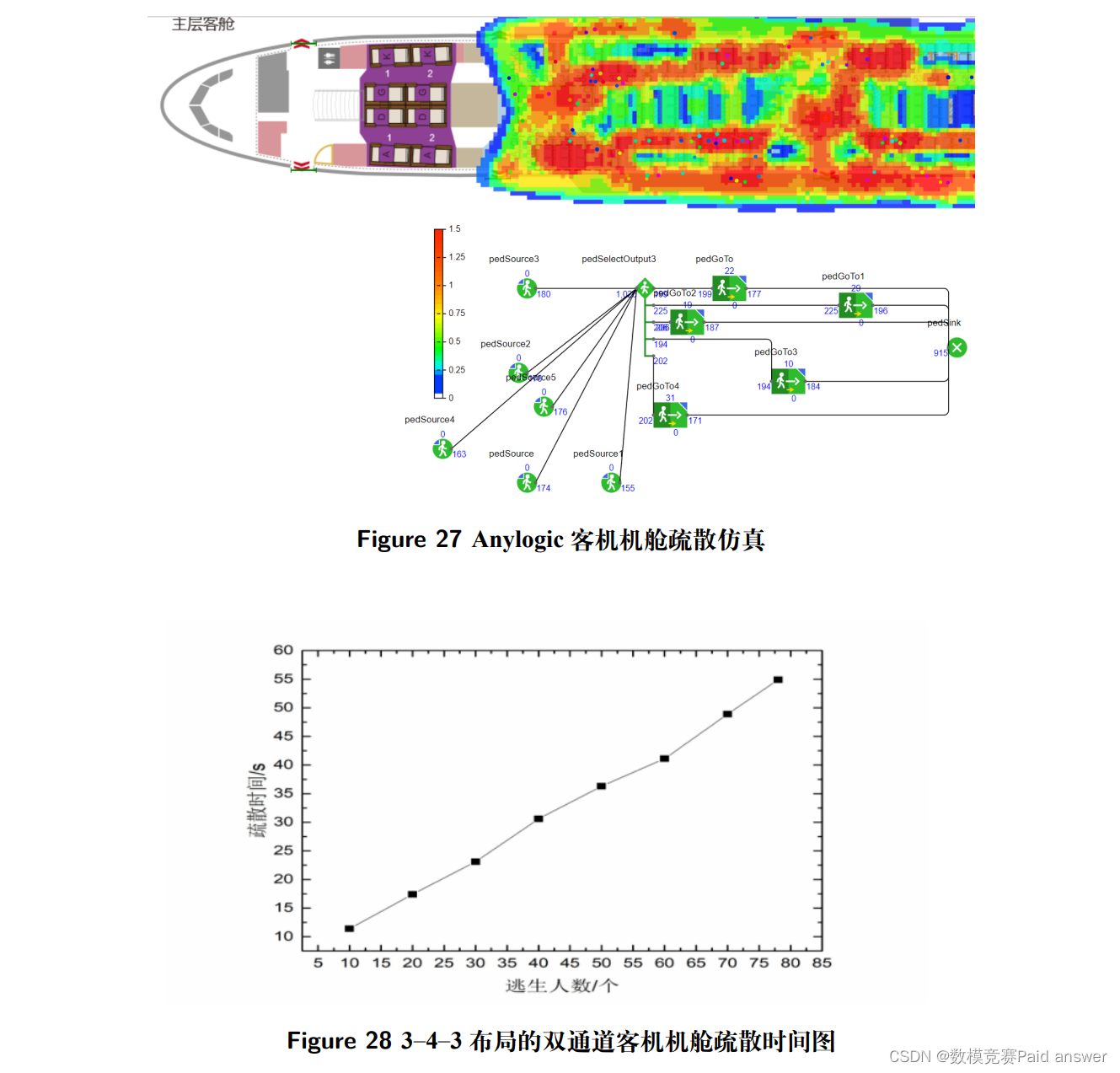
  在仿真前期，由于疏散个体经过距离的预判，疏散时间可能会高于实际的疏散时间，但在中后期仿真疏散时间会与真实疏散时间趋于吻合，因此，对于 3–4–3 布局机型的飞机客舱应急疏散时间有较好的预测性和可信度。

论文缩略图：

程序代码：

m=50:70;
t=0.5;
v_max=7;
v=0:1:7;
k=2.4*10^5;
k_1=1.2*10^5;
A_i=2*10^3;
B_i=0.08;
D_exit=0:1:10;
d=0:0.1:1;
z=0:0.1:1;
s=0:0.1:1;
h=0:0.1:1;
q=exp(1.5*(0.43*d+0.47*z+0.08*s+0.02*h))/exp(2);
hold on
for i=1:7
q=exp(14*(0.43*d+0.47+0.08+0.02))/exp(10);
f=1+q*10;
plot(d,f)
q=exp(14*(0.43+0.47*z+0.08+0.02))/exp(10);
f=i+q*10;
plot(z,f)
q=exp(14*(0.43+0.47+0.08*s+0.02))/exp(10);
f=i+q*10;
plot(s,f)
q=exp(14*(0.43+0.47+0.08+0.02*h))/exp(10);
f=i+q*10;
plot(h,f)
end
title('火灾人群疏散效率图')
xlabel('关键因素')
ylabel('疏散速率m/s')
legend('门宽','灾害严重程度','环境熟悉程度','肺活量')
axis([0 1,0 10])

clear;clc
%定义 用户界面
plotbutton=uicontrol('style','pushbutton',...
'string','Run',...
'fontsize',12,...
'position',[200,400,50,20],...
'callback','run=1;');
erasebutton=uicontrol('style','pushbutton',...
'string','Stop',...
'fontsize',12,...
'position',[300,400,50,20],...
'callback','freeze=1;');
number=uicontrol('style','text',...
'string','1',...
'fontsize',12,...
'position',[20,400,50,20]);
z=zeros(30,48);
cells=z;%元胞矩阵
weith=30;length=48;
x0=1;y0=12;%最佳出逃位置
peoplemidu=0.4;%人员密度
%危险度
for i=1:weith;
for j=1:length;
if(j>10 && j<13 && i>1)
pd(i,j)=j-1;
end
if(j>10 && j<13 && i==1)
pd(i,j)=0;
else
pd(i,j)=sqrt((i-x0)^2+(j-y0)^2);
end
end
end
%%%%初始化选择矩阵
for i=1:weith;
for j=1:length;
choice{i,j}=[0 0];
end
end
%%%%初始化人群
for i=1:weith
for j=1:length
if(rand<=peoplemidu)
cells(i,j)=1;
pv(i,j)=1;
choice{i,j}=[i j];
end
end
end
imh = imshow(cat(3,cells,cells,cells));
axis equal
axis tight
stop= 0;
run = 0;
freeze = 0;
%%%%开始逃生
while (stop==0)
if(run==1)
for i=1:weith
for j=1:length
if(cells(i,j)~=0)
if (j>=10&&j<13&&i==1)
choice{i,j}=[0 0];
cells(i,j)=0;
else
[newi,newj]=findnew(i,j,pd); %找到选择位置
if(pd(i,j)>pd(newi,newj))
if(same(newi,newj,choice)~=0)
choice{i,j}=[newi newj];
else
choice{i,j}=[i j];
end
end
if (pd(i,j)==pd(newi,newj))
if(same(newi,newj,choice)~=0)
if(rand>=0.5)
choice{i,j}=[newi newj];
else
choice{i,j}=[i j];
end
else
choice{i,j}=[i j];
end
end
if (pd(i,j)<pd(newi,newj))
if(same(newi,newj,choice)~=0)
if(rand>0.2)
choice{i,j}=[i j];
else
choice{i,j}=[newi newj];
end
else
choice{i,j}=[i j];
end
end
end
end
end
end
for i=1:weith
for j=1:length
if(choice{i,j} ~= [0 0])
m=choice{i,j};
ii=m(1);jj=m(2);
cells(ii,jj)=1;
cells(i,j)=0;
end
end
end
for i=1:weith
for j=1:length
if(cells(i,j)~=0)
choice{i,j}=[1 1];
else
choice{i,j}=[0 0];
end
end
end
pause(0.1);
set(imh, 'cdata', cat(3,cells,cells,cells) )
stepnumber = 1 + str2num(get(number,'string'));
set(number,'string',num2str(stepnumber))
end
if (freeze==1)
run = 0;
freeze = 0;
end
drawnow
end
%%%% 判断是否已经选择重复
function rt=same(newi,newj,choice)
rt=1;
for i=1:30
for j=1:48
if([newi newj]==choice{i,j})
rt=0;
break;
end
end
end
%%%%%%% 寻找新位置
function [newi,newj]=findnew(i,j,pd)
if(j>=1 && j<42 && (i==1 || i==30))
newi=i;newj=j+1;
end
if(j>=13 && (i==1 || i==30) )
newi=i;newj=j-1;
end
if(i>=2 && i<=29 && j==1)
newi=i;newj=j+1;
end
if(i>=2 && i<=29 && j==48)
newi=i;newj=j-1;
end
if(i==30&&j>=10&&j<45)
newi=i-1;newj=j;
end
if(i>=2&&i<=29&&j>=2&&j<=47)
a=[pd(i-1,j-1) pd(i-1,j) pd(i-1,j+1) pd(i,j-1) pd(i,j+1) pd(i+1,j-1) pd(i+1,j)
pd(i+1,j+1)];
[m,n]=min(a);
switch n
case 1
newi=i-1;newj=j-1;
case 2
newi=i-1;newj=j;
case 3
newi=i-1;newj=j+1;
case 4
newi=i;newj=j-1;
case 5
newi=i;newj=j+1;
case 6
newi=i+1;newj=j-1;
case 7
newi=i+1;newj=j;
otherwise
newi=i+1;newj=j+1;
end
end

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可