给我们一个二叉树,我们应该如何来求二叉树的最小深度呢?
二叉树的最小深度指的是叶子结点到所处的位置最小的,这就是二叉树的最小深度,也就是说我们要找的是离根结点最近的叶子结点。如果我们从根结点向下出发寻找叶子节点,一层一层的去找叶子结点最先找到的叶子结点所处于的深度就是二叉树的最小深度,而叶子结点的标志就是两个指针域都为NULL。所以我们只需要去寻找最先出现的二叉树的两个指针域都为NULL的结点。
但是从上往下去寻找的话,分叉是很多的,这不方便我们的查找,因为分叉越多的话,你先选择遍历哪一条分叉呢?你怎么知道所选的这一条分叉上的叶子结点离根结点最近呢?如果你所选的这一条分叉上找的叶子结点不是离根结点最近的,那么你该怎么选择下一个路径呢?这些都是我们要考虑的问题,就算我们按照从左到右的顺序依次遍历每一条路径去计算路径的长度,我们是不是需要建立一个数组来储存每一个叶子结点到根结点的路径长度,然后再从中挑选最小的。这是很麻烦的。
但是我们换一个思路,从下往上去计算叶子结点到根结点的路径长度,因为按照递归,递归终止条件一旦达成,函数就会逐层返回,在二叉树上的表现就是从叶子结点逐层向上。按照下面图示的方法去计算最小深度你看看是不是更为简单,叶子结点的深度为1(可以看左只有根结点的一颗子树):
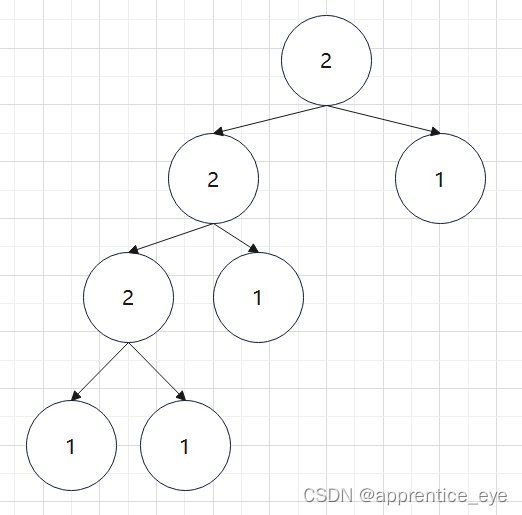
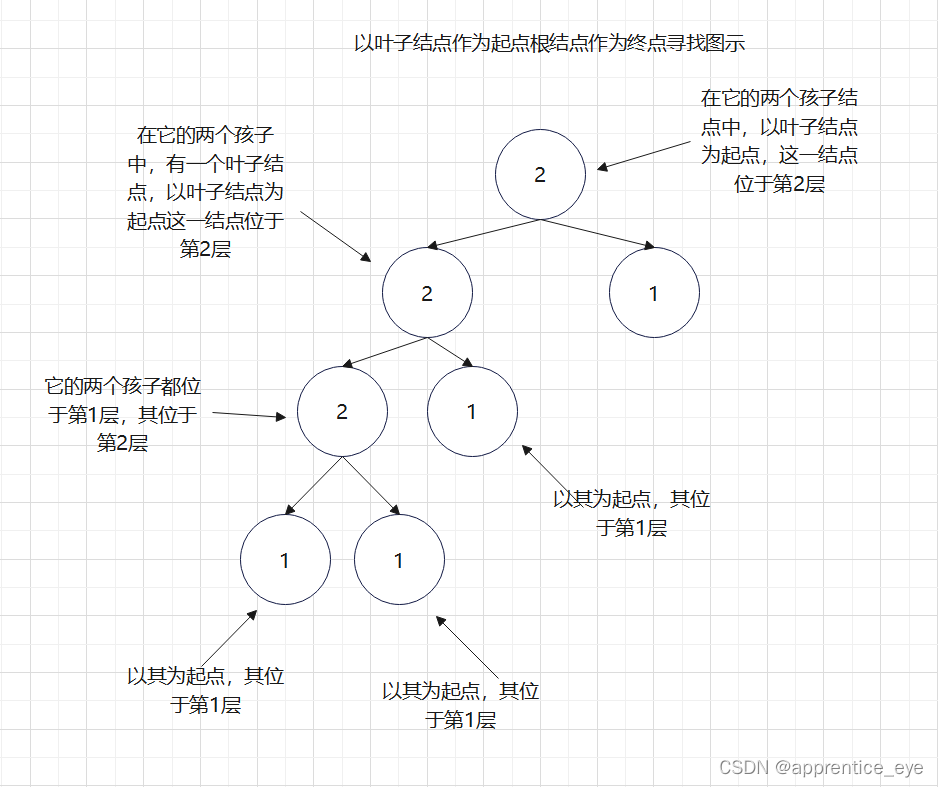
相信你看了图示之后,大概就明白了,这就是一个不断地从结点的两个子树中以较矮的子树作为长度,然后不断向上知道到达根结点的过程,这一过程可以在递归中自动实现。接下来我们来分析递归的终止条件,一旦访问到
r
o
o
t
=
=
N
U
L
L
root==NULL
root==NULL说明这一个结点不存在可以看作根结点为空的子树,深度看作0,返回0即可,如果访问的当前结点的左孩子为NULL右孩子也为NULL,说明此节点为叶子结点,按照上图分析,叶子结点是起点返回1,当访问到空结点时此节点不存在,但是如果其兄弟结点存在的话就必定只能从其兄弟所在的路径继续向上,也就是以不为0的路径加1作为当前结点所在路径的最短长度。这样我们就分析路径的变化规则,我们可以写出下面的代码:
int minDepth(struct TreeNode* root) {
if(root==NULL)return 0;
if(root->left==NULL&&root->right==NULL)
return 1;
int left = minDepth(root->left);
int right = minDepth(root->right);
int depth;
if(left!=0&&right!=0){
depth = left>right?right+1:left+1;
}
if(left==0){
depth = right+1;
}
if(right == 0){
depth = left +1;
}
return depth;
}
运行结果截图:


![【算法每日一练]-单调队列,滑动窗口(保姆级教程 篇1) #滑动窗口 #求m区间的最小值 #理想的正方形 #切蛋糕](https://img-blog.csdnimg.cn/fb8a0cd6585a41738fa99b61c1a8d7eb.png)


![[vuex] unknown mutation type: SET_SOURCE](https://img-blog.csdnimg.cn/f25632fba81b4a0992b467ce7e48377b.png)





![路径总和[简单]](https://img-blog.csdnimg.cn/60348911162c46298b7362e67cee9db9.png)
