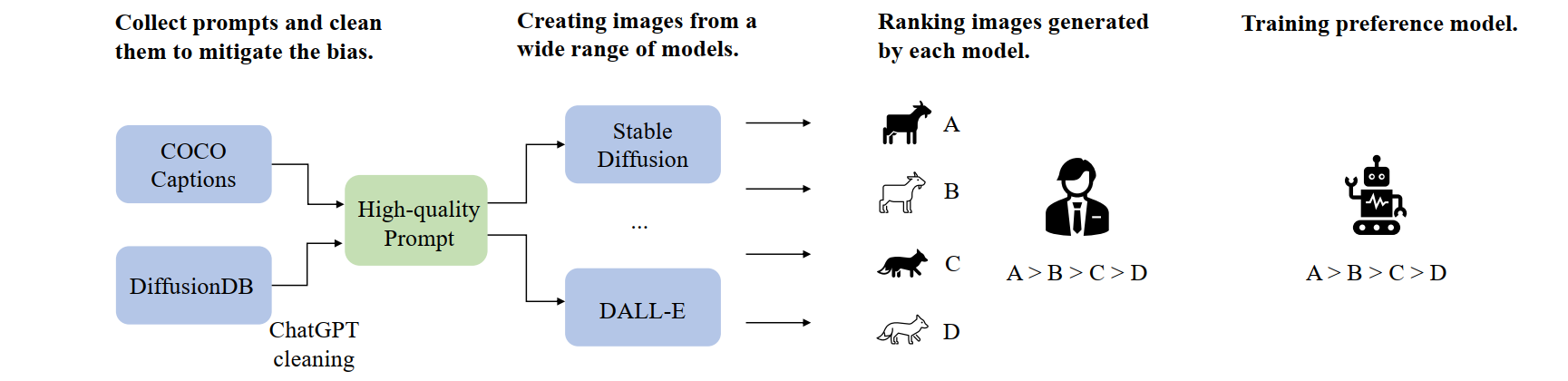
今天讲单调队列
目录
题目:滑动窗口
思路:
题目:求m区间的最小值
思路:
题目:理想的正方形
思路:
题目:切蛋糕
思路:
一共两种类型:一种是区间中的最值(滑动窗口),另一种是区间和的最值(切蛋糕),原理一样。
题目:滑动窗口
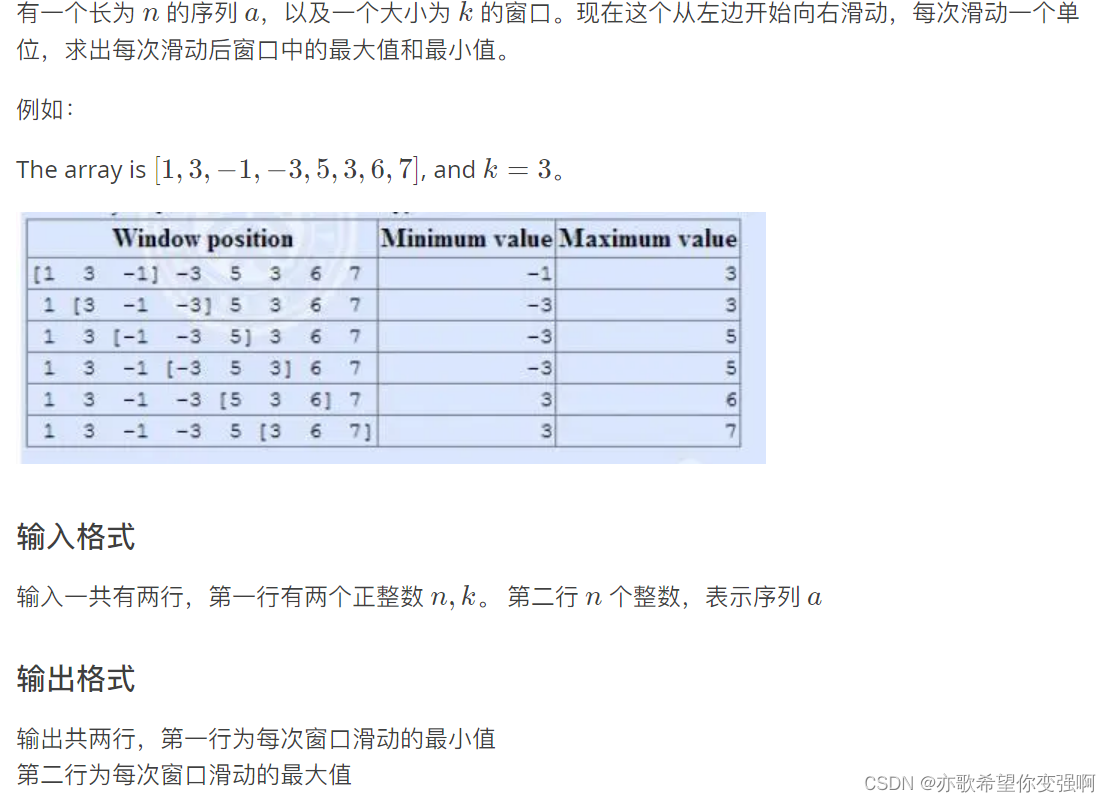
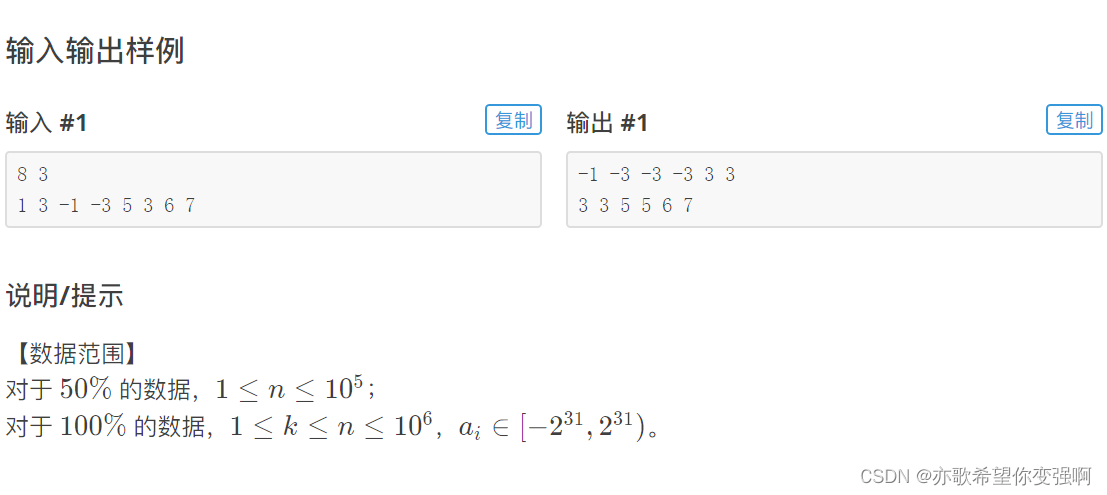
思路:
放这个题是为了给出模板。
单调队列使用注意事项:(遍历i就要维护[i-k+1,i]的单调区间,从而遍历所有的i)
入队新元素为i 过期队头和i-k+1比较即q[h]<i-k+1
队尾出队是a[i]<a[q[t]](取不取等都一样,因为新元素来了都要入队)队头过期是q[h]+k<i+1
1,维持单调:剔除因新来的元素导致的不单调元素
2,队尾入队:新来元素一定入队(以便更新队尾下标,方便和下一个新元素比较)
3,过期出队:队头元素的下标是否越界(和队头指针值无关)
#include <bits/stdc++.h>
using namespace std;
int n,k;
int q1[1000001],q2[1000001],a[1000001];
void min_deque()
{
int h=1,t=0;//h是头,t是尾(h和t的值没有任何意义,就当成front和back)
for(int i=1;i<=n;i++)//从第一个数开始滑动
{ //开始对上个元素的队列进行更新
while(h<=t&&a[i]<a[q1[t]]) t--;//(维持单调)新元素入队后,剔除无效元素
q1[++t]=i; //新元素入队操作
if(q1[h]+k<=i) h++;//过期决策从队头出队
if(i>=k) printf("%d ",a[q1[h]]);//输出最值
}
cout<<endl;
}
void max_deque()
{
int h=1,t=0;
for(int i=1;i<=n;i++)
{
while(h<=t&&a[i]>a[q2[t]]) t--;
q2[++t]=i;
if(q2[h]+k<=i) h++;
if(i>=k) printf("%d ",a[q2[h]]);
}
}
int main()
{
cin>>n>>k; //n为长度,k为窗口大小
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
min_deque();//维护两个单调队列
max_deque();
return 0;
}
题目:求m区间的最小值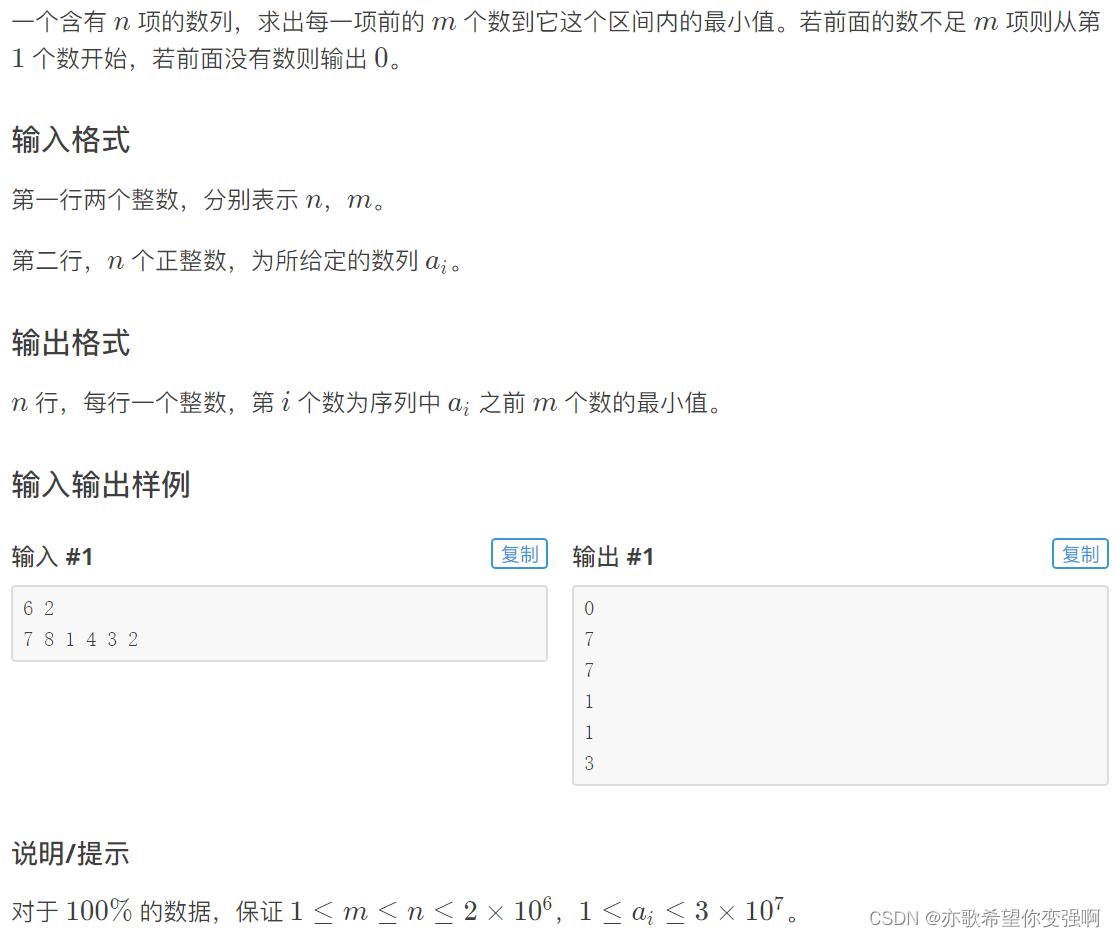
思路:
就是遍历i时候,要创建维护[i-m,i-1]的最小值的单调队列,从而遍历所有的i
入队新元素为i-1 所以h<=t&&a[q[t]]>a[i-1]
过期队头和i-m比较 h<=t&&q[h]+m<i
#include <bits/stdc++.h>
using namespace std;
const int N=2e6+5;
int n,m,a[N],q[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
int h=1,t=0;
cout<<0<<'\n';
for(int i=2;i<=n;i++){
while(h<=t&&a[q[t]]>a[i-1])t--;
q[++t]=i-1;
while(h<=t&&q[h]+m<i)h++;
cout<<a[q[h]]<<'\n';
}
return 0;
}
题目:理想的正方形
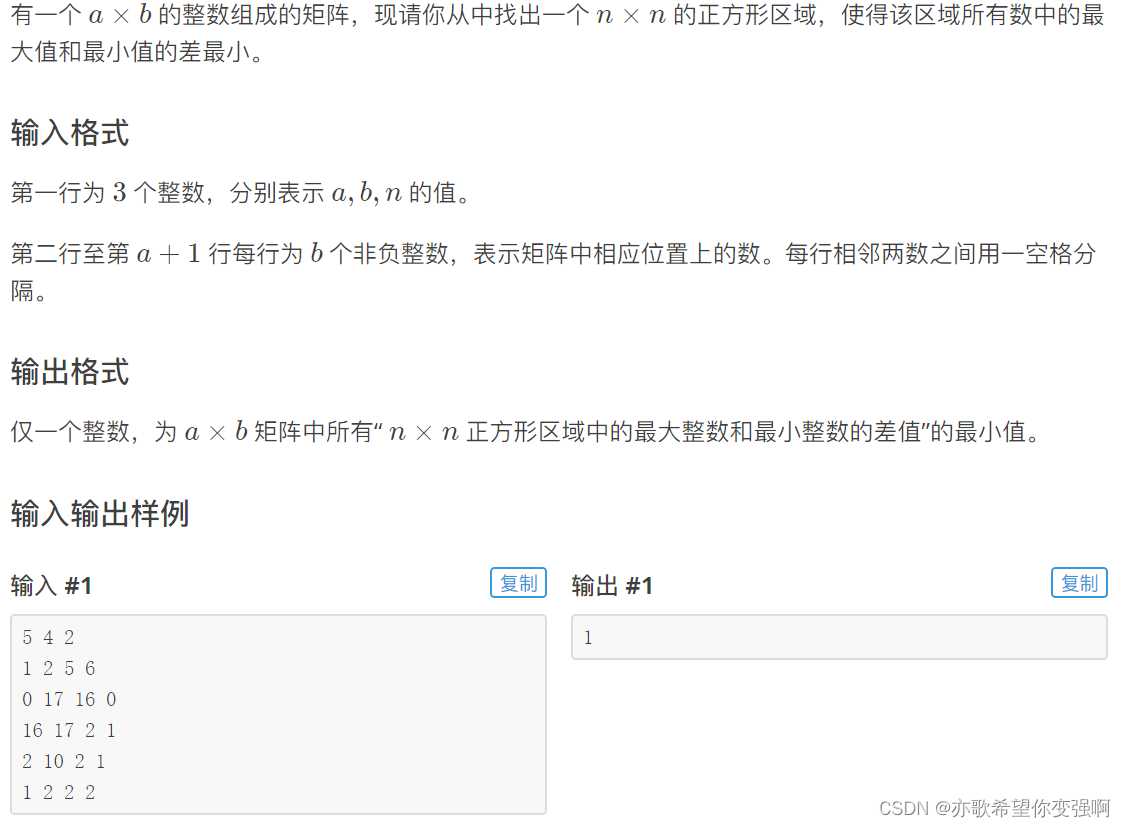
思路:
之前讲的是一维的区间最值,现在的是二维区间最值,那么维护二维的单调队列即可。
操作:
先对原矩阵进行列压缩,使用单调队列一行一行处理,然后再对压缩后的矩阵进行行压缩,一列一列处理
注意事项:
1,处理完后要从头开始放元素,这时就要注意别让下标越界了!!!
2,注意每个矩阵的行列数,可不一样,别写错了!!!
2,这个写法只针对小矩阵边长不为1 ,当为1时就需要特判处理,在外层循环加上:(memcpy(min2,min1,sizeof(min2));break;)
#include <bits/stdc++.h>//P2216:
using namespace std;
int n,m,k,h,H,t,T,ans;
int a[1001][1001],q[1001],Q[1001];//设置两个队列,以便同时完成最大值和最小值,
int x[1001][1001],X[1001][1001];//X,x为第一次压缩后的矩阵
int y[1001][1001],Y[1001][1001];//Y,y为最终最大值和最小值矩阵
void two_deque(){
for (int i=1;i<=n;i++)//按行来处理(列压缩)同时处理最大值和最小值,不然一共要处理4次
{
H=T=h=t=Q[1]=q[1]=1; //同时完成最大值矩阵和最小值矩阵的行压缩
for (int j=2;j<=m;j++)
{
while (a[i][j]>=a[i][Q[T]]&&H<=T) T--;//维持单调性(剔除元素,可以不加等号)
while (a[i][j]<=a[i][q[t]]&&h<=t) t--;
Q[++T]=j;q[++t]=j;//新元素一定入队
while (j-Q[H]>=k) H++;//过期出队
while (j-q[h]>=k) h++;
if (j>=k) X[i][j-k+1]=a[i][Q[H]],x[i][j-k+1]=a[i][q[h]];
}
}
for (int j=1;j<=m-k+1;j++)//按列来(注意列变少了)
{
H=T=h=t=Q[1]=q[1]=1; //同时完成最大值矩阵和最小值矩阵的列压缩
for (int i=2;i<=n;i++)
{
while (X[i][j]>=X[Q[T]][j]&&H<=T) T--;
while (x[i][j]<=x[q[t]][j]&&h<=t) t--;
Q[++T]=i;q[++t]=i;
while (i-Q[H]>=k) H++;
while (i-q[h]>=k) h++;
if (i>=k) Y[i-k+1][j]=X[Q[H]][j],y[i-k+1][j]=x[q[h]][j];
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);//n,m为矩阵大小,k为需要输出的正方形大小(输出所有方形中极差的最小值)
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
two_deque();
ans=0x3f3f3f3f;
for (int i=1;i<=n-k+1;i++)
for (int j=1;j<=m-k+1;j++)
ans=min(ans,Y[i][j]-y[i][j]);
printf("%d\n",ans);
return 0;
}
题目:切蛋糕

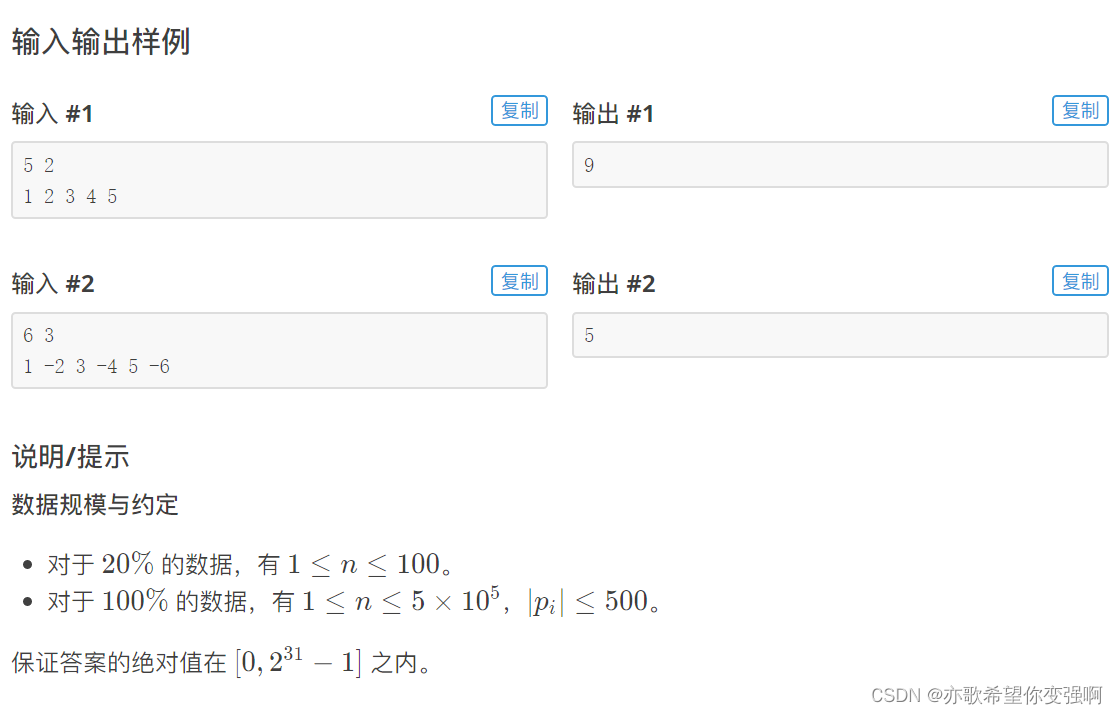
思路:
首先我们这道题是要不定长的前缀和,最优前缀和是max{sum[i]−sum[j],0}(i-j<=m),我们按题意固定i后就是max(0,sum[i]−min{sum[j]})。
也就是我们只需要维护[i-m+1,i]中最小的sum[j]即可,但是窗口右固定大小,所以要剔除过期的决策
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,INF=1e9;
int sum[N],q[N],ans=-INF;//注意有可能有负数
int main()
{
int n,m;scanf("%d%d",&n,&m); //n为蛋糕块数,m为窗口大小
for (register int i=1;i<=n;++i)
{
int x;scanf("%d",&x);
sum[i]=sum[i-1]+x;//求前缀和
}
int head=1,tail=1;q[1]=0;
for (register int i=1;i<=n;++i)
{ //对上个元素的队列处理
while (head<=tail&&q[head]+m<i+1) head++;//过期的最优决策出队 ,这里不能取等哦
while (head<=tail&&sum[i]<=sum[q[tail]]) tail--;//(维持单调)新元素i入队会使一些元素“无效 ”
q[++tail]=i;
ans=max(ans,sum[i]-sum[q[head]]);
}
printf("%d\n",ans);
return 0;
}
也可这样
// 也可以这么写,(<queue>头文件)
//访问:front,back 操作:pop_front,pop_back,push_front;push_back
deque<int>q; //deque是双向队列
q.push_back(0);
for(int i=1;i<=n;i++)
{
while(!q.empty()&&q.front()+m<i) q.pop_front();//越界就pop
ans=max(ans,sum[i]-sum[q.front()]);
while(!q.empty()&&sum[q.back()]>=sum[i]) q.pop_back();//递减就pop
q.push_back(i);
}

![[vuex] unknown mutation type: SET_SOURCE](https://img-blog.csdnimg.cn/f25632fba81b4a0992b467ce7e48377b.png)





![路径总和[简单]](https://img-blog.csdnimg.cn/60348911162c46298b7362e67cee9db9.png)