pytorch基础语法问题

shape

import torch
# 创建一个形状为(2, 3)的张量
x = torch.Tensor([[1, 2, 3], [4, 5, 6],[1,1,1],[2,2,2]])
print(len(x.shape))
print(x.shape[0])
# 遍历张量中的元素
for i in range(x.shape[0]):
    for j in range(x.shape[1]):
        print(x[i, j])

len(x.shape)，维数，一般为二维
x.shape[0]：行数
x.shape[1]: 列数

2
4
tensor(1.)
tensor(2.)
tensor(3.)
tensor(4.)
tensor(5.)
tensor(6.)
tensor(1.)
tensor(1.)
tensor(1.)
tensor(2.)
tensor(2.)
tensor(2.)

进程已结束,退出代码0

torch.ones_like函数和torch.zeros_like函数

返回一个形状与input相同且值全为1的张量。torch.ones_like(input)相当于torch.ones(input.size, dtype=input.dtype，layout=input.layout，device=input.device)

input = torch.rand(4, 6)
print(input)
# 生成与input形状相同、元素全为1的张量
a = torch.ones_like(input)
print(a)
# 生成与input形状相同、元素全为0的张量
b = torch.zeros_like(input)
print(b)

z.backward(torch.ones_like(z))

z.backward(torch.ones_like(z))中的torch.ones_like(z)相当于在对z进
行求导时，对z中的元素进行了求和操作，从而将其转为一个标量。

y.backward(torch.ones_like(x), retain_graph=True)

y.backward(torch.ones_like(x), retain_graph=True)
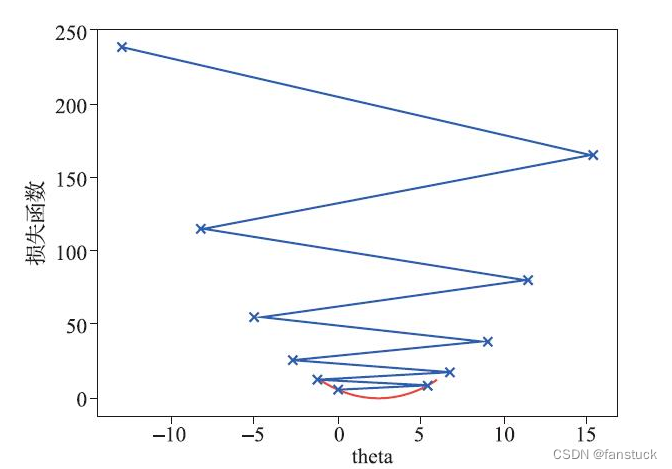
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

torch.autograd.backward

x = torch.tensor(1.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
z = x**2+y
z.backward()
print(z, x.grad, y.grad)

>>> tensor(3., grad_fn=<AddBackward0>) tensor(2.) tensor(1.)

可以z是一个标量，当调用它的backward方法后会根据链式法则自动计算出叶子节点的梯度值。

但是 如果遇到z是一个向量或者是一个矩阵的情况，这个时候又该怎么计算梯度呢？ 这种情况我们需要定义grad_tensor来计算矩阵的梯度。在介绍为什么使用之前我们先看一下源代码中backward的接口是如何定义的：

torch.autograd.backward(
		tensors, 
		grad_tensors=None, 
		retain_graph=None, 
		create_graph=False, 
		grad_variables=None)

• tensor: 用于计算梯度的tensor。也就是说这两种方式是等价的：- torch.autograd.backward(z) == z.backward()
• grad_tensors: 在计算矩阵的梯度时会用到。他其实也是一个tensor，shape一般需要和前面的tensor保持一致。
• retain_graph: 通常在调用一次backward后，pytorch会自动把计算图销毁，所以要想对某个变量重复调用backward，则需要将该参数设置为True
• create_graph: 当设置为True的时候可以用来计算更高阶的梯度
• grad_variables: 这个官方说法是grad_variables’ is deprecated. Use - ‘grad_tensors’ instead.也就是说这个参数后面版本中应该会丢弃，直接使用grad_tensors就好了。

好了，参数大致作用都介绍了，下面我们看看pytorch为什么设计了grad_tensors这么一个参数，以及它有什么用呢？

参数grad_tensors: z.backward(torch.ones_like(x))

原则上，Pytorch不支持对张量的求导，即如果z是张量的话，需要先将其转为标量。

浏览了很多博客，给出的解决方案都是说在求导时，加一个torch.ones_like(z)的参数。

torch.ones_like(z)的作用。简而言之，torch.ones_like(z)相当于在对z进行求导时，对z中的元素进行求和操作，从而将其转为一个标量，便于后续的求导。

x = torch.ones(2,requires_grad=True)
z = x + 2
z.backward()

>>> ...
RuntimeError: grad can be implicitly created only for scalar outputs

本质要得到 z对x求导， 但是已知的是X，Z ；一个矩阵对另一个矩阵求导，才能得到 每个z_partial 对x_partial的导数
其实，可以让sum(z_partial) 对于X求导，对xi 求偏导，就可以得到对应的z_partial
对x_partial的导数，，因为sum(z_partial) 对xi 求偏导，只有包含xi 的那一项在求导，其余与xi 无关的项
对xi求导为0

我们再仔细想想，对z求和不就是等价于z点乘一个一样维度的全为1的矩阵吗？即
,而这个I也就是我们需要传入的grad_tensors参数。(点乘只是相对于一维向量而言的，对于矩阵或更高为的张量，可以看做是对每一个维度做点乘)

import torch

x = torch.ones(2,3,requires_grad=True)
z = 2*x + 2
print(z)
print(z.sum())
# print(z.*torch.ones_like(x))
z.sum().backward()#或者z.backward(torch.ones_like(x)) 效果一样！
print(x.grad)

'''
tensor([[4., 4., 4.],
        [4., 4., 4.]], grad_fn=<AddBackward0>)
tensor(24., grad_fn=<SumBackward0>)
tensor([[2., 2., 2.],
        [2., 2., 2.]])
'''

来个复杂例子z.backward(torch.Tensor([[1., 0]])

x = torch.tensor([2., 1.], requires_grad=True).view(1, 2)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)

z = torch.mm(x, y)
print(f"z:{z}")
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")

>>> z:tensor([[5., 8.]], grad_fn=<MmBackward>)
x.grad: tensor([[1., 3.]])
y.grad: tensor([[2., 0.],
        [1., 0.]])

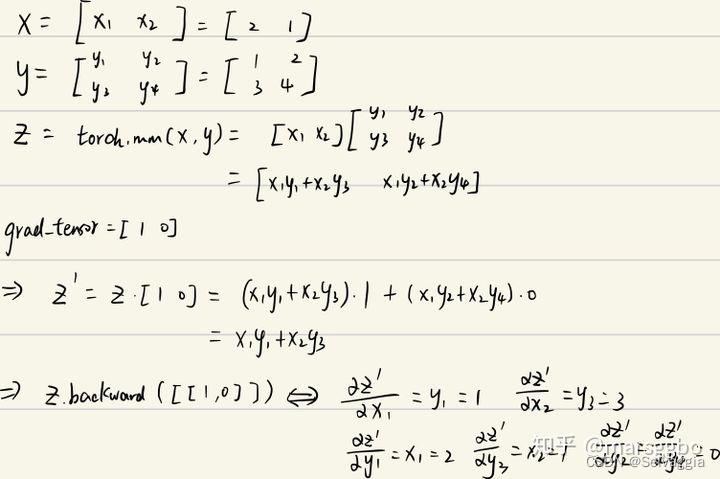
说了这么多，grad_tensors的作用其实可以简单地理解成在求梯度时的权重，因为可能不同值的梯度对结果影响程度不同，所以pytorch弄了个这种接口，而没有固定为全是1。引用自知乎上的一个评论：如果从最后一个节点(总loss)来backward，这种实现(torch.sum(y*w))的意义就具体化为 multiple loss term with difference weights 这种需求了吧
内容来源

看到这里我不由得想，会不会有更复杂的例子呢，万一 输入参数太多多维，导致得到的z不只是一个一维向量，是多维的矩阵，那么就是sum起来或者是点乘一个和z尺寸相同的全1矩阵咯，反正，z是一定是要被处理成一个标量才能进行求导
（原则上，Pytorch不支持对张量的求导，即如果z是张量的话，需要先将其转为标量。）

更复杂例子

import torch

x = torch.tensor(3.,requires_grad=True)
p = torch.ones(2,2,requires_grad=True)

y = x*x
z = 2*y+2*p*p
# [
# [1,1],
# [1,1]
# ]
z.backward(torch.ones_like(z))
# # z = z.sum() # 与下面的torch.sum(z)作用相同，即z中所有元素的和。
# z = torch.sum(z)
# z.backward()
print(x.grad)
print(p.grad)
# print(y.grad) # backward()无法对非叶子节点求导

# 知识点汇总：
# 原则上，Pytorch不支持对张量的求导，即如果z是张量的话，需要先将其转为标量。
# 就这个例子来说，z.backward(torch.ones_like(z))中的torch.ones_like(z)相当于在对z进行求导时，对z中的元素进行了求和操作，从而将其转为一个标量。

pp,张量相乘，对应位置的元素相乘，torch.mul()和 ，广播机制
z = 2y+2p*p，张量相加，广播机制，y这个标量被生生广播 扩维了，
当 z.sum().backward(),求和再对x求导，这个导数就大了不少（广播机制之后再求和，计算过程中标量y维数扩大了四倍，导致z对y的导数也扩大了四倍，夸大了，不合适

这么大，对x求导不太公正啊

实际上，也可以通过 求均值 的形式将其转为标量

z = z.mean() # z中所有元素的均值
z.backward()

该部分来自于此处

retain_graph=True参数

当我们计算梯度时，PyTorch会自动根据计算图反向传播梯度来更新模型参数。但是，当我们的计算图比较复杂，或者需要多次反向传播时，我们可能需要使用retain_graph参数来保存计算图。

retain_graph表示在进行反向传播计算梯度的时候，是否保留计算图。如果设置为True，则计算图将被保留，可以在之后的操作中进行多次反向传播计算。如果为False，则计算图将被清空。这是为了释放内存并防止不必要的计算。

pytorch进行一次backward之后，各个节点的值会清除，这样进行第二次backward会报错，因为虽然计算节点数值保存了，但是计算图结构被释放了，如果加上retain_graph==True后,可以再来一次backward。