前言
其实最优化问题,从小学开始学习数学的时候就可以说已经接触到了,在我印象中有个问题,用一个平底锅煎饼,每次只能放2只饼,煎一只饼要2分钟(正反各用1分钟),煎三只饼要几分钟。这个问题其实已经可以归为最优化问题,我们实际计算出的时间,和真实最节省的时间不断对比去调整煎饼方案,得到时间花费最短的方案,得到最优解。其实这个问题将对象换一下,将煎饼时间换为损失函数,将煎饼换为训练模型,那这个问题就是最优化问题了。根据我们训练出的模型,不论是回归还是分类,总体上总归和原标签是有损失的,要得到更为优秀的模型就要不断的去降低损失值。深度学习系列文章已经把损失函数体系全部都讲解完毕,不论是回归模型、分类模型、聚类模型还是生成模型问题,如果有需要的同学不要错过。此章节将梳理模型训练最优化问题原理和基础理论,以及讲解常用的最优化算法设计和实现。
博主专注建模四年,参与过大大小小数十来次数学建模,理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码,每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛,每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。若你渴望突破数学建模的瓶颈,不要错过笔者精心打造的专栏。愿你能在这里找到你所需要的灵感与技巧,为你的建模之路添砖加瓦。
一文速学-数学建模常用模型
一、最优化问题基础
以文字去说明最优化问题理解起来是十分抽象且难以起到工程化总结归纳的效果,固我们用数学模型来表示,最优化问题的数学模型一般形式可以描述为下面的结构:
- m i n i m i z e f ( x ) minimize f(x) minimizef(x)
- s u b j e c t t o g i ( x ) ≤ 0 , i = 1 , . . . , m subject to g_{i}(x)≤0,i=1,...,m subjecttogi(x)≤0,i=1,...,m
- h j ( x ) = 0 , j = 1 , . . . , p h_{j}(x)=0,j=1,...,p hj(x)=0,j=1,...,p
这里的各个组成部分含义如下:
- f ( x ) f(x) f(x):目标函数,它是我们希望最小化(或最大化)的函数。在最大化问题中,通常将其取负后转化为最小化问题。
- x x x:决策变量,可以是标量或向量。在多维情况下, x x x 表示一个决策向量。
- g i ( x ) g_{i}(x) gi(x):不等式约束函数,它限制了决策变量的可行解必须位于一定的范围内。
- h j ( x ) h_{j}(x) hj(x):等式约束函数,它精确地限制了某些变量的关系。
在没有约束的情况下,最优化问题可以简化为仅最小化(或最大化)目标函数 f ( x ) f(x) f(x)。可能讲到这里大家一看到数学公式又犯懵了,我们再来这么理解:
想象你在玩一款视频游戏,你的目标是得到尽可能多的分数(这就像是你的目标函数 f ( x ) f(x) f(x)),分数是由你的游戏行为(决策变量 x x x)决定的。但是,游戏中有一些规则:
- 有一些任务你必须避免做到(这就是不等式约束 g i ( x ) ≤ 0 g_{i}(x)≤0 gi(x)≤0,比如说,你的角色不能掉入陷阱里,否则你会失分或者游戏结束。
- 另外,有一些必须完成的任务(等式约束 h j ( x ) = 0 ℎ_{j}(x)=0 hj(x)=0,比如说,你需要收集所有的金币才能过关。.
在游戏的可行区域(就是你能在游戏规则下行动的空间)内,你需要找到最好的策略来完成关卡并且得到最高分。这就是你在最优化问题中尝试完成的任务:在一定的规则内,找到最佳的解决方案。在现实世界的问题中,你可能会寻找成本最低的生产策略、最快的路线或者最有效的广告投放方案,而这些都需要在特定的限制和规则下进行。
在不同的领域,这个一般形式的最优化问题可能有更具体的变体。例如:
- 线性规划(Linear Programming, LP):目标函数和所有约束都是线性的。
- 非线性规划(Nonlinear Programming, NLP):目标函数或某些约束是非线性的。
- 整数规划(Integer Programming):所有或部分决策变量被限制为整数。
- 混合整数线性规划(Mixed Integer Linear Programming, MILP):某些决策变量是整数,且目标函数和约束都是线性的。
- 动态规划(Dynamic Programming):用于多阶段决策过程优化的方法,可以分解为一系列相互关联的子问题。
理解了以上最优化算法的大体框架之后,我们需要开始学习一些更细致化的理论知识。从最优化算法的建模步骤开始,我们来逐渐拆解建模过程:
- 定义问题:明确目标函数,变量以及任何可能的约束条件。
- 选择合适的优化方法:根据问题的特性,选择一个有效的优化算法。
- 初始化参数:为变量选择一个初始值。
- 迭代优化:通过迭代过程改进变量,以最小化目标函数。
- 终止条件:设定一个停止标准,例如迭代次数、目标函数的变化量或计算资源限制。
1.目标函数
目标函数(或成本函数、损失函数)是最优化问题的核心,它是需要最大化或最小化的函数。在机器学习中,目标函数通常衡量模型预测值与实际值之间的差异,因为之前有详细讲过各个模型的类型函数,这里不过多讲解:
2. 变量
在最优化问题中,变量是决定目标函数值的因素。在机器学习模型中,变量通常指模型的参数,如权重和偏置。通过损失函数的值不断的调整变量权重,就是优化过程。
3.约束条件
在最优化问题中,约束条件定义了解决方案必须遵守的规则。这些规则可以限制解决方案的取值范围或指定某些变量之间的关系。约束条件通常分为两类:等式约束和不等式约束。
3.1等式约束
等式约束指定了变量之间必须满足的精确关系。举个例子,如果我们正在设计一个小工具,其中一个部件的长度加上另一个部件的两倍长度必须总共等于10厘米,那么这就是一个等式约束。数学表达为: h j ( x ) = 0 h_{j}(x)=0 hj(x)=0,其中 h j ( x ) h_{j}(x) hj(x)是一个函数,它描述了变量 x x x之间的关系,而 j j j只是一个索引,用于当有多个等式约束时进行区分。
3.2不等式约束
不等式约束定义了变量的取值范围,而不是确切的值。例如,如果你有一个背包,它的承重限制是20公斤,那么你放入背包的物品总重量就受到了一个不等式约束。数学表达为: g i ( x ) ≤ 0 g_{i}(x)≤0 gi(x)≤0,其中 g i ( x ) g_{i}(x) gi(x)表示变量 x x x与允许的极限值之间的差距, i i i是约束的索引,用于区分多个不等式约束。
3.3约束条件的重要性
约束条件在最优化问题中至关重要,因为它们确保了解决方案是可行的。在没有约束的情况下,最优化问题可能会导致不现实或不可行的解决方案。例如,在工程设计问题中,如果没有考虑材料的强度或成本,可能会得到理论上效率最高,但实际上无法构建或成本过高的设计。
4.最优化算法
最优化算法是一系列解决最优化问题的数学方法,它们的目标是在给定的条件下寻找最佳的决策变量值。这些变量值可以最小化或最大化一个目标函数。也就是找到最优权重的 x x x,这里简单介绍一下各类最优化算法:
4.1梯度下降(Gradient Descent)
梯度下降是最常见的最优化算法之一,特别是在机器学习领域。这种方法通过计算目标函数的梯度来找到函数值下降最快的方向。然后,它按照这个方向调整变量值,以此来减少函数值。梯度下降分为几种类型:
- 批梯度下降:在每一步使用所有数据计算梯度。
- 随机梯度下降(SGD):在每一步只使用一个数据样本来计算梯度。
- 小批量梯度下降:介于批梯度下降和随机梯度下降之间,它在每一步使用一小批数据来计算梯度。
4.2牛顿法和拟牛顿法
这些方法利用了目标函数的二阶导数信息(即海森矩阵),提供了更快的收敛速率,特别是接近最优解时。拟牛顿法是一类不需要显式计算海森矩阵的方法,例如BFGS和L-BFGS,它们适用于大规模问题的优化。
4.3动量方法
动量方法在SGD的基础上增加了一个动量项,有助于加速SGD在相关方向上的导数,并抑制震荡,从而加快收敛速度。
4.4Adam(Adaptive Moment Estimation)
Adam结合了动量方法和RMSprop的优点。它计算了梯度的一阶矩(即平均值)和二阶矩(即未中心化的方差),然后用这些矩来调整每个参数的学习率。
4.5约束最优化
在有约束的情况下,拉格朗日乘数法是处理等式约束的经典方法。对于不等式约束,可以使用KKT(Karush-Kuhn-Tucker)条件,它是拉格朗日乘数法的一种推广。
4.6启发式和元启发式算法
对于某些复杂的或非凸优化问题,传统的梯度方法可能不适用或效率较低。启发式算法,如遗传算法、粒子群优化(PSO)和模拟退火,提供了替代的全局搜索策略。
4.7贝叶斯优化
贝叶斯优化是一种基于概率模型的全局优化策略,特别适用于那些目标函数评估代价很高的问题。它使用高斯过程来建立目标函数的代理模型,并使用这个模型来指导搜索。
5.凸性
凸性是最优化和数学分析中的一个核心概念。它描述了一个数学对象(如集合或函数)的形状特性。当我们说一个集合或函数是凸的,我们在描述其内部的结构和与其相关的直观几何属性。
5.1凸集
一个集合被称为凸集,如果它内部的任意两点之间的直线段都完全包含在该集合内部。形式化地说,一个集合
C
C
C是凸的,如果对于任意两点
x
,
y
∈
C
x,y∈C
x,y∈C 和任意
θ
θ
θ满足
0
≤
θ
≤
1
0≤θ≤1
0≤θ≤1,以下条件成立:
θ
x
+
(
1
−
θ
)
y
∈
C
θx+(1-θ)y∈C
θx+(1−θ)y∈C
5.2凸函数
一个函数
f
:
R
n
−
>
R
f:R^n->R
f:Rn−>R被称为凸函数,如果它的定义域是一个凸集,并且对于定义域内的任意两点x和y以及任意
θ
θ
θ满足
0
≤
θ
≤
1
0≤θ≤1
0≤θ≤1,以下不等式成立:
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
f(θx+(1-θ)y)≤θf(x)+(1-θ)f(y)
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
直观上,这意味着函数的图形之上的任意一点和图形上任意两点连线之间的区域也在图形之上。这也意味着凸函数的局部最小值也是全局最小值。
函数 f ( x ) = x 2 f(x)=x^2 f(x)=x2是一个典型的凸函数。我们可以观察到对于定义域内的任意两点,函数图像上的线段始终位于函数曲线的上方,这是凸函数的关键特性。在整个定义域内,这个函数的任何局部最小值也是全局最小值,而对于这个特定的函数,最小值在 x = 0 x=0 x=0处取得。
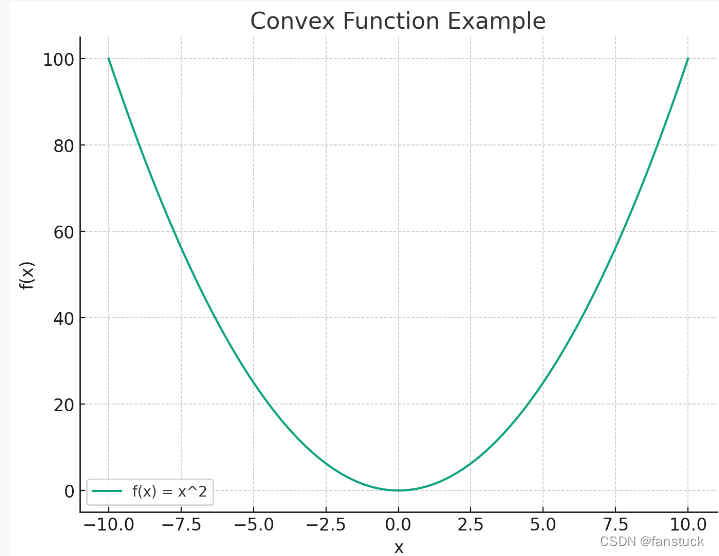
5.3凸性的重要性
凸性在最优化问题中非常重要,因为它保证了最优化问题具有良好的数学性质:
- 全局最优解:凸优化问题的任何局部最优解也是全局最优解。
- 优化算法:针对凸问题的优化算法通常更简单,更容易分析,并且更容易实现。
- 稳定性:凸问题的解通常对问题数据的微小变化具有稳定性。
5.4凸优化
凸优化是研究凸函数或凸集合上的优化问题的一个子领域。由于凸问题的特殊性质,凸优化通常比一般的优化问题要容易解决得多。
5.5判断凸性
对于凸集,判断凸性相对直观。而对于凸函数,判断一个函数是否为凸可以通过计算其二阶导数(如果存在)来完成。如果函数的二阶导数是正的(对于一维函数)或者海森矩阵是半正定的(对于多维函数),那么这个函数是凸函数。
6.导数与梯度
在最优化问题中,导数和梯度是核心的数学概念,用来描述目标函数如何随变量变化而变化,并指导我们如何找到函数的最小值或最大值。
6.1导数(Derivative)
导数是单变量微积分中的基本概念,它描述了函数在某一点处随变量的变化率。对于函数 f ( x ) f(x) f(x),在点 x x x处的导数通常表示为 f ′ ( x ) f'(x) f′(x)或 d f d x \frac{df}{dx} dxdf。导数告诉我们函数在这一点的斜率,以及函数值是增加还是减少。如果导数为正,那么函数在这一点上随着变量增加而增加;如果导数为负,函数随变量增加而减少。如果导数为零,那么这一点可能是函数的局部极大值、局部极小值或鞍点。在最优化中,我们通常寻找使导数为零的点,因为这些点是潜在的最优点。
6.2梯度
梯度下降算法基于的思想是:要找到函数的最小值,最好的方法是沿着该函数的下降方向探寻。对此我们需要明白代表函数变化快慢的导数以及偏导数,在此基础上我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。梯度与方向导数有一定的关联性,在微积分里面,对多元函数的参数求delta偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
纯数理化的知识可能比较难懂,我们可以结合实际例子来了解:一座高度在 ( x , y ) (x,y) (x,y)点是 H ( x , y ) H(x,y) H(x,y)的山。 H H H这一点的梯度是在该点坡度(或者说斜度)最陡的方向。梯度的大小告诉我们坡度到底有多陡。
梯度也可以告诉我们一个数量在不是最快变化方向的其他方向的变化速度。再次结合山坡的例子。可以有条直接上山的路其坡度是最大的,则其坡度是梯度的大小。也可以有一条和上坡方向成一个角度的路,例如投影在水平面上的夹角为60°。则,若最陡的坡度是40%,这条路的坡度小一点,是20%,也就是40%乘以60°的余弦。
这个现象可以如下数学的表示。山的高度函数
H
H
H的梯度点积一个单位向量给出表面在该向量的方向上的斜率。这称为方向导数。梯度的方向是函数在该点增长最快的方向,而梯度的大小(模)表示在该方向上函数增长的速率。在最优化问题中,我们通常希望找到函数的全局最小值(对于最小化问题)。通过计算梯度并沿着梯度的反方向(即最陡下降方向)迭代更新变量值,我们可以逼近函数的最小值。
那么了解了以上最优化问题的解答基础之后,可以开始逐步关联这些相关理论,学习一些最优化算法来达到融会贯通。
二、最优化算法计算原理和实现
1.梯度下降法(Gradient Descent)
梯度下降算法(GradientDescent Optimization)是常用的最优化方法之一,“最优化方法”属于运筹学方法,是指在某些约束条件下,为某些变量选取哪些值,可以使得设定的目标函数达到最优问题。最优化方法有很多种,常见的有梯度下降法、牛顿法、共轭梯度法,等等。
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
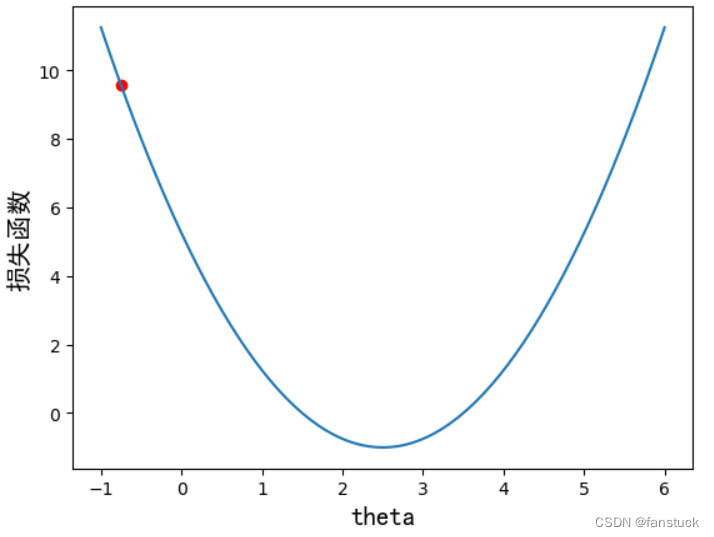
plot_x = np.linspace(-1,6,141)#从-1到6选取141个点
plot_y = (plot_x - 2.5)**2 -1 #二次方程的损失函数
plt.scatter(plot_x[5],plot_y[5],color='r') #设置起始点,颜色为红色
plt.plot(plot_x,plot_y)
#设置坐标轴名称
plt.xlabel('theta',fontproperties='simHei',fontsize=15)
plt.ylabel('损失函数',fontproperties='simHei',fontsize=15)
plt.show()
上述代码画出损失函数示意图,x轴代表的是参数theta,y轴代表的是损失函数的值(即Loss值),曲线y代表的是损失函数。我们的目标是希望通过大量的数据训练和调整参数theta,使得损失函数的值最小,可以通过求导数的方式,达到二次方程的最小值点,使得导数为0即可。梯度下降中有个比较重要的参数:学习率eta,它控制模型寻找最优解的速度。
首先定义损失函数以及导数:
def J(theta): #损失函数
return (theta-2.5)**2-1
def dJ(theta): #损失函数的导数
return 2*(theta-2.5)
通过matplotlib绘制梯度下降迭代过程
theta = 0.0 #初始点
theta_history = [theta]
eta = 0.1 #步长
epsilon = 1e-8 #精度问题或者eta的设置无法使得倒数为0
while True:
gradient = dJ(theta)
last_theta = theta #先记录下上一个theta的值
theta = theta - eta * gradient #得到一个新的theta
theta_history.append(theta)
if(abs(J(theta)-J(last_theta))<epsilon):
break #当两个theta值非常接近的时候,终止循环
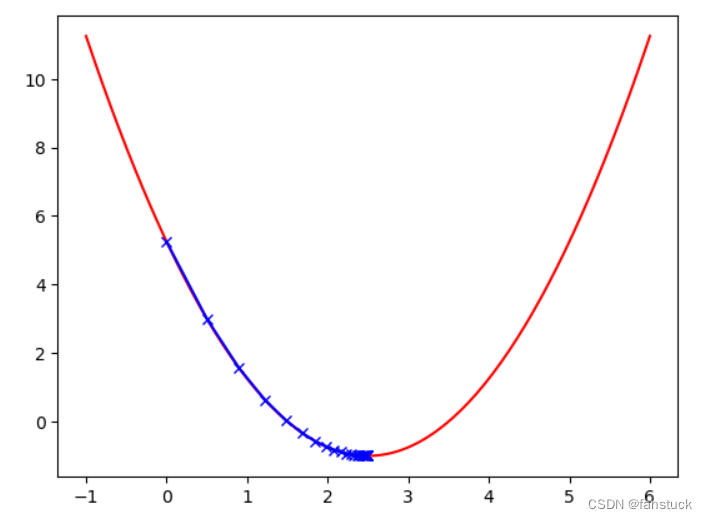
plt.plot(plot_x,J(plot_x),color='r')
plt.plot(np.array(theta_history),J(np.array(theta_history)),color='b',marker='x')
plt.show() #一开始的时候导数比较大,因为斜率比较陡,后面慢慢平缓了
print(len(theta_history)) #一共走了46步
学习率对梯度下降法的影响
首先看两个例子,一个学习率为0.01,另一个为0.8
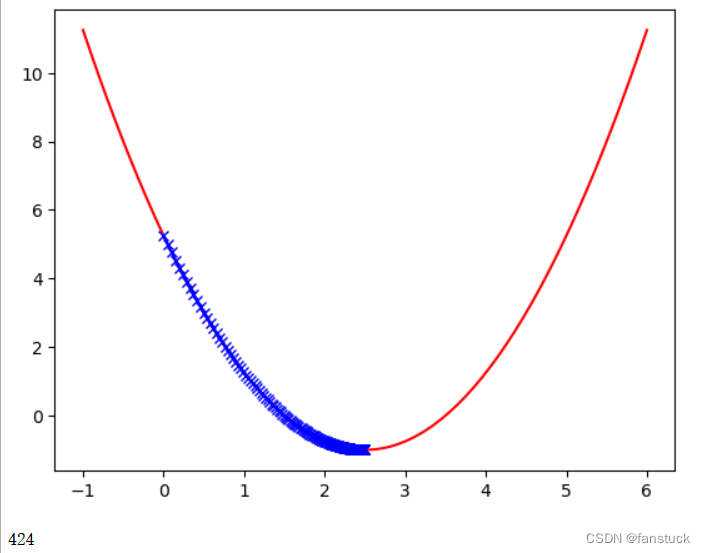
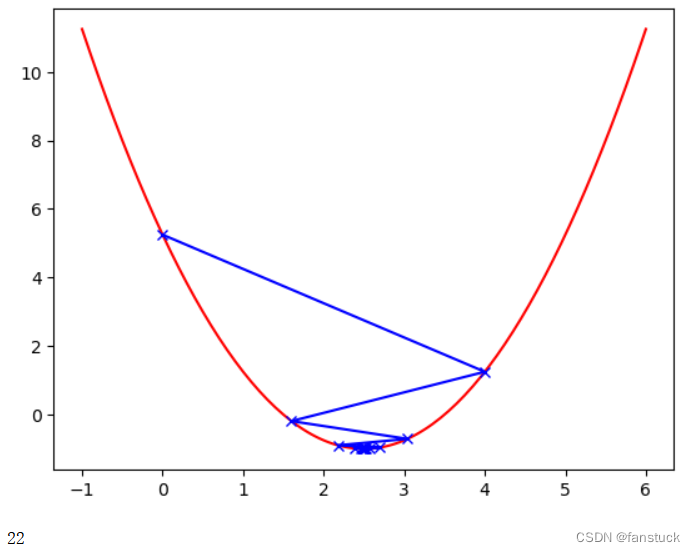
第一个例子很明显学习的速度变慢了,第二个例子蓝色的步长在损失函数之间发生了跳跃,不过在跳跃的过程中,损失函数的值依然在不断地变小,步数是22步,因此学习率为0.8时,优化过程的时间缩短。当学习率为1.1时:
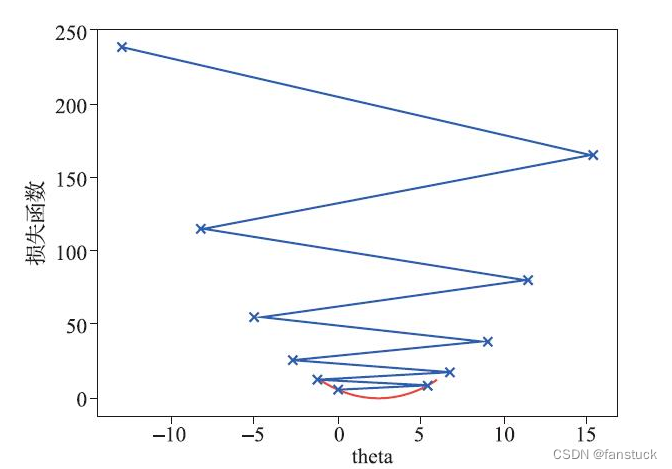
一元二次函数不收敛。学习率是一个需要认真调整的参数,过小会导致收敛过慢,而过大又可能导致模型不收敛。
2.随机梯度下降(Stochastic Gradient Descent, SGD)
随机梯度下降(Stochastic Gradient Descent,简称SGD)是一种用于最优化目标函数的算法,尤其是在机器学习和深度学习中用于最小化损失函数。它是梯度下降算法的一种变体,主要区别在于SGD每次更新参数时只使用一个样本或一个小批量样本来计算梯度,而不是像标准梯度下降算法那样使用整个数据集。
SGD的基本步骤如下:
- 随机选择:从数据集中随机选择一个样本(或一小批样本)。
- 计算梯度:计算选中样本在当前参数下损失函数的梯度。
- 更新参数:根据梯度和学习率更新模型参数。
伪代码如下:
for each epoch:
Shuffle the dataset
for each sample in the dataset:
gradient = compute_gradient(sample, parameters)
parameters = parameters - learning_rate * gradient
这种每次只使用一个样本的更新方式使SGD特别适合大规模数据集的训练。SGD能更快地进行参数更新,因为它不需要在每次迭代中查看所有数据。此外,随机性有助于SGD跳出局部最小值,增加找到全局最小值的可能性。然而,SGD的缺点是它的更新可能会很嘈杂,导致目标函数的收敛路径变得非常波动。为了克服这一点,通常会随着时间逐渐减小学习率,或者使用SGD的变体,如带动量的SGD或者Adam优化器。
import numpy as np
# 假设我们有一个简单的线性关系 y = 2x + 3 + noise
# 我们将生成一些样本数据来模拟这一关系
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 * x + 3 + np.random.randn(100, 1) * 0.1
# 初始化参数
w = np.random.randn(1)
b = np.random.randn(1)
# 学习率
learning_rate = 0.1
# 进行100次迭代
for epoch in range(100):
# 在所有样本中随机选择一个
idx = np.random.randint(100)
x_sample = x[idx]
y_sample = y[idx]
# 计算梯度
gradient_w = -2 * x_sample * (y_sample - (w * x_sample + b))
gradient_b = -2 * (y_sample - (w * x_sample + b))
# 更新参数
w = w - learning_rate * gradient_w
b = b - learning_rate * gradient_b
# 输出学习到的参数值
print(f"Learned linear function: y = {w[0]}x + {b[0]}")
输出:Learned linear function: y = 2.127594940622086x + 2.941043061188159
在实际的深度学习应用中,梯度的计算会更复杂,并且通常会使用自动微分库(如TensorFlow或PyTorch)来计算梯度。此外,为了提高收敛速度和稳定性,通常会使用SGD的变体,如带动量的SGD、Adam或RMSprop等。
3.Adam(Adaptive Moment Estimation)
Adam(Adaptive Moment Estimation)算法是一种用于深度学习中的优化算法,它结合了Momentum(动量)和RMSprop(均方根传播)的思想。Adam 通过计算梯度的一阶矩(即均值)和二阶矩(即未中心化的方差)估计来自适应地调整每个参数的学习率。
Adam 算法的关键特点:
- 动量:考虑了过去梯度的指数衰减平均,帮助加速学习过程。
- 自适应学习率:为每个参数计算梯度平方的指数衰减平均,调整学习率。
- 偏差校正:对一阶矩和二阶矩的估计进行校正,以防止它们在训练初期(接近于0)的偏差。
Adam 算法的更新规则:
对于每个参数 θ,在每个时间步 t:
- 计算梯度 g t g_{t} gt。
- 更新有偏一阶矩估计: m t = β 1 ∗ m t − 1 + ( 1 − β 1 ) ∗ g t m_{t}=β_{1}*m_{t-1}+(1-β_{1})*g_{t} mt=β1∗mt−1+(1−β1)∗gt
- 更新有偏二阶矩估计: v t = β 2 ∗ v t − 1 + ( 1 − β 2 ) ∗ g t 2 v_{t}=β_{2}*v_{t-1}+(1-β_{2})*g^2_{t} vt=β2∗vt−1+(1−β2)∗gt2
- 计算偏差校正后的一阶矩估计: m t ^ = m t 1 − β 2 t \hat{m_{t}}=\frac{m_{t}}{1-β^t_{2}} mt^=1−β2tmt
- 计算偏差校正后的二阶矩估计: v t ^ = v t 1 − β 2 t \hat{v_{t}}=\frac{v_{t}}{1-β^t_{2}} vt^=1−β2tvt
- 更新参数: θ t + 1 = θ t − α ∗ m t ^ / ( v t ^ + c ) θ_{t+1}=θ_{t}-α*\hat{m_{t}}/(\sqrt{\hat{v_{t}}+c}) θt+1=θt−α∗mt^/(vt^+c)
其中, α α α是学习率, β 1 β_{1} β1和 β 2 β_{2} β2是衰减率参数,通常取值接近1,ϵ 是为了保持数值稳定性而加入的一个小常数。下面我们来实现Adam算法:
import numpy as np
# 假设我们有一个简单的线性关系 y = 2x + 3 + noise
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 * x + 3 + np.random.randn(100, 1) * 0.1
# 初始化参数
params = np.random.randn(2)
m, v = np.zeros(2), np.zeros(2)
# Adam 参数
alpha, beta1, beta2, epsilon = 0.01, 0.9, 0.999, 1e-8
# 运行Adam优化
for t in range(1, 1001):
# 随机获取样本
idx = np.random.randint(100)
x_i, y_i = x[idx], y[idx]
# 计算梯度
grads = 2 * np.array([x_i * (params[0] * x_i + params[1] - y_i), (params[0] * x_i + params[1] - y_i)]).squeeze()
# 更新一阶和二阶矩估计
m = beta1 * m + (1 - beta1) * grads
v = beta2 * v + (1 - beta2) * (grads ** 2)
# 计算偏差校正后的估计
m_hat = m / (1 - beta1 ** t)
v_hat = v / (1 - beta2 ** t)
# 更新参数
params -= alpha * m_hat / (np.sqrt(v_hat) + epsilon)
# 输出学习到的参数值
print(f"Learned parameters: {params}")
代码执行成功,并且经过Adam优化算法的迭代,Learned parameters: [2.68152662 2.64279962],我们得到了参数值[2.68152662,2.64279962]。
这意味着学习到的线性模型大致为 y = 2.68 x + 2.64 y=2.68x+2.64 y=2.68x+2.64,接近于我们模拟数据的真实关系。
4.遗传算法(Genetic Algorithms, GAs)
遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
遗传算法的基本步骤:
- 初始化:随机生成一开始的种群。种群由一系列候选解组成,每个候选解(个体)通常是问题解空间中的一个点。
- 评估:计算种群中每个个体的适应度(Fitness),适应度反映了个体解决问题的能力。
- 选择(Selection):根据个体的适应度选择较优秀的个体进行繁殖。常用的选择方法有轮盘赌选择、锦标赛选择等。
- 交叉(Crossover):随机选取一对个体作为父母,按照某种规则交换它们的部分基因,产生新的个体(子代)。这个过程模拟了生物的交配。
- 变异(Mutation):以较小的概率随机改变个体中的某些基因,这增加了种群的多样性,有助于算法跳出局部最优解。
- 替换:新一代的个体替换掉旧的个体,形成新的种群。这可能会完全替换,或是部分替换。
- 终止:重复以上步骤,直到满足某个终止条件,比如达到了最大迭代次数,或者种群已经足够优化。
下面我们来简单实现遗传算法:
import numpy as np
# 目标函数
def fitness_function(x):
return np.sum(x**2)
# 初始化
def initialize_population(size, n):
return np.random.rand(size, n)
# 选择
def selection(pop, fitness):
idx = np.argsort(fitness)
return pop[idx[:int(len(idx)/2)]]
# 交叉
def crossover(parents, n_children):
children = []
for _ in range(n_children):
parent1, parent2 = parents[np.random.choice(len(parents), 2, replace=False)]
child = parent1[:len(parent1)//2]
child = np.concatenate((child, parent2[len(parent2)//2:]))
children.append(child)
return np.array(children)
# 变异
def mutation(children, mutation_rate=0.01):
for child in children:
if np.random.rand() < mutation_rate:
idx = np.random.choice(len(child))
child[idx] = np.random.rand()
return children
# 遗传算法
def genetic_algorithm(fitness_function, n_iterations, population_size, n_variables):
pop = initialize_population(population_size, n_variables)
best_fit = float('inf')
best_solution = None
for _ in range(n_iterations):
fitness = np.apply_along_axis(fitness_function, 1, pop)
best_idx = np.argmin(fitness)
if fitness[best_idx] < best_fit:
best_fit = fitness[best_idx]
best_solution = pop[best_idx]
selected = selection(pop, fitness)
children = crossover(selected, len(pop) - len(selected))
children = mutation(children)
pop = np.concatenate((selected, children))
return best_solution, best_fit
# 使用遗传算法
best_solution, best_fitness = genetic_algorithm(
fitness_function,
n_iterations=100,
population_size=50,
n_variables=5
)
print(f"Best solution: {best_solution}")
print(f"Best fitness: {best_fitness}")
在上述代码中,目标函数 fitness_function 被定义为 np.sum(x**2),这意味着它会计算一个向量 x 中所有元素的平方和。在遗传算法的上下文中,该函数作为一个适应度函数,其目的是最小化这个函数值。因此,遗传算法在这里的目标是找到一个向量 x,使得 x 中元素的平方和尽可能小。由于 x 中的元素都是非负的(由于是平方),因此最小化平方和实际上等同于找到接近零的向量。上述代码执行结果为:
Best solution: [0.02683969 0.07490378 0.34308792 0.01243034 0.06044091]
Best fitness: 0.12784788404801556
遗传算法通过模拟自然选择的过程来逐步改进种群中个体的质量,最终找到能够产生最低适应度(在这个例子中,即最小的平方和)的解。代码中的 best_solution 就是算法找到的最佳解,而 best_fitness 是这个解的适应度值,即目标函数的最小值。
itness_function被定义为np.sum(x**2),这意味着它会计算一个向量 x中所有元素的平方和。在遗传算法的上下文中,该函数作为一个适应度函数,其目的是最小化这个函数值。因此,遗传算法在这里的目标是找到一个向量x,使得 x中元素的平方和尽可能小。由于x` 中的元素都是非负的(由于是平方),因此最小化平方和实际上等同于找到接近零的向量。上述代码执行结果为:
Best solution: [0.02683969 0.07490378 0.34308792 0.01243034 0.06044091]
Best fitness: 0.12784788404801556
遗传算法通过模拟自然选择的过程来逐步改进种群中个体的质量,最终找到能够产生最低适应度(在这个例子中,即最小的平方和)的解。代码中的 best_solution 就是算法找到的最佳解,而 best_fitness 是这个解的适应度值,即目标函数的最小值。
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
以上就是本期全部内容。我是fanstuck ,有问题大家随时留言讨论 ,我们下期见。