TensorFlow2的建模流程:疫情发展趋势分析
- 时间序列简介
- 基本概念
- 平稳性
- 白噪声
- 随机游走(Random Walk)
- 识别一个时间序列
- Augmented Dickey-Fuller Test(ADF)
- Kwiatkowski-Phillips-Schmidt-Shin Test(KPSS)
- 时间序列模型预测准确度的衡量
- 衡量预测准确度的常用统计量
- 使用样本外数据验证步骤
- 时间序列数据示例
- 单变量时间序列数据集
- 多元时间序列数据集
- 简要回顾ARIMA时间序列模型
- 识别差分项的原则
- 识别自回归或者预测误差项的原则
- 识别模型的季节性
- 循环神经网络与时间序列模型
- 长短时记忆网络(LSTM)
- 循环神经网络的变种
- 双向循环神经网络和深层循环神经网络
- 双向循环神经网络
- 深层循环神经网络
- 循环神经网络的dropout
- 时间序列数据建模实战
- 数据准备
- 定义模型
- 训练模型
- 评估模型
- 使用模型
- 保存模型
- 参考资料
时间序列简介
时间序列是在商业数据或工程数据中经常出现的一种数据形式,是以时间为次序排列。用来描述和计量一系列过程或者行为的数据的统称。一般研究的时间序列数据有两种类型。最常见的是跟踪单一的计量数据随时间变化的情况,即每个时间点上收集的数据是一个一维变量,这种是最常见的,通常的时间序列默认就是这种数据。另一种时间序列是多个对象或者多个维度的计量数据随时间变化的情况,即每个时间点上收集的数据是一个多维变量,这种一般也被称为纵向数据(Longitudinal Data)。
基本概念
平稳性
有效的时间序列分析依赖于几个核心概念。其中最核心的概念是平稳性(Stationarity)。在分析时间序列数据时,需要考虑这个时间序列反映的随机过程是否稳定。如果一个时间序列不稳定,则说明其来自的总体在发生变化,那么在忽略这种情况下进行的分析并不有效,特别是不能有效地应用于对未来事件的预测。
时间序列数据
y
t
,
t
=
1
,
.
.
.
,
T
y_t,t=1,...,T
yt,t=1,...,T的稳定性定义有多种角度,其中使用最广泛的就是数学上讲的弱平稳性,其定义如下:
y
t
的期望值
E
(
y
t
)
不是时间
t
的函数:
E
(
y
t
)
=
μ
y_t\text{的期望值}E(y_t)\text{不是时间}t\text{的函数:}E(y_t)=\mu
yt的期望值E(yt)不是时间t的函数:E(yt)=μ
y
s
和
y
t
之间的协方差只是时间单位差绝对值
∣
s
−
t
∣
的函数:
C
o
v
(
y
s
,
y
t
)
=
C
o
v
(
y
s
+
z
,
y
t
+
z
)
y_s\text{和}y_t\text{之间的协方差只是时间单位差绝对值}|s-t|\text{的函数}:Cov(y_s,y_t)=Cov(y_{s+z},y_{t+z})
ys和yt之间的协方差只是时间单位差绝对值∣s−t∣的函数:Cov(ys,yt)=Cov(ys+z,yt+z)
具体来讲就是,在弱平稳性的假设条件下,期望值不依赖于时间而变化,而协方差只是两个序列时间间隔的区间的函数。第二条假设隐含意思就是弱平稳性的时间序列方差恒定(Homoscedasticity)。
比弱平稳性更强的数学假设条件为强平稳性,也称为严格平稳性。这一假设条件下要求随机变量
y
t
y_t
yt的整个概率分布不随时间的改变而变化。但是在一般的应用场景下,满足弱平稳性条件已经能够适用于大多数模型。
白噪声
第二个概念为白噪声(White Noise)。白噪声是研究随机过程中经常出现的概念,是联系横截面数据(Cross Sectional Data)和纵向数据的纽带。严格来讲,白噪声是具有独立同分布(i.i.d)的数据序列,即没有特定随时间变化特征的满足平稳性条件的数据。
另一种满足平稳性条件的时间序列数据类型是自回归过程。白噪声数据在时间序列研究中之所以重要是因为所有时间序列的技术都要将一组数据通过一系列过程尽量变为一个白噪声数据,这一系列过程就被称为滤子。
白噪声数据的特点是对其的点预测及其方差不依赖于想要预测到多远,而只与样本数据的均值和方差有关。举个例子,如果有暴燥声过程 y t , t = 1 , . . . , T y_t,t=1,...,T yt,t=1,...,T,而要预测 T + s T+s T+s期未来数据的大小,则其最优期望值为样本均值 y ˉ \bar{y} yˉ,而预测的 α \alpha α置信区间为 y ˉ ± t T − 1 , 1 − α / 2 ( 1 + 1 / T ) s y \bar{y}\pm t_{T-1,1-\alpha/2}\sqrt{(1+1/T)s_y} yˉ±tT−1,1−α/2(1+1/T)sy其中 s y s_y sy为样本方差根,而 t T − 1 , 1 − α / 2 t_{T-1,1-\alpha/2} tT−1,1−α/2则是自由度为 T − 1 T-1 T−1的T-分布统计量 α \alpha α百分位下的对应值,通常95%百分位下约为2.
随机游走(Random Walk)
白噪声时间序列的累加和就构成一个随机游走时间序列,举个例子,如果
z
t
,
t
=
1
,
.
.
.
,
T
z_t,t=1,...,T
zt,t=1,...,T是一组白噪声序列,则
y
t
=
∑
1
t
z
t
,
t
≥
1
y_t=\sum_{1}^tz_t, t\ge 1
yt=∑1tzt,t≥1构成一组随机游走序列。
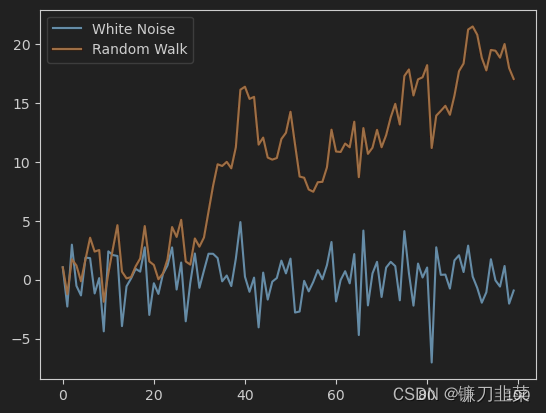
举例:一个均值为0.1,标准差为2的100个时间点的白噪声,及其对应的随机游走时间序列。
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1234)
z = np.random.normal(0.1, 2, 100)
y = np.cumsum(z)
fig, ax1 = plt.subplots()
plt.plot(z, label='White Noise')
plt.plot(y, label='Random Walk')
plt.legend()
plt.show()
mean1 = np.round(np.mean(y[:20]),4)
mean2 = np.round(np.mean(y[-20:]),4)
std1 = np.round(np.std(y[:20]),4)
std2 = np.round(np.std(y[-20:]),4)
print(f'前20个数据点的均值为{mean1},标准差为{std1}')
print(f'后20个数据点的均值为{mean2},标准差为{std2}')
输出结果:
前20个数据点的均值为1.4326,标准差为1.6367
后20个数据点的均值为17.5324,标准差为2.7009
从图中可以看出随机游走时间序列的几个特点。首先是这种时间序列数据是非平稳的,其均值和方差都随着时间而变化。对这个随机游走时间序列取一阶差分作为滤子,过滤后的时间序列则为上例中的白噪声序列。
随机游走模型是一类非常重要的时间序列模型,因为其为对应的白噪声时间序列的累加和,所以每个时间点上该变量的期望和方差分别为:
E
(
y
t
)
=
y
0
+
t
μ
E(y_t)=y_0+t\mu
E(yt)=y0+tμ
V
a
r
(
y
t
)
=
t
σ
2
Var(y_t)=t\sigma^2
Var(yt)=tσ2其中
μ
,
σ
2
\mu, \sigma^2
μ,σ2是对应的白噪声序列的期望均值和方差,而
y
0
y_0
y0则为这个白噪声随机变量在初始时间的某个具体实现。只要这个均值大于0,则随机游走时间序列表现为总体上一个不断增长的曲线;而如果这个均值小于0,则随机游走时间序列表现为一个总体上不断下降的曲线。另外,随机游走时间序列的方差也是时间的线性函数。
可见,随机游走模型是一个随时间变动的线性模型,相应地,如果要对一个随机游走时间序列进行预测,则其公式为
y
T
+
s
=
y
T
+
s
μ
^
±
2
σ
^
s
y_{T+s}=y_T+s\hat{\mu}\pm 2\hat{\sigma}\sqrt{s}
yT+s=yT+sμ^±2σ^s其中,
y
T
y_T
yT是已知随机游走时间序列的末尾值,
s
s
s是要预测的未来时间间隔,
μ
^
,
σ
^
\hat{\mu}, \hat{\sigma}
μ^,σ^则分别是对应的白噪声过程的期望均值和标准差的估计值,通常为样本的均值和标准差。
可以看到,对于白噪声和随机游走两种不同的时间序列的预测有不同的模型,问题是该怎么识别一个已知的事件时间序列是平稳的还是一个随机行走时间序列呢?
识别一个时间序列
首先,要识别一个时间序列是否是平稳的,通过检验单位根的方法,常见的有以下几种(Python的StatsModels包):
Augmented Dickey-Fuller Test(ADF)
ADF是最常见的单位根检验方法。其默认假设待检验的时间序列是不平稳的,如果得到的统计量的p值较大,则说明这个时间序列是不平稳的,如果p较小,则说明这个时间序列是平稳的。假如我们用5%作为p值的界限,那么如果ADF统计量的p值大于0.05,则表明时间序列是不平稳的,需要做差分运算,一直到检验结果表明是平稳的为止。
在Python中可以使用statsModels的tsa.stattools.adfuller(x)函数来检验时间序列X的平稳性。
Kwiatkowski-Phillips-Schmidt-Shin Test(KPSS)
KPSS检验是一种较新的检验方式,其默认假设待检验的时间序列是平稳的,如果得到的统计量p值较大,则说明这个时间序列是平稳的;反之是不平稳的。
在Python中使用StatsModels库的tsa.stattools.kpss(x)函数来检验时间序列的平稳性。
时间序列模型预测准确度的衡量
衡量预测准确度的常用统计量
(1)平均误差(Mean Error, ME)
M
E
=
1
T
2
∑
t
=
T
1
+
1
T
1
+
T
2
e
t
ME=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}e_t
ME=T21t=T1+1∑T1+T2et平均误差能较好地衡量现有模型是否有很好描述的线性趋势。
(2)平均百分比误差(Mean Percentage Error, MPE):
M
P
E
=
1
T
2
∑
t
=
T
1
+
1
T
1
+
T
2
e
t
y
t
MPE=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}\frac{e_t}{y_t}
MPE=T21t=T1+1∑T1+T2ytet平均百分比误差也用于衡量是否有短期趋势没有被模型很好地描述,不过它是以相对误差的形式来表达的。
(3)均方差(Mean Square Error, MSE):
M
S
E
=
1
T
2
∑
t
=
T
1
+
1
T
1
+
T
2
e
t
2
MSE=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}e_t^2
MSE=T21t=T1+1∑T1+T2et2均方差能侦测出线性趋势之外更多的没有被模型描述的数据模式,比如周期性等,因此更为常用。
(4)平均绝对误差(Mean Absolute Error, MAE):
M
A
E
=
1
T
2
∑
t
=
T
1
+
1
T
1
+
T
2
∣
∣
e
t
∣
∣
MAE=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}||e_t||
MAE=T21t=T1+1∑T1+T2∣∣et∣∣平均绝对误差在衡量模型的准确度方面和均方差有类似的效果,只是对于异常值相对来说稳健性更高。
(5)平均绝对百分比误差(Mean Absolute Percentage Error, MAPE):
M
A
P
E
=
1
T
2
∑
t
=
T
1
+
1
T
1
+
T
2
∣
∣
e
t
y
t
∣
∣
MAPE=\frac{1}{T_2}\sum_{t=T_1+1}^{T_1+T_2}||\frac{e_t}{y_t}||
MAPE=T21t=T1+1∑T1+T2∣∣ytet∣∣MAPE结合了MAE和MPE的优点,能较好地侦测线性趋势之外的更多的数据模式,并以相对误差的形式表达。
使用样本外数据验证步骤
(1)将长度为
T
=
T
1
+
T
2
T=T_1+T_2
T=T1+T2的样本时间序列分为两个子序列,其中前面一个
(
t
=
1
,
.
.
.
,
T
1
)
(t=1,...,T_1)
(t=1,...,T1)子序列用于模型训练,后面一个子序列
(
t
=
T
1
+
1
,
.
.
.
,
T
)
(t=T_1+1,...,T)
(t=T1+1,...,T)用于模型验证。
(2)用第一个子序列训练一个待验证模型。
(3)使用上一步训练的模型,使用时间范围为
t
=
1
,
.
.
.
,
T
1
t=1,...,T_1
t=1,...,T1的因变量来预测未来
T
1
+
1
,
.
.
.
,
T
T_1+1,...,T
T1+1,...,T时间段的因变量值:
y
^
t
\hat{y}_t
y^t,即对用于模型验证部分的子序列因变量使用待验证模型进行拟合。
(4)使用上一步拟合的因变量值和对应的实际因变量值,计算单步预测误差:
e
t
=
y
t
−
y
^
t
e_t=y_t-\hat{y}_t
et=yt−y^t,然后采用一种或者多种上面介绍的衡量模型准确度的统计量来计算综合预测能力。
可以对每一个待验证模型都执行第(2)到第(4)步,选取综合预测能力最好,即统计量值最小的那个待选模型。
时间序列数据示例
单变量时间序列数据集
以下是4个单变量时间序列数据集,包含销售、气象学、物理学和人口学等一系列领域的这些数据集。
- 洗发水销售数据集
- 每日最低温度数据集
- 每月太阳黑子数据集
- 每日女性出生数据集
多元时间序列数据集
多元时间序列数据的一个重要来源是UCI 机器学习存储库:https://archive.ics.uci.edu/ml/index.php
- 脑电眼状态数据集
- 占用检测数据集
- 臭氧水平检测数据集
简要回顾ARIMA时间序列模型
ARIMA模型即自回归积分移动平均(Auto Regression Integrated Moving Average)模型,ARIMA模型通常写作ARIMA(p,d,q),其中:
(1)p指自回归项的个数,是使用取差分平稳化以后的新时间序列的过去值作为解释变量部分的个数。
(2)d指将序列平稳化所需的差分次数,反过来,从平稳化的序列变化为原始数据的算法即称为预测方程。假如原始数据为
Y
t
Y_t
Yt,而差分后的平稳数据为
y
t
y_t
yt,如果
d
=
0
d=0
d=0,则
Y
t
=
y
t
Y_t=y_t
Yt=yt,如果
d
=
1
d=1
d=1,则
Y
t
=
y
t
+
Y
t
−
1
Y_t=y_t+Y_{t-1}
Yt=yt+Yt−1,而如果
d
=
2
d=2
d=2,则
Y
t
=
(
y
t
+
Y
t
−
1
)
+
(
Y
t
−
1
−
Y
t
−
2
)
Y_t=(y_t+Y_{t-1})+(Y_{t-1}-Y_{t-2})
Yt=(yt+Yt−1)+(Yt−1−Yt−2)。
(3)q对应移动平均部分,指预测方程里预测误差的滞后项个数。
这是一类非常灵活的时间序列预测模型,通常使用在可以通过差分变换为平稳序列的时间序列数据上。注意,在对时间序列数据进行平稳化的过程中,通常也一起使用对数或者Box-Cox变换等手段。(弱)平稳序列的含义是指这个数据没有特定的趋势,并且其围绕其平均值按照比较一致的波幅进行波动。这个波幅一致的波动意味着其自相关系数不随时间而变化,或者说其功率频谱不变。这种事件序列数据可以被看成一个信号和一个噪声项的组合,其信号项部分可以是一个或者多个往复的三角函数曲线以及其他周期性信号的组合。从这个角度看,ARIMA模型可以看作一个试图将信号与噪声分离的滤子,并使用外推法预测未来值。
ARIMA模型的一般形式写作:
y
^
t
=
μ
+
α
y
t
−
1
+
.
.
.
+
α
p
y
t
−
p
+
β
1
e
t
−
1
−
.
.
.
−
β
q
e
t
−
q
\hat{y}_t=\mu+\alpha y_{t-1}+...+\alpha_p y_{t-p}+\beta_1 e_{t-1}-...-\beta_q e_{t-q}
y^t=μ+αyt−1+...+αpyt−p+β1et−1−...−βqet−q
使用ARIMA模型建模的步骤如下:
(1)可视化待建模的序列数据。
(2)使用ADF或者KPSS测试确定将数据平稳化所需的差分次数。
(3)使用ACF/PACF确定移动平均对应的预测误差项和自回归项个数,一般从一项开始。
(4)对于拟合好的ARIMA模型,将预测误差项和自回归项分别减少一个再拟合。
(5)根据AIC或者BIC判断模型相对简单的AR或者MA模型是否有改进。
(6)对自回归和移动平均项个数递增一个,逐次检验。
对于自相关项,一般可以通过增加自回归项或者移动平均部分里面的预测误差项个数来消除。一般的原则是如果未消除的自相关是正自相关关系,即ACF图里面第一项是正值,则使用增加自回归项的方法较好;而如果未消除的自相关是负自相关关系,则增加预测误差项的方法会更为合适。这是因为一般而言,差分方法对于消除正相关关系非常有效,但是同时也会额外引入反向的相关关系,这时候会出现过度差分的情况,需要额外引入一个预测误差项来消除负相关关系,这也是为什么在上面的建模步骤里面先引入预测误差项建模,而不是先引入自回归项开始建模,也就是先拟合一个ARIMA(0,1,1)模型再看看ARIMA(1,1,0)模型,通常ARIMA(0,1,1)模型会比ARIMA(1,1,0)模型拟合效果好一些。
识别差分项的原则
(1)如果建模的序列正的自相关系数一直衍生到很长的滞后项(比如10或者更多滞后项),则获得平稳序列所需的差分次数较多。
(2)如果滞后一项的自相关系数为0或者为负,或者所有的自相关系数都很小,则该序列不需要更多的差分来获得平稳性。通常而言,如果之后一项的自相关性为-0.5或者更小,则很可能该序列被过度差分了,这是需要注意的。
(3)最优的差分项个数通常对应于差分后拥有最小标准差的时间序列。
(4)如果原序列不需要进行差分,则假定原序列是平稳的。一阶差分则意味着原序列有一个为常数的平均趋势。二阶差分则意味着原序列有一个依时间变化的趋势。
(5)对不需要进行差分的时间序列建模时通常包含一个常数项。如果对一个需要一阶差分的时间序列进行建模,则只有在该时间序列包含非0的平均趋势的时候才需要包含常数项。而对一个需要进行二阶差分的时间序列进行建模时则通常不用包含常数项。
识别自回归或者预测误差项的原则
(1)如果差分后的序列是PACF显示为Sharp Cutoff或者滞后一项的自相关为正,则说明该序列差分不足,这时候可以对模型增加一个或者多个自相关项,增加个数通常为PACF Cutoff的地方。
(2)如果差分后的序列的ACF显示为急剧截断或者滞后一项的自相关为负相关,则说明该序列差分过度,这时候可以对模型增加一个或者多个预测误差项,增加个数通常为ACF截断(Cutoff)的地方。
(3)自回归项和预测误差项有可能会互相抵消,因此如果一个两种要素都包含的ARIMA模型对数据拟合得很好,则通常可以试一试一个少一个自回归项或者少一预测误差项的模型。一般来说,同时包含多个自回归和多个预测误差项的ARIMA模型都会过度拟合。
(4)如果自回归项的系数和接近1,即自回归部分有单位根现象,那么这个时候应该将自回归项减少一个,同时增加一次差分操作。
(5)如果预测误差项的系数和接近1,即移动平均部分有单位根现象,那么这时候应该将预测误差项减少一个,同时减少一次差分操作。
(6)自回归或者移动平均部分有单位根通常也表现为长期预测不稳定。
识别模型的季节性
(1)如果一个时间序列有很强的季节性,则必须使用一次季节周期作为差分,否则模型会认为季节性会随着时间逐渐消失。但是使用季节周期做差分不能超过一次,如果使用了季节周期做差分,则非季节周期的差分最多也只能再进行一次。
(2)如果一个适当差分之后的序列的自相关系数在第s个滞后上仍然表现为正,而s为季节性周期包含的时间段数,则在模型里添加一个季节性自回归项。如果这个自相关系数为负,则添加一个季节性预测误差项。通常情况下,如果已经使用了季节周期做差分,则第二种情况更常见,而第一种情况通常是还没有使用季节性周期做差分。如果季节性周期很规律,则使用差分是比引入一个季节性自回归项更好的方法。应尽量避免在模型里同时引入季节性自回归和季节性预测误差项,否则模型会过拟合,甚至在拟合过程本身会出现不收敛的情况。
循环神经网络与时间序列模型
循环神经网络主要用于处理和预测序列数据。循环神经网络存在较少参数,其中时序信息以及语义信息的深度表达能力被充分利用,并在语音识别、语言模型、机器翻译以及时序分析等方面实现了突破。
一个典型的循环神经网络基本结构如下:
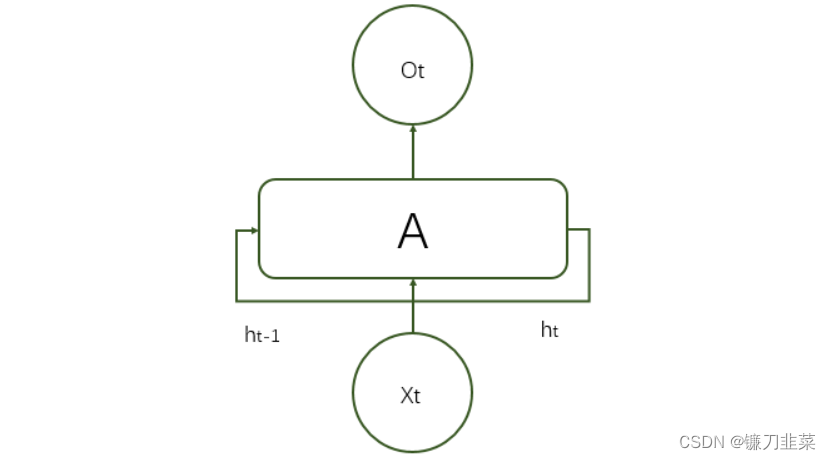
在每一个时刻
t
t
t,循环神经网络会针对该时刻的输入结合当前模型的状态给出一个输出,并更新模型状态。如图所示,循环神经网络的主体结构
A
A
A输入层除了来自输入层
X
t
X_t
Xt外,还提供上一时刻的隐藏状态
h
t
−
1
h_{t-1}
ht−1 。类似于卷积神经网络在不同空间共享参数,循环神经网络在不同时间共享参数,从而能够使用有限的参数处理任意长度的序列。
将完整的输入输出序列展开:
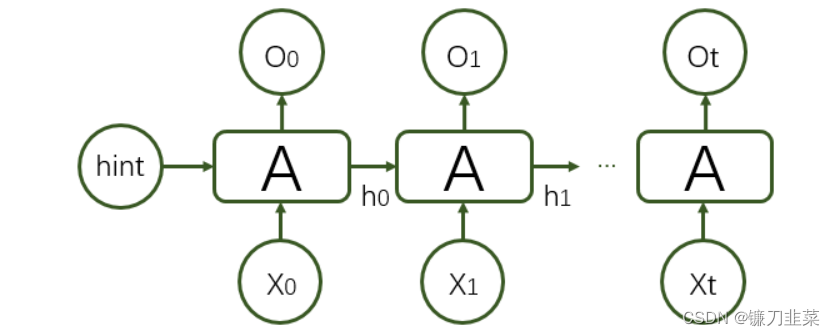
循环网络的展开在模型训练中有重要意义。如上图所示,也就是在时间上展开后的循环神经网络结构。对长度为N的RNN展开后,就类似于CNN中间层的结构,只不过RNN的中间层是在时间层面上展开的。RNN上使用反向传播被称为”沿时间反向传播(Back-Propagation Through Time)”,是训练RNN的最常用方法。
从结构上来看,RNN擅长解决与时间序列相关的问题。对于一个序列数据,可以将不同时刻的数据依次传入循环神经网络的输入层,而输出是下一个时刻的预测,或者是对当前时刻信息的处理结果(比如语音识别结果)。
循环神经网络可以看作是同一神经网络结构在时间序列上被复制多次的结果,这个被复制多次的结构被称为循环体。循环神经网络中的状态是通过一个向量来表示的,这个向量的维度也称为循环神经网络隐藏层的大小,假设其为
n
n
n。如下图所示,循环体的输入有两部分,一部分为上一时刻的状态,另一部分为当前时刻的输入样本。对于时间序列数据来说(比如不同时刻商品的销售),每一时刻的输入样例可以是当前时刻的数值(比如销售量);对于语言模型来说,输入样例可以是当前单词对应的单词向量(word embedding)。
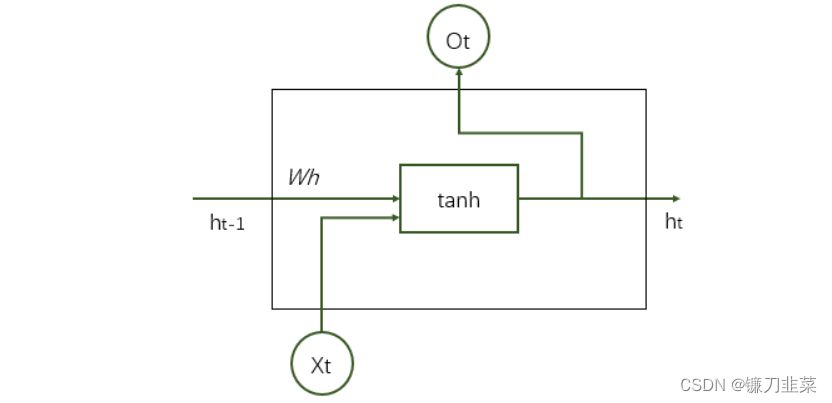
下图展示了一个循环神经网络前向传播的具体计算过程:
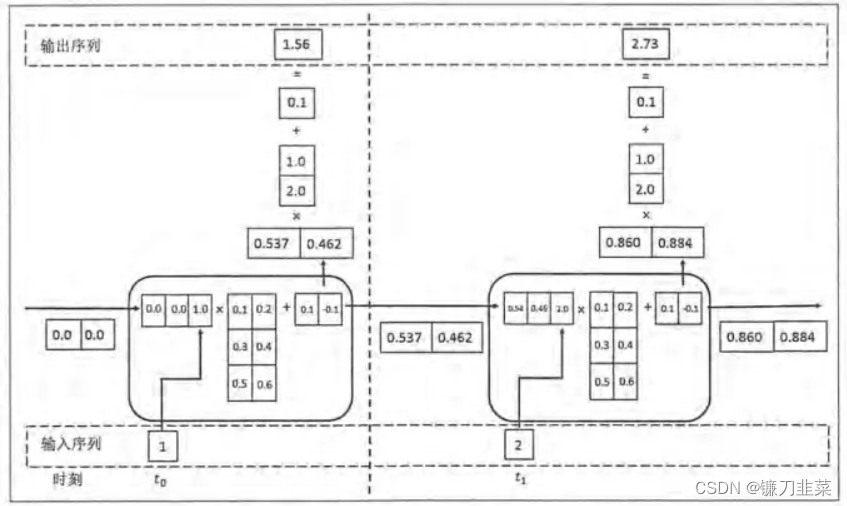
示例代码:
import numpy as np
# 定义RNN参数
X = [1, 2]
state = [0.0, 0.0]
# 分开定义不同输入部分的权重以方便操作
w_cell_state = np.asarray([[0.1,0.2],[0.3,0.4]])
w_cell_input = np.asarray([0.5,0.6])
b_cell = np.asarray([0.1,-0.1])
# 定义用于输出的全连接层参数
w_output = np.asarray([[1.0],[2.0]])
b_output = 0.1
# 执行前向传播过程
for i in range(len(X)):
# 计算循环体中的全连接层神经网络
before_activation = np.dot(state, w_cell_state)+X[i]*w_cell_input+b_cell
state = np.tanh(before_activation)
# 根据当前时刻状态计算最终输出
final_output = np.dot(state, w_output)+b_output
# 输出每个时刻的信息:
print('before activation:', before_activation)
print('state:',state)
print('output:',final_output)
'''
before activation: [0.6 0.5]
state: [0.53704957 0.46211716]
output: [1.56128388]
before activation: [1.2923401 1.39225678]
state: [0.85973818 0.88366641]
output: [2.72707101]
'''
注意:在实际训练中,如果序列过长,一方面会导致优化时出现梯度消失和梯度爆炸问题,另一方面,展开后的前馈神经网络会占用过大的内存,所以实际上一般会规定一个最大长度,当序列长度超过规定长度滞后会对序列进行截断。
长短时记忆网络(LSTM)
目的是为了解决复杂语言场景中相关信息间隔大小不一致的问题。作为一种特殊的循环体结构,LSTM由三个门结构构成:
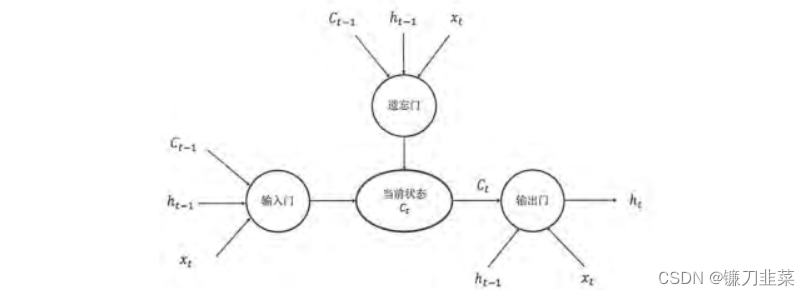
门的结构由一个使用sigmoid神经网络和一个按位乘法操作构成。sigmoid通过0,1设置,表示信息是否通过。
在这几种门中:输入门和遗忘门非常重要。
遗忘门:让RNN”忘记“之前没有用的信息。假设状态c的维度为n,”遗忘门“会根据当前的输入
x
t
x_t
xt和上一时刻输出
h
t
−
1
h_{t-1}
ht−1计算一个维度为n的向量
f
=
s
i
g
m
o
i
d
(
W
1
x
+
W
2
h
)
f=sigmoid(W_1x+W_2h)
f=sigmoid(W1x+W2h),它在每一维度上的值都在(0,1)范围内。再将上一时刻的状态
c
t
−
1
c_{t-1}
ct−1与
f
f
f向量按位相乘,那么
f
f
f取值接近0的维度上的信息就会被”遗忘“,而
f
f
f取值接近1的维度上的信息会被保留。
输入门:根据
x
t
x_t
xt和
h
t
−
1
h_{t-1}
ht−1决定哪些信息加入到状态
c
t
−
l
c_{t-l}
ct−l中生成新的状态
c
t
c_t
ct。
输出门:根据最新的状态
c
t
c_t
ct、上一时刻的输出
h
t
−
1
h_{t-1}
ht−1和当前的输入
x
t
x_t
xt来决定该时刻的输出
h
t
h_t
ht。
下面是LSTM的细胞(Cell),每个细胞可视作4层:
遗忘层(Forget layer):
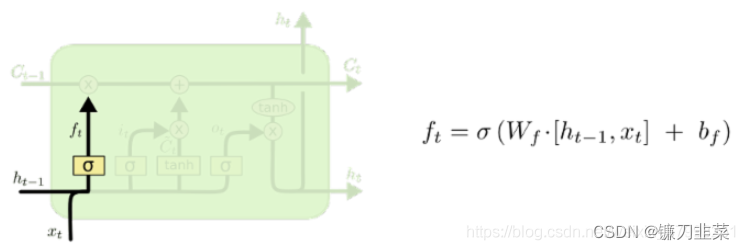
确定更新的信息:
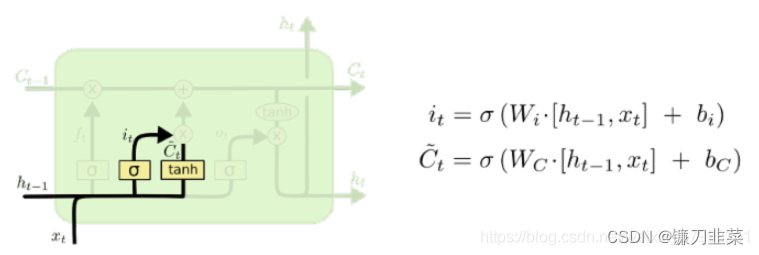
更新细胞的状态:
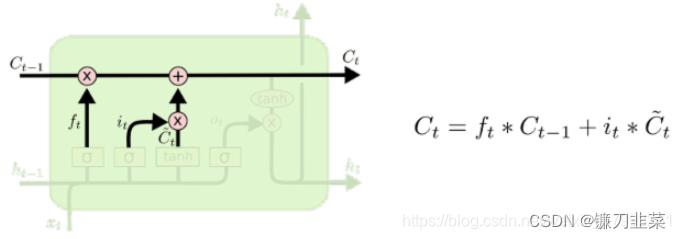
输出信息:
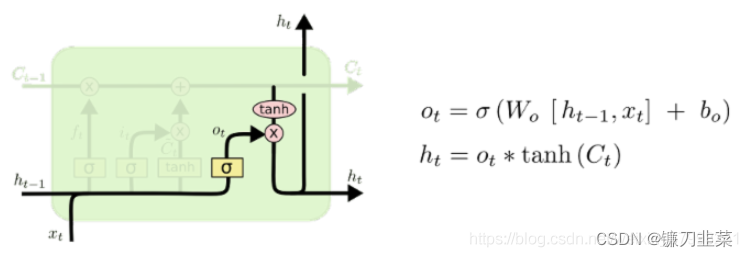
综合来看:
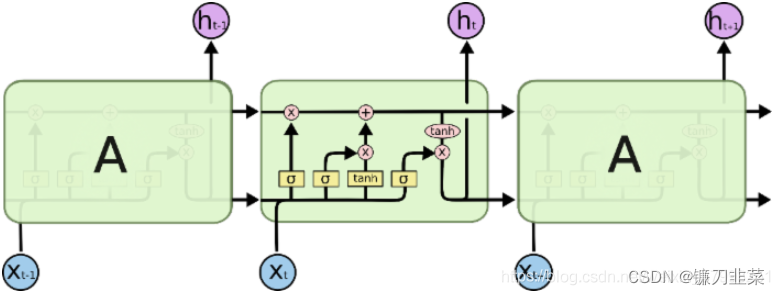
具体LSTM每个”门“的公式定义如下:
- 输入值: z = t a n h ( W z [ h t − 1 , x t ] ) z=tanh(W_z[h_{t-1},x_t]) z=tanh(Wz[ht−1,xt])
- 输入门: i = s i g m o i d ( W i [ h t − 1 , x t ] ) i = sigmoid(W_i[h_{t-1},x_t]) i=sigmoid(Wi[ht−1,xt])
- 遗忘门: f = s i g m o i d ( W f [ h t − 1 , x t ] ) f=sigmoid(W_f[h_{t-1},x_t]) f=sigmoid(Wf[ht−1,xt])
- 输出门: o = s i g m o i d ( W o [ h t − 1 , x t ] ) o = sigmoid(W_o[h_{t-1},x_t]) o=sigmoid(Wo[ht−1,xt])
- 新状态: c t = f ⋅ c t − 1 + i ⋅ z c_t=f\cdot c_{t-1}+i\cdot z ct=f⋅ct−1+i⋅z
- 输出: h t = o ⋅ tanh c t h_t=o\cdot \text{ tanh } c_t ht=o⋅ tanh ct
其中
W
z
,
W
i
,
W
f
,
W
o
W_z, W_i, W_f, W_o
Wz,Wi,Wf,Wo是4个维度为[2n,n]的参数矩阵,用流程图的形式表示上面的公式:
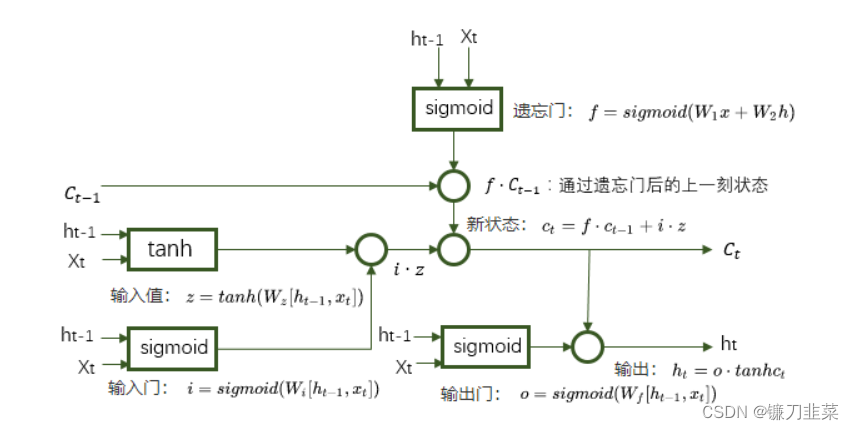
使用Tensorflow实现使用LSTM结构的RNN前向传播过程:
'''
基于Tensorflow V1版本的代码
'''
# 定义一个LSTm结构
# LSTM中使用的变量也会在该函数中被自动声明
lstm = tf.nn.rnn_cell.BasicLSTMCell(lstm_hedden_size)
# 将LSTM状态初始化为0的数组
# zero_state函数生成全0的初始状态;state.c和state.h分贝代表c和h状态
state = lstm.zero_state(batch_size, tf.float32)
# 定义损失函数
loss = 0.0
# 训练中为了将循环网络展开成前馈神经网络,我们需要知道数据序列长度
# num_steps表示长度
for i in range(num_steps):
# 第一个时刻声明LSTm结构中使用的变量,之后都需要复用之前定义好的变量
if i > 0:
tf.get_variable_scope().reuse_variables()
# 每一步处理时间序列中的一个时刻
lstm_output, state = lstm(current-input, state)
# 当前时刻的LSTM结构的输出传入一个全连接层得到最后的输出
final_output = fully_connected(lstm_output)
# 计算当前时刻输出的损失
loss += calc_loss(final_output, expected_output)
LSTM变种:GRU
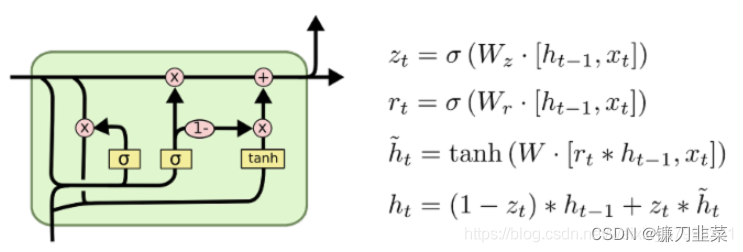
循环神经网络的变种
双向循环神经网络和深层循环神经网络
双向循环神经网络
单个单词前后句子都会对单词的识别有影响,所以有了双向循环神经网络。双向循环神经网络是由两个独立的循环神经网络叠加在一起的,输出由两个循环神经网络的输出拼接而成。因为当前时刻的输出不仅和之前的状态有关,也和之后的状态有关。这时就需要根据前文来判断,同时需要后面的内容。例子就像选择填空一样需要前后度进行分析。示例如下:
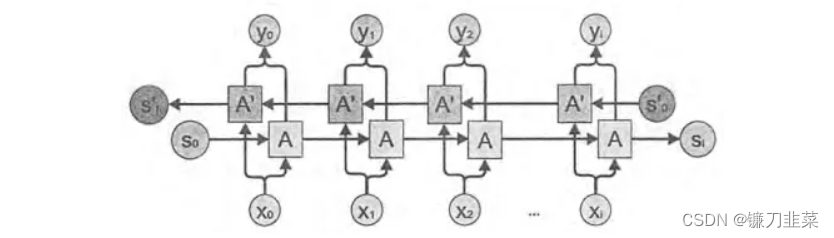
深层循环神经网络
深层循环神经网络(Deep RNN)为了增强模型的表达能力而网络中设置了多个循环层。每一时刻的输入
x
t
x_t
xt到输出
o
t
o_t
ot之间有
L
L
L个循环体。网络因此可以从输入中抽取更加高层的信息。和CNN类似,每一层的循环体中参数是一致的,而不同层中的参数可以不同。TensorFlow中提供了MultiRNNCell类实现深层循环神经网络的传播过程。
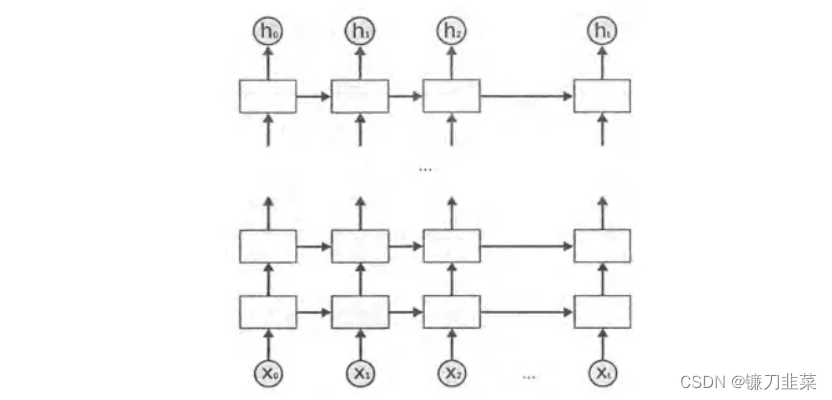
循环神经网络的dropout
通过dropout,可让网络更加健壮,只在最后的全连接层中使用dropout。而在同一时刻 t t t中,不同层循环体之间会使用dropout。在Tensorflow中,使用tf.nn.rnn_cell.DropoutWrapper类可以实现dropout功能。
时间序列数据建模实战
本文利用TensorFlow2.0建立时间序列RNN模型,对国内的新冠肺炎疫情结束时间进行预测。
数据准备
本文的数据集取自tushare。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import models, layers, losses, metrics, callbacks
数据预览:
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
df = pd.read_csv('../DemoData/covid-19.csv', sep='\t')
df.plot(x='date', y=['confirmed_num','cured_num','dead_num'], figsize=(10, 5))
plt.xticks(rotation=60)
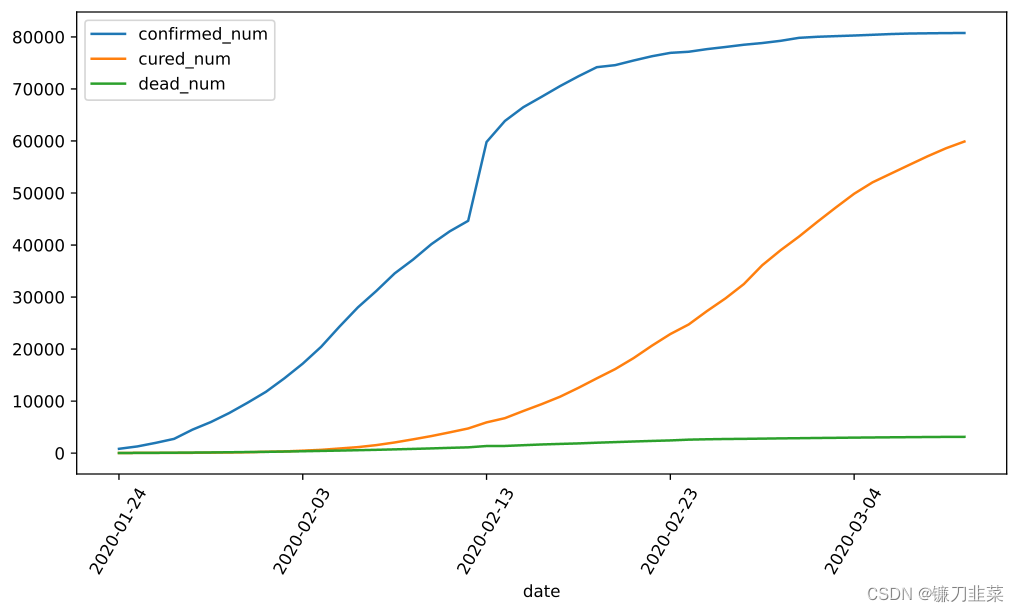
dfdata = df.set_index('date')
dfdiff = dfdata.diff(periods=1).dropna()
dfdiff = dfdiff.reset_index('date')
dfdiff.plot(x='date', y=["confirmed_num","cured_num","dead_num"], figsize=(10, 5))
plt.xticks(rotation=60)
dfdiff = dfdiff.drop('date', axis=1).astype('float32')
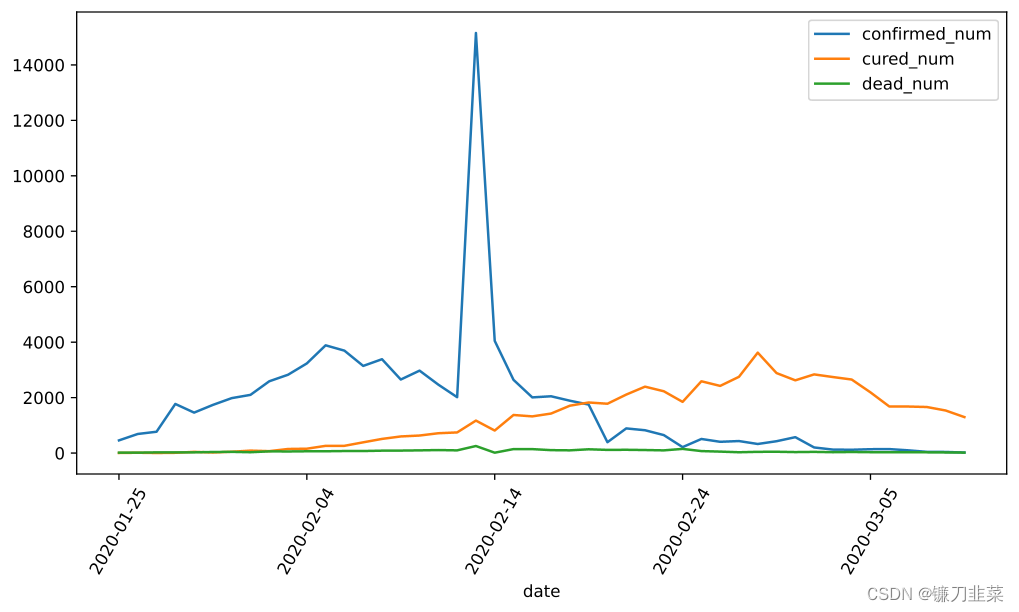
用某日前8天窗口数据作为输入预测该日数据:
WINDOW_SIZE = 8
def batch_dataset(dataset):
dataset_batched = dataset.batch(WINDOW_SIZE, drop_remainder=True)
return dataset_batched
ds_data = tf.data.Dataset.from_tensor_slices(tf.constant(dfdiff.values, dtype=tf.float32)).window(WINDOW_SIZE, shift=1).flat_map(batch_dataset)
ds_label = tf.data.Dataset.from_tensor_slices(tf.constant(dfdiff.values[WINDOW_SIZE:],dtype=tf.float32))
# 数据较小,将全部训练数据放入到一个batch中
ds_train = tf.data.Dataset.zip((ds_data, ds_label)).batch(38).cache()
定义模型
使用Keras接口有以下3种方式构建模型:
- 使用Sequential按层顺序构建模型,
- 使用函数式API构建任意结构模型,
- 继承Model基类构建自定义模型
这里选择函数式API构建任意结构模型:
# 考虑到新增确诊,新增治愈、新增死亡人数数据不可能小于0,设计如下结构
class Block(layers.Layer):
def __init__(self, **kwargs):
super(Block, self).__init__(**kwargs)
def call(self, x_input, x):
x_out = tf.maximum((1+x)*x_input[:,-1,:], 0.0)
return x_out
def get_config(self):
config = super(Block, self).get_config()
return config
定义模型:
tf.keras.backend.clear_session()
x_input = layers.Input(shape=(None, 3), dtype=tf.float32)
x = layers.LSTM(3, return_sequences=True, input_shape=(None, 3))(x_input)
x = layers.LSTM(3, return_sequences=True, input_shape=(None, 3))(x)
x = layers.LSTM(3, return_sequences=True, input_shape=(None, 3))(x)
x = layers.LSTM(3, input_shape=(None, 3))(x)
x = layers.Dense(3)(x)
x = Block()(x_input, x)
model = models.Model(inputs=[x_input], outputs = [x])
model.summary()
'''
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, None, 3)] 0 []
lstm (LSTM) (None, None, 3) 84 ['input_1[0][0]']
lstm_1 (LSTM) (None, None, 3) 84 ['lstm[0][0]']
lstm_2 (LSTM) (None, None, 3) 84 ['lstm_1[0][0]']
lstm_3 (LSTM) (None, 3) 84 ['lstm_2[0][0]']
dense (Dense) (None, 3) 12 ['lstm_3[0][0]']
block (Block) (None, 3) 0 ['input_1[0][0]',
'dense[0][0]']
==================================================================================================
Total params: 348
Trainable params: 348
Non-trainable params: 0
__________________________________________________________________________________________________
'''
训练模型
训练模型通常有3种方法,内置fit方法,内置train_on_batch方法,以及自定义训练循环。这里选择最常用也最简单的内置fit方法。
需要注意的是,RNN调试比较困难,需要设置多个不同的学习率多次尝试,以便取得最好的效果。
# 自定义损失函数,考虑平方差和预测目标的比值
class MSPE(losses.Loss):
def call(self, y_true, y_pred):
err_precent = (y_true-y_pred)**2/(tf.maximum(y_true**2, 1e-7))
mean_err_precent = tf.reduce_mean(err_precent)
return mean_err_precent
def get_config(self):
config = super(MSPE, self).get_config()
return config
import os
import datetime
from pathlib import Path
optimizer = tf.keras.optimizers.Adam(learning_rate=0.01)
model.compile(optimizer=optimizer, loss=MSPE(name='MSPE'))
stamp = datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
logdir = str(Path('../DemoData/autograph/' + stamp))
tb_callback = tf.keras.callbacks.TensorBoard(logdir, histogram_freq=1)
# 如果loss在100个epoch后没有提升,学习率减半
lr_callback = tf.keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=100)
# 当loss在200个epoch后没有提升,则提前终止训练
stop_callback = tf.keras.callbacks.EarlyStopping(monitor='loss', patience=200)
callbacks_list = [tb_callback, lr_callback, stop_callback]
history = model.fit(ds_train, epochs=500, callbacks=callbacks_list)
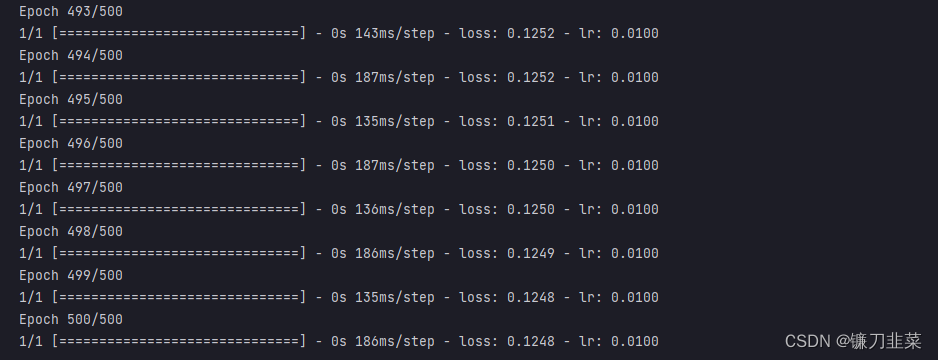
评估模型
评估模型一般要设置验证集或者测试集,由于此例数据较少,仅仅可视化损失函数在训练集上的迭代情况。
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
def plot_metric(history, metric):
train_metrics = history.history[metric]
epochs = range(1, len(train_metrics)+1)
plt.plot(epochs, train_metrics, 'bo--')
plt.title('Training'+metric)
plt.xlabel('Epochs')
plt.ylabel(metric)
plt.legend(['train_'+metric])
plt.show()
查看损失变化情况:
plot_metric(history, 'loss')
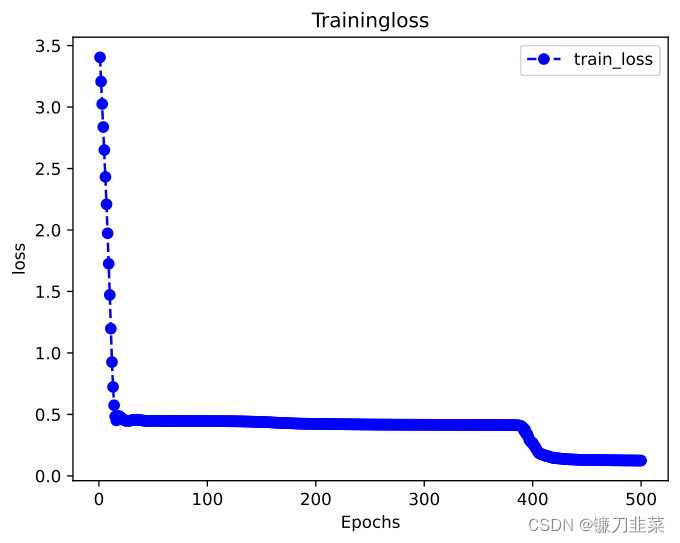
使用模型
此处使用模型预测疫情结束时间,即新增确诊病例为0的时间。
使用dfresult记录现有数据以及此后预测的疫情数据:
dfresult = dfdiff[["confirmed_num","cured_num","dead_num"]].copy()
dfresult.tail()
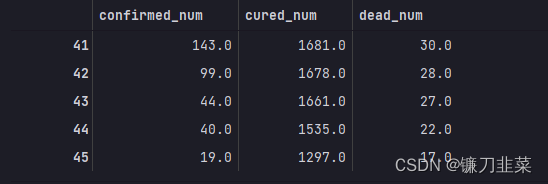
预测此后100天的新增走势,将其结果添加到dfresult中:
for i in range(100):
arr_predict = model.predict(tf.constant(tf.expand_dims(dfresult.values[-38:,:], axis=0)))
dfpredict = pd.DataFrame(tf.cast(tf.floor(arr_predict),tf.float32).numpy(), columns=dfresult.columns)
dfresult = dfresult.append(dfpredict, ignore_index=True)
# 查看新增确诊数降为0的日期
dfresult.query('confirmed_num==0').head()
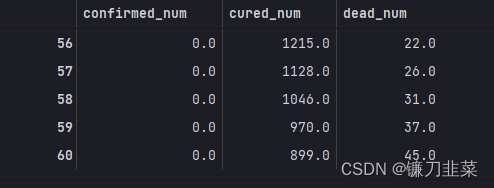
第56天开始新增确诊降为0,第45天对应3月10日,也就是11天后,即预计3月21日新增确诊降为0。(显然过于乐观)
查询新增治愈数为0的日期:
for i in range(100):
arr_predict = model.predict(tf.constant(tf.expand_dims(dfresult.values[-38:,:], axis=0)))
dfpredict = pd.DataFrame(tf.cast(tf.floor(arr_predict),tf.float32).numpy(), columns=dfresult.columns)
dfresult = dfresult.append(dfpredict, ignore_index=True)
dfresult.query("cured_num==0").head()
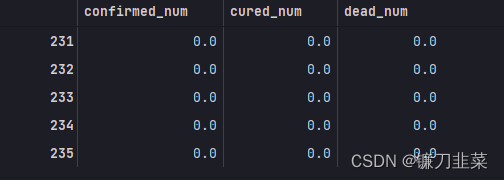
第231天开始新增治愈降为0,第45天对应3月10日,也就是大概6个月后,即9月16日左右全部治愈。
查询新增死亡降为0的日期:
for i in range(100):
arr_predict = model.predict(tf.constant(tf.expand_dims(dfresult.values[-38:,:], axis=0)))
dfpredict = pd.DataFrame(tf.cast(tf.floor(arr_predict),tf.float32).numpy(), columns=dfresult.columns)
dfresult = dfresult.append(dfpredict, ignore_index=True)
dfresult.query("dead_num==0").head()
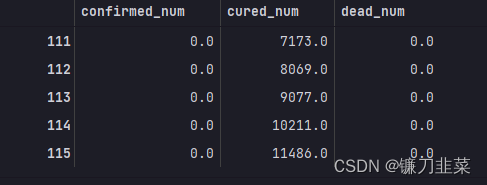
第111天开始,新增死亡降为0,第45天对应3月10日,也就是5月16日后,新增死亡降为0
保存模型
使用TensorFlow原生方式保存模型:
model.save('../../data/tf_model_savedmodel', save_format="tf")
print('export saved model.')
模型加载和使用:
model_loaded = tf.keras.models.load_model('../../data/tf_model_savedmodel',compile=False)
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
model_loaded.compile(optimizer=optimizer,loss=MSPE(name = "MSPE"))
model_loaded.predict(ds_train)
参考资料
[1] 《Keras快速上手:基于Python的深度学习实战》
[2] 7个常用的时间序列数据集
[3] 《Tensorflow:实战Google深度学习框架》
[4] 30天吃掉那只Tensorflow2