一.数据类型分类

二.整形的存储形式

1.源码，反码，补码的关系

内存中数据的存储——二进制

  在（signed）int类型中大小为4个字节，1个字节是8个比特位，一个比特位是存数据的最小内存单元，也就是二进制的0/1，那四个字节就是32位二进制的数，并且最高位是符号位（因为是signed）。

源码，反码，补码的关系

正数

说明：源码，反码，补码相同。
举例1：

int a =1;

源码：00000000000000000000000000000001
反码：00000000000000000000000000000001
补码：00000000000000000000000000000001（在内存中实际存的数据）
注意：计算机并不是直接把正数的源码存进去了，而是把源码转换为补码存进去了。

负数

说明：遵循着运算逻辑——反码等于源码按位取反（符号位，也就是最高位不变，把源码中的0变成1，1变成0），补码等于反码加上1。
图解：

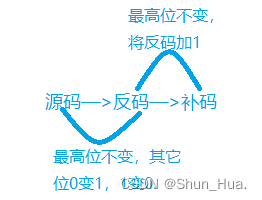
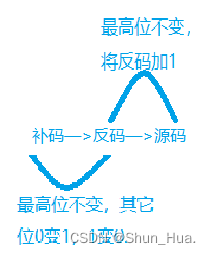
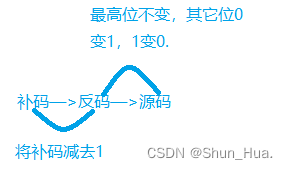
特殊：int的取值范围：-2147483648 ~2147483647
负数的最小值的存储为：10000000000000000000000000000000（这是补码，并且这是语法规定的）
因此我们可以这样记住负数与正数的存储形式：

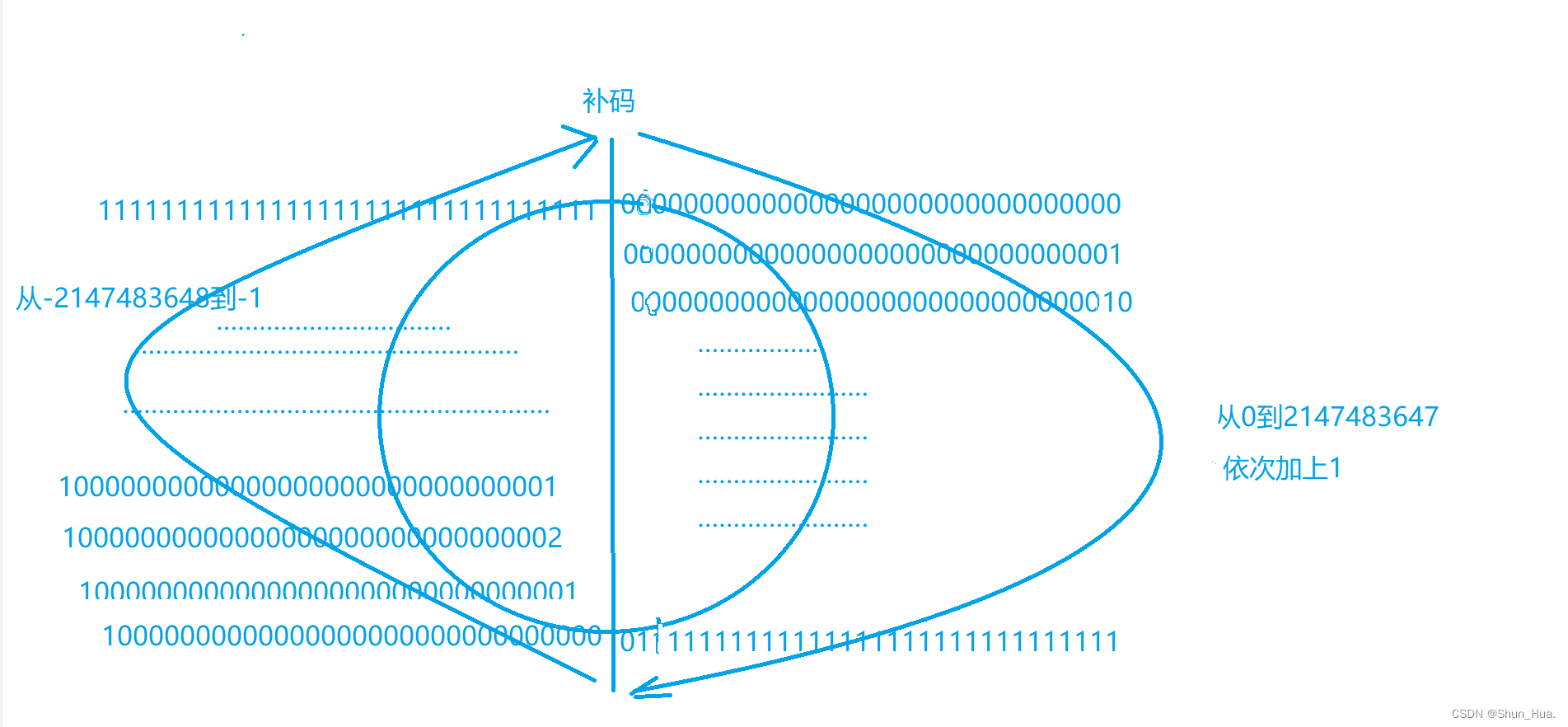
我们可以看出,这是一个轮回,是不是很神奇？

举例2：

int a =-1;

源码：10000000000000000000000000000001
反码：1111111111111111111111111111111111110
补码：1111111111111111111111111111111111111
在内存中：

说明：二进制1111表示一个f（十六进制）

三.大小端

1.概念

int main()
{
	int a = 0x11223344;
	return 0;
}

内存：

为什么不是：11 22 33 44呢？
这里要引出大小端的问题：
大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位保存在内存的低地址
中；
小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位保存在内存的高地址中
简单来说：大异小同。

那么这里的存储形式就为小端存储。

2.例题：判断当前编译器的存储形式

void test()
{
	int i = 1;//内存（小端存储）里面放的是：01 00 00 00
	char* p = (char*)&i;
	if (*p == 1)
	{
		printf("小端存储\n");
	}
	else
	{
		printf("大端存储\n");
	}
}
int main()
{
	test();
	return 0;
}

四.浮点数的存储形式

1.二进制的补充：

小数位：
0.1（二进制）表示的是12的-1次方
0.01表示的是 12的-2次方
举例：
0.3（十进制）转化为2进制。
小数点后计算:
取整数位
0.32=0.6----0
0.62=1.2----1
0.22=0.4----0
0.42=0.8----0
0.82=1.6----1
0.62=1.2----1 //开始循环
…
1001就是循环节
其它的类似。

2.存储标准

 根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：
(-1)^S * M * 2^E
1.(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
2.M表示有效数字，大于等于1，小于2。
3.2^E表示指数位。
举例：

float =9.0f;

9
转化为二进制为：00000000 00000000 00000000 00001001
转化为小数：1.0012的三次方
因为是正数，可以表示为（-1）的0次方 * 1.0012的三次方
那么：这里的S为0，M为1.001，E为3
说明：float的大小为4个字节：32比特位。
IEEE 754规定：
对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。

这里的内存分配就是这样的。
说明：E为无符号的类型，为了存正数和负数，则规定要加上一个127。
那么这里的E为3+127=130.转换为二进制：10000010
M规定1整数忽略，在取出的时候，默认加1，这样可以多1位精度。
这里存入的M为：001其它位置默认补0
因此9.0的存储形式为：0 10000010 00100000000000000000000
转化为16进制：41 10 00 00
小端存储：00 00 10 41
补充：
1.E全为0：
这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。
2.E全为1：
这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；
例题：从float和int视角观察9.0

int main()
{
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	*pFloat = 9.0;
	printf("num的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

结果：

解析：从flaot的视角观察 int类型的9.0
补码：00000000 00000000 00000000 00001001
分为三部分：0 00000000 00000000000000000001001
S:0——符号是+
E:0—— 则为1-127=-126
M:1.00000000000000000001001
写成科学计数法的形式：1.00000000000000000001001*2的-126次方——这是一个很小的数字，几乎为0。
从int类型视角观看float类型的9.0
补码：0 10000010 00100000000000000000000
int类型的补码：01000001000100000000000000000000
源码：01000001000100000000000000000000
转化为十进制：1091567616

double跟float差不多，不过分配的储存数值空间有所不同而已。