[LC 总结] 前缀和(Prefix Sum)总结& 10 道相关练习题
类型与题目列表如下:
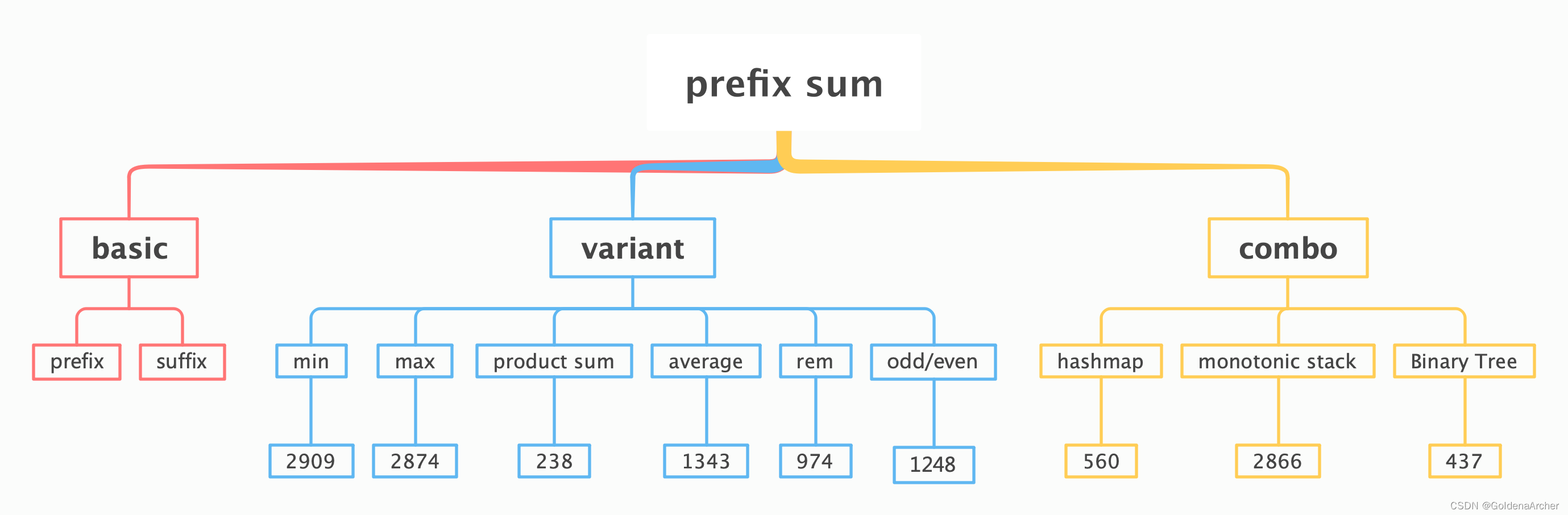
题目的解法都做过了,会留在最后一个部分,接下来就梳理一下 prefix sum,列举的题目从简单到 -> 困难
基础
prefix sum 其本身是一个数组相关的数据类型,它的实现方法也非常的简单,以存在数组 nums 为例,就是使用另外一个数组,保存
∑
k
=
i
i
n
u
m
s
[
k
]
\sum_{k=i}^{i} nums[k]
∑k=iinums[k] 的值,以 [1, 2, 3, 4, 5] 为例,对应的 prefix sum 为 [1, 3, 6, 10, 15] 或 [0, 1, 3, 6, 10, 15]
prefix sum 的走向为 0 -> len(nums),如果是走向为 len(nums) -> 0,那么这个被称之为 suffix sum,或是 postfix sum,以 [1, 2, 3, 4, 5] 来说,它所对应的 suffix sum 为 [15, 14, 12, 9, 5] 或 [15, 14, 12, 9, 5, 0]
prefix sum(包含 suffix sum)的优点在于,在已经构筑 prefix sum 后,寻找任意下标所耗费的时间为 O ( 1 ) O(1) O(1)。换言之,如果给定任意 i i i,寻找 i + k i + k i+k 的子数组之和只需要花费 O ( 1 ) O(1) O(1) 的时间,其实现方法为 p r e f i x _ s u m [ i + k ] − p r e f i x _ s u m [ i − 1 ] prefix\_sum[i + k] - prefix\_sum[i - 1] prefix_sum[i+k]−prefix_sum[i−1],如:
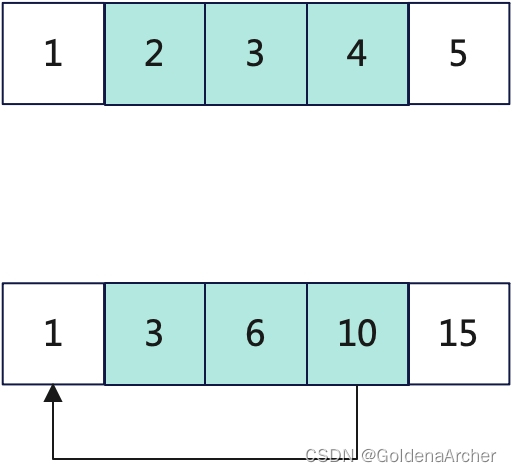
也因为这个特性,prefix sum 又可以被使用 hash map 的结构去实现。
除此之外,对 prefix array 进行其他的操作——如求平均值、最大、最小——均可以被视作 prefix sum 的变种题
prefix
仅用 prefix 一个技巧的题目有点少,1343 是一个案例:
Given an array of integers
arrand two integerskandthreshold, return the number of sub-arrays of sizekand average greater than or equal tothreshold.
这个题目的 prefix sum 解法可以用
p
r
e
f
i
x
_
s
u
m
[
i
+
k
]
−
p
r
e
f
i
x
_
s
u
m
[
i
−
1
]
prefix\_sum[i + k] - prefix\_sum[i - 1]
prefix_sum[i+k]−prefix_sum[i−1] 去找到长度为 k 的子数组之和,随后看看是不是满足条件(平均数 >= threshold)即可
对比仅用单一的 prefix sum 技巧的话,其实 sliding window 更方便一些……毕竟长度是固定的
prefix + suffix
这里面我做过的有 2909,2874,238 和 2102,题目分别如下:
2874:
You are given a 0-indexed integer array
nums.Return the maximum value over all triplets of indices
(i, j, k)such thati < j < k. If all such triplets have a negative value, return0.The value of a triplet of indices
(i, j, k)is equal to(nums[i] - nums[j]) * nums[k].
2909:
You are given a 0-indexed array
numsof integers.A triplet of indices
(i, j, k)is a mountain if:
i < j < knums[i] < nums[j] and nums[k] < nums[j]Return the minimum possible sum of a mountain triplet of
nums. If no such triplet exists, return-1.
238:
Given an integer array
nums, return an arrayanswersuch thatanswer[i]is equal to the product of all the elements ofnumsexceptnums[i].The product of any prefix or suffix of
numsis guaranteed to fit in a 32-bit integer.You must write an algorithm that runs in
O(n)time and without using the division operation.
2012:
You are given a 0-indexed integer array
nums. For each indexi(1 <= i <= nums.length - 2) the beauty ofnums[i]equals:
2, if nums[j] <nums[i] < nums[k], for all0 <= j < iand for alli < k <= nums.length - 1.1, ifnums[i - 1] < nums[i] < nums[i + 1], and the previous condition is not satisfied.0, if none of the previous conditions holds.
Return the sum of beauty of allnums[i]where1 <= i <= nums.length - 2.
其题型的主要特点就是:
- 是一个数组
- 数组可以分为 [ 0 , 1 , . . . , i ] [0, 1, ..., i] [0,1,...,i] 和 [ i , i + 1 , . . . , l e n ( a r r ) ) [i, i+1, ..., len(arr)) [i,i+1,...,len(arr)) 两段去处理
- 对所有 i i i 而言, [ 0 , 1 , . . . , i ] [0, 1, ..., i] [0,1,...,i] 和 [ i , i + 1 , . . . , l e n ( a r r ) ) [i, i+1, ..., len(arr)) [i,i+1,...,len(arr)) 的处理方式都是一样的
这里对这四道题来说也是一样的:
- 2874 是对 [ 0 , 1 , . . . , i ] [0, 1, ..., i] [0,1,...,i] 和 [ i , i + 1 , . . . , l e n ( a r r ) ) [i, i+1, ..., len(arr)) [i,i+1,...,len(arr)) 求 max
- 2909 是对 [ 0 , 1 , . . . , i ] [0, 1, ..., i] [0,1,...,i] 和 [ i , i + 1 , . . . , l e n ( a r r ) ) [i, i+1, ..., len(arr)) [i,i+1,...,len(arr)) 求 min
- 238 求的是 product sum
- 2012 则是对 [ 0 , 1 , . . . , i ] [0, 1, ..., i] [0,1,...,i] 求 max,对 [ i , i + 1 , . . . , l e n ( a r r ) ) [i, i+1, ..., len(arr)) [i,i+1,...,len(arr)) 求 min
也就是说,处理这类题型的方式可以使用 prefix array 去存储 0 -> len(nums) 的处理结果,用 suffix array(可以简化成只用一个变量) 去存储 len(nums) -> 0 的处理结果,最后筛选出满足题意的结果
hashtable + prefix sum
这种类型的基础题为 560. Subarray Sum Equals K,这道题可以说是后面很多题的一个基础,其运用的技巧就在上面提到过的:如果给定任意 i i i,寻找 i + k i + k i+k 的子数组之和只需要花费 O ( 1 ) O(1) O(1) 的时间,其实现方法为 p r e f i x _ s u m [ i + k ] − p r e f i x _ s u m [ i − 1 ] prefix\_sum[i + k] - prefix\_sum[i - 1] prefix_sum[i+k]−prefix_sum[i−1] 这一特性
之所以使用哈希表而不是数组,则是因为哈希表中保存的为 {前缀和: 前缀和出现的次数} 这一搭配,用以比较方便的寻找满足和为 k 的组合
以 560 为例,它求的是子数组之和为 k 的排列组合,这里可以将 k 视作
p
r
e
f
i
x
_
s
u
m
[
i
+
k
]
−
p
r
e
f
i
x
_
s
u
m
[
i
−
1
]
prefix\_sum[i + k] - prefix\_sum[i - 1]
prefix_sum[i+k]−prefix_sum[i−1] 的结果,哈希表中又保存的是 {前缀和: 前缀和出现的次数},因此只要通过使用 当前前缀和 - k 就能够获取
p
r
e
f
i
x
_
s
u
m
[
i
−
1
]
prefix\_sum[i - 1]
prefix_sum[i−1] 出现的次数,如:
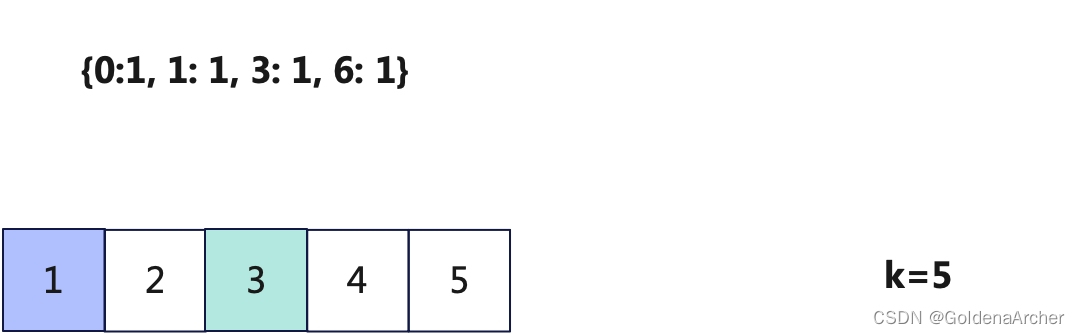
进阶篇
这里就是几种技巧的组合了
prefix + 2 pointers
这个在做过的题里面有两个:1343 Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold 和 1248 Count Number of Nice Subarrays,题目分别如下:
1248:
Given an array of integers
numsand an integerk. A continuous subarray is called nice if there arekodd numbers on it.Return the number of nice sub-arrays.
这两道题用双指针的解法比较直接,不过使用 hashtable 也可以,不过这里存的不是频率,而是 i i i 之前出现了多少个字符(不同的组合)
这道题我刚开始用的是双指针,不过后面看了下 prefix sum,写法比双指针简单
hashtable + prefix sum 变种
这里我做过的题目典型是 974,这里哈希表中保存的不是 prefix sum,而是 p r e f i x _ s u m % k prefix\_sum \% k prefix_sum%k,这样就能满足题目中 Subarray Sums Divisible by K 这一需求
原理就是,如果找到余数相同的子数组,自然也就意味着找到可以满足被 k 整除的子数组这一条件
hashtable + prefix + BST
这个体形本质上就是更多技巧的累积,相比较而言 BST 有些边界条件需要处理,总体上知道思路也能写出来(medium 范畴),题目为 437 Path Sum III
prefix + suffix + monotonic stack
这道题之前周赛出现的 2866 Beautiful Towers II,它的前置要求为能解 84 Largest Rectangle in Histogram,会 84 Largest Rectangle in Histogram 就是花时间磨一下 84 的题解套用 prefix+suffix 的技巧
简单的说一下就是从 [ 0 , 1 , . . . , i ] [0, 1, ..., i] [0,1,...,i] 和 [ i , i + 1 , . . . , l e n ( a r r ) ) [i, i+1, ..., len(arr)) [i,i+1,...,len(arr)) 分别找到最大的面积,然后二者相加即可。不过这找最大面积的技巧有些的麻烦,需要使用单调栈。如果不了解单调栈的话,这道题估计挠破脑袋都很难想到答案……
不过这道题能被归类成 medium 我是真的没想到就是了
写过的题解
- 1343 Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold
- 2874. Maximum Value of an Ordered Triplet II & 2909. Minimum Sum of Mountain Triplets II
- 238 Product of Array Except Self & 2012. Sum of Beauty in the Array
- 哈希表 - 和为 K 的子数组, leetcode 560
- 1248 Count Number of Nice Subarrays
- 974 Subarray Sums Divisible by K
- 437 Path Sum III
- 2866 Beautiful Towers II
- [python 刷题] 84 Largest Rectangle in Histogram