版本说明
当前版本号[20231107]。
| 版本 | 修改说明 |
|---|---|
| 20231107 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 对给定的两个日期之间的日期进行遍历
- 题目
- 解题思路
- 代码思路
- 参考代码
- 子集 II
- 题目
- 解题思路
- 代码思路
- 参考代码
- 填充每个节点的下一个右侧节点指针
- 题目
- 解题思路
- 代码思路
- 参考代码
对给定的两个日期之间的日期进行遍历
题目
对给定的两个日期之间的日期进行遍历,比如startTime 是 2014-07-11;endTime 是 2014-08-11 如何把他们之间的日期获取并遍历出来。
解题思路
- 首先,我们需要将给定的两个日期字符串转换为Date对象。可以使用SimpleDateFormat类来实现这个功能。
- 然后,我们需要创建一个循环来遍历这两个日期之间的所有日期。我们可以使用一个while循环,每次迭代时将当前日期加一天,直到达到结束日期。
- 在循环中,我们可以打印出当前日期,或者将其添加到一个列表中以便后续处理。
代码思路
-
定义一个名为SplitTime的公共类。
-
在SplitTime类中定义一个静态方法dateSplit,该方法接受两个参数:startDate和endDate,返回一个Date类型的列表。
private static List<Date> dateSplit(Date startDate, Date endDate) throws Exception { …… } -
在dateSplit方法中,首先判断startDate是否在endDate之前,如果不是,就不符合题意了,则抛出异常。
// 判断开始时间是否在结束时间之后,如果不是则抛出异常 if (!startDate.before(endDate)) throw new Exception("开始时间应该在结束时间之后"); -
计算startDate和endDate之间的时间差(以毫秒为单位),并将其除以一天的毫秒数(24 * 60 * 60 * 1000)得到步长step。
// 计算两个日期之间的毫秒数差值 Long spi = endDate.getTime() - startDate.getTime(); // 计算需要分割的天数 Long step = spi / (24 * 60 * 60 * 1000); -
创建一个空的Date类型的列表dateList。
// 创建一个空的日期列表 List<Date> dateList = new ArrayList<Date>(); -
将endDate添加到dateList中。
// 将结束日期添加到列表中 dateList.add(endDate); -
使用for循环进行输出每一天的日期,从1到step,每次循环都将上一个日期减去一天的毫秒数,然后将结果添加到dateList中。
// 循环分割日期,并将分割后的日期添加到列表中 for (int i = 1; i <= step; i++) { dateList.add(new Date(dateList.get(i - 1).getTime() - (24 * 60 * 60 * 1000))); } -
返回dateList。
// 返回分割后的日期列表 return dateList; -
在main方法中,创建一个SimpleDateFormat对象sdf,用于解析和格式化日期。
// 创建一个日期格式化对象 SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd"); -
使用sdf解析开始日期和结束日期,得到start和end。
// 解析开始日期和结束日期 Date start = sdf.parse("2015-4-20"); Date end = sdf.parse("2015-5-2"); -
调用dateSplit方法,传入start和end,得到分割后的日期列表lists。
// 调用dateSplit方法,获取分割后的日期列表 List<Date> lists = dateSplit(start, end); -
如果lists不为空,则遍历lists,打印每个日期。
// 判断列表是否为空,如果不为空则遍历并打印每个日期 if (!lists.isEmpty()) { for (Date date : lists) { System.out.println(sdf.format(date)); } } -
如果在执行过程中发生异常,捕获并忽略。
catch (Exception e) {}
参考代码
这段代码首先将给定的日期字符串转换为Date对象,然后使用Calendar类来遍历这两个日期之间的所有日期。在循环中,我们打印出当前日期,并将其添加到一个列表中以便后续处理。
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.ArrayList;
import java.util.Date;
import java.util.List;
public class SplitTime {
private static List<Date> dateSplit(Date startDate, Date endDate) throws Exception {
if (!startDate.before(endDate))
throw new Exception("开始时间应该在结束时间之后");
Long spi = endDate.getTime() - startDate.getTime();
Long step = spi / (24 * 60 * 60 * 1000);
List<Date> dateList = new ArrayList<Date>();
dateList.add(endDate);
for (int i = 1; i <= step; i++) {
dateList.add(new Date(dateList.get(i - 1).getTime() - (24 * 60 * 60 * 1000)));
}
return dateList;
}
public static void main(String[] args) throws ParseException {
try {
SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd");
Date start = sdf.parse("2015-4-20");
Date end = sdf.parse("2015-5-2");
List<Date> lists = dateSplit(start, end);
if (!lists.isEmpty()) {
for (Date date : lists) {
System.out.println(sdf.format(date));
}
}
} catch (Exception e) {
}
}
}
子集 II
题目
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
- 1 <= nums.length <= 10
- -10 <= nums[i] <= 10
解题思路
- 首先,我们需要创建一个空的结果列表,用于存储所有可能的子集。
- 然后,我们使用一个循环来遍历整数数组中的每个元素。对于每个元素,我们可以将其添加到当前子集中,并将其添加到结果列表中。
- 在添加元素到当前子集时,我们需要确保不重复添加相同的元素。为了实现这一点,我们可以使用一个集合来存储当前子集中的元素。每次添加元素之前,我们可以检查该元素是否已经在集合中存在。如果存在,则跳过该元素;否则,将其添加到集合和当前子集中。
- 在循环结束后,我们将当前子集添加到结果列表中。
- 最后,返回结果列表作为最终的解集。
代码思路
-
创建一个空的结果列表retList。
// 创建一个空的结果列表 List<List<Integer>> retList = new ArrayList<>(); // 添加一个空的子集到结果列表中 retList.add(new ArrayList<>()); -
如果输入数组为空或长度为0,则直接返回结果列表。
// 如果输入数组为空或长度为0,则直接返回结果列表 if (nums == null || nums.length == 0) return retList; -
对输入数组进行排序。
// 对输入数组进行排序 Arrays.sort(nums); -
创建一个临时列表tmp,用于存储当前正在处理的元素。将第一个元素添加到临时列表中,并将临时列表添加到结果列表中。
// 创建一个临时列表,用于存储当前正在处理的元素 List<Integer> tmp = new ArrayList<>(); // 将第一个元素添加到临时列表中 tmp.add(nums[0]); // 将临时列表添加到结果列表中 retList.add(tmp); -
如果输入数组只有一个元素,则直接返回结果列表。
// 如果输入数组只有一个元素,则直接返回结果列表 if (nums.length == 1) return retList; -
初始化变量lastLen,表示上一个子集的长度。
// 初始化变量 lastLen,表示上一个子集的长度 int lastLen = 1; -
遍历输入数组中的每个元素(从第二个元素开始)。
// 遍历输入数组中的每个元素(从第二个元素开始) for (int i = 1; i < nums.length; i++) -
获取当前结果列表的大小。
// 获取当前结果列表的大小 int size = retList.size(); -
如果当前元素与前一个元素不同,则更新lastLen的值。
// 如果当前元素与前一个元素不同,则更新 lastLen 的值 if (nums[i] != nums[i - 1]) { lastLen = size; } -
遍历当前结果列表中从lastLen开始的所有子集。
// 遍历当前结果列表中从 lastLen 开始的所有子集 for (int j = size - lastLen; j < size; j++) -
创建一个新的子集,并将当前元素添加到该子集中。
// 创建一个新的子集,并将当前元素添加到该子集中 List<Integer> inner = new ArrayList(retList.get(j)); inner.add(nums[i]); -
将新子集添加到结果列表中。
// 将新子集添加到结果列表中 retList.add(inner); -
返回结果列表。
// 返回结果列表
return retList;
参考代码
这段代码是一个Java类,名为Solution。它包含一个名为subsetsWithDup的方法,该方法接受一个整数数组nums作为输入,并返回一个列表,其中包含所有可能的子集(不包含重复)。
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> retList = new ArrayList<>();
retList.add(new ArrayList<>());
if (nums == null || nums.length == 0)
return retList;
Arrays.sort(nums);
List<Integer> tmp = new ArrayList<>();
tmp.add(nums[0]);
retList.add(tmp);
if (nums.length == 1)
return retList;
int lastLen = 1;
for (int i = 1; i < nums.length; i++) {
int size = retList.size();
if (nums[i] != nums[i - 1]) {
lastLen = size;
}
for (int j = size - lastLen; j < size; j++) {
List<Integer> inner = new ArrayList(retList.get(j));
inner.add(nums[i]);
retList.add(inner);
}
}
return retList;
}
}
填充每个节点的下一个右侧节点指针
题目
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例:
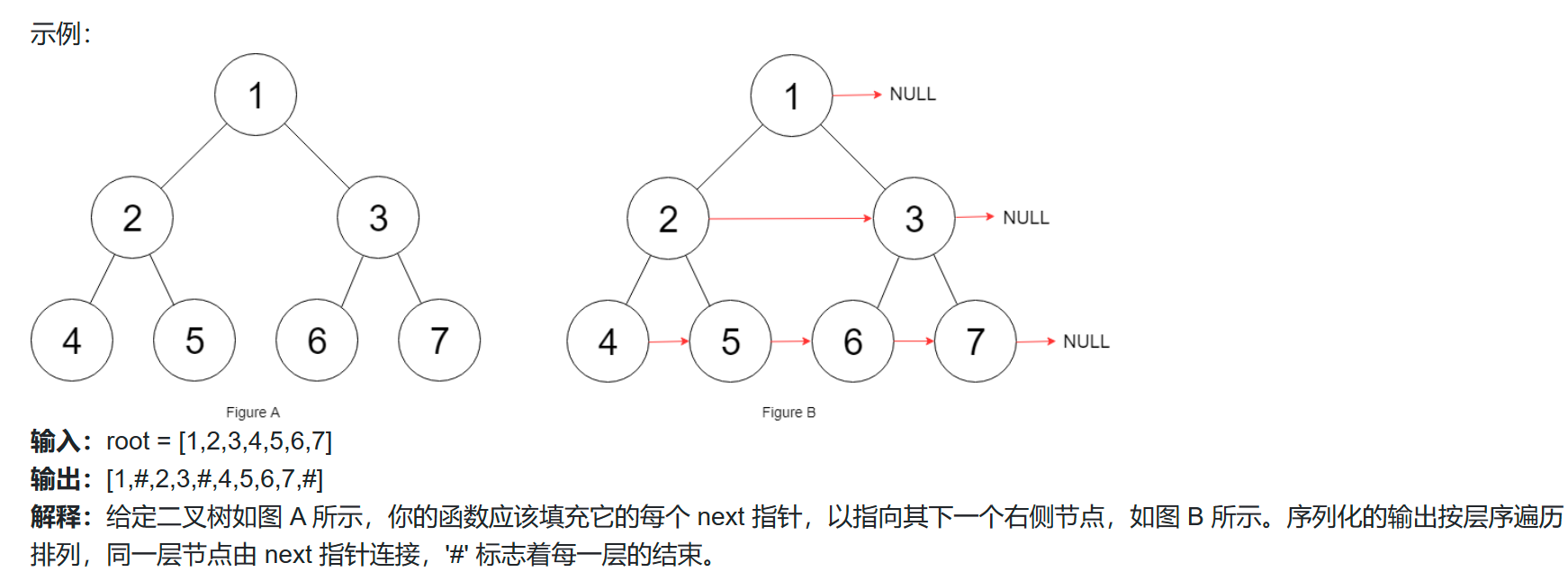
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,‘#’ 标志着每一层的结束。
提示:
树中节点的数量少于 4096
-1000 <= node.val <= 1000
解题思路
- 首先,我们需要填充完美二叉树的每个节点的next指针,使其指向其右侧的节点。如果当前节点是该层的最后一个节点,则其next指针应设置为NULL。
- 对于完美二叉树,我们可以使用层次遍历的方法来解决这个问题。具体来说,我们可以使用一个队列来存储每一层的节点。然后,我们从根节点开始,依次处理每一层的节点。对于每一层,我们将当前节点的next指针指向其右侧的节点(如果存在的话)。然后,我们将当前节点的左右子节点添加到队列中,以便在下一轮中处理。
- 在处理完一层的所有节点后,我们需要将队列中的节点清空,以便开始处理下一层的节点。
- 最后,当队列为空时,说明我们已经处理完了所有的节点,此时返回根节点即可。
代码思路
-
定义一个Node类,表示二叉树的节点,包含四个属性:val表示节点的值,left表示左子节点,right表示右子节点,next表示下一个节点。
class Node { public int val; // 节点的值 public Node left; // 左子节点 public Node right; // 右子节点 public Node next; // 下一个节点 }; -
同时定义了三个构造函数,分别用于初始化节点的值、左右子节点和下一个节点。
// 默认构造函数 public Node() { } // 带一个参数的构造函数,用于初始化节点的值 public Node(int _val) { val = _val; } // 带四个参数的构造函数,用于初始化节点的值、左右子节点和下一个节点 public Node(int _val, Node _left, Node _right, Node _next) { val = _val; left = _left; right = _right; next = _next; } -
定义一个Solution类,包含一个connect方法,用于连接二叉树中的节点。
// 定义一个Solution类,包含一个connect方法,用于连接二叉树中的节点 class Solution { public Node connect(Node root) -
首先判断根节点是否为空,如果为空则直接返回。
// 如果根节点为空,直接返回 if (root == null) return root; -
然后判断根节点的左子节点是否不为空,如果不为空则将左子节点的next指针指向右子节点。
// 如果根节点的左子节点不为空,将左子节点的next指针指向右子节点 if (root.left != null) root.left.next = root.right; -
接着判断根节点的右子节点和下一个节点是否都不为空,如果不都为空则将右子节点的next指针指向下一个节点的左子节点。
// 如果根节点的右子节点和下一个节点都不为空,将右子节点的next指针指向下一个节点的左子节点 if (root.next != null && root.right != null) { root.right.next = root.next.left; } -
最后递归地连接左子树和右子树的节点。
// 递归地连接左子树和右子树的节点 connect(root.left); connect(root.right); -
返回连接后的根节点。
// 返回连接后的根节点
return root;
参考代码
这段代码的思路是实现一个二叉树的层次遍历,并将同一层的节点通过next指针连接起来。
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {
}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
class Solution {
public Node connect(Node root) {
if (root == null)
return root;
if (root.left != null)
root.left.next = root.right;
if (root.next != null && root.right != null) {
root.right.next = root.next.left;
}
connect(root.left);
connect(root.right);
return root;
}
}