目录

树结构及其算法-二叉树节点的删除

C++代码

---

树结构及其算法-二叉树节点的删除

二叉树节点的删除操作稍为复杂，可分为以下3种情况。

1. 删除的节点为树叶，只要将其相连的父节点指向NULL即可。
2. 删除的节点只有一棵子树。
3. 删除的节点有两棵子树。要删除节点，方式有两种，虽然结果不同，但是都符合二叉树的特性。

• 找出中序立即先行者（Inorder Immediate Predecessor），就是将要删除节点的左子树中的最大者向上提。简单来说，就是从该节点的左子树往右寻找，直到右指针为NULL，这个节点就是中序立即先行者。
• 找出中序立即后继者（Inorder Immediate Successor），就是把要删除节点的右子树中的最小者向上提。简单来说，就是从该节点的右子树往左寻找，直到左指针为NULL，这个节点就是中序立即后继者。

C++代码

#include<iostream>
using namespace std;

struct TreeNode {
	int data;
	TreeNode* leftNode;
	TreeNode* rightNode;
	TreeNode(int tempData, TreeNode* tempLeftNode = nullptr, TreeNode* tempRightNode = nullptr) {
		this->data = tempData;
		this->leftNode = tempLeftNode;
		this->rightNode = tempRightNode;
	}
};

class Tree {
private:
	TreeNode* treeNode;
public:
	Tree() {
		treeNode = nullptr;
	}
	TreeNode* GetTreeNode() {
		return this->treeNode;
	}
	void AddNodeToTree(int* tempData, int tempSize) {
		for (int i = 0; i < tempSize; i++) {
			TreeNode* currentNode;
			TreeNode* newNode;
			int flag = 0;
			newNode = new TreeNode(tempData[i]);
			if (treeNode == nullptr)
				treeNode = newNode;
			else {
				currentNode = treeNode;
				while (!flag) {
					if (tempData[i] < currentNode->data) {
						if (currentNode->leftNode == nullptr) {
							currentNode->leftNode = newNode;
							flag = 1;
						}
						else
							currentNode = currentNode->leftNode;
					}
					else {
						if (currentNode->rightNode == nullptr) {
							currentNode->rightNode = newNode;
							flag = 1;
						}
						else
							currentNode = currentNode->rightNode;
					}
				}
			}
		}
	}
	void DeleteNodeToTree(TreeNode* tempTree, int tempData) {
		if (tempTree == nullptr)
			return;
		TreeNode* findNode = tempTree;
		TreeNode* pre = nullptr;
		while (findNode != nullptr) {
			if (findNode->data == tempData)
				break;
			else if (tempData < findNode->data) {
				pre = findNode;
				findNode = findNode->leftNode;
			}
			else {
				pre = findNode;
				findNode = findNode->rightNode;
			}
		}
		if (findNode == nullptr)
			return;

		if (findNode->leftNode == nullptr) {
			if (findNode == tempTree) {
				TreeNode* temp = findNode;
				findNode = findNode->rightNode;
				free(temp);
			}
			TreeNode* temp = findNode;
			(pre->data < findNode->data ? pre->rightNode : pre->leftNode) = findNode->rightNode;
			free(temp);
			temp = nullptr;
		}
		else if (findNode->rightNode == nullptr) {
			if (findNode == tempTree) {
				TreeNode* temp = findNode;
				findNode = findNode->leftNode;
				free(temp);
			}
			TreeNode* temp = findNode;
			(pre->data < findNode->data ? pre->rightNode : pre->leftNode) = findNode->leftNode;
			free(temp);
			temp = nullptr;
		}
		else {
			TreeNode* post = findNode;
			TreeNode* max = findNode->leftNode;
			while (max->rightNode != nullptr) {
				post = max;
				max = max->rightNode;
			}
			findNode->data = max->data;
			if (post == findNode)
				post->leftNode = max->leftNode;
			else
				post->rightNode = max->rightNode;
			free(max);
		}
	}
	void Inorder(TreeNode* tempTree) {
		if (tempTree != nullptr) {
			Inorder(tempTree->leftNode);
			cout << tempTree->data << " ";
			Inorder(tempTree->rightNode);
		}
	}
	TreeNode* Find(TreeNode* tree, int value) {
		while (true) {
			if (tree == nullptr)
				return nullptr;
			if (tree->data == value)
				return tree;
			else if (tree->data > value)
				tree = tree->leftNode;
			else
				tree = tree->rightNode;
		}
	}
};

int main() {
	int data[]{ 7,4,1,5,16,8,11,12,15,9,2 };
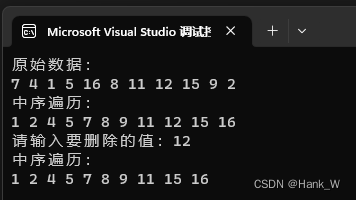
	cout << "原始数据：" << endl;
	for (int i = 0; i < 11; i++)
		cout << data[i] << " ";
	cout << endl;

	Tree* tree = new Tree;
	tree->AddNodeToTree(data, 11);

	cout << "中序遍历：" << endl;
	tree->Inorder(tree->GetTreeNode());
	cout << endl;

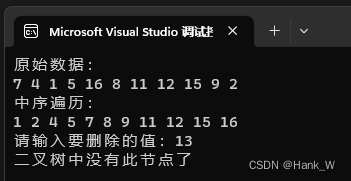
	cout << "请输入要删除的值：";
	int value;
	cin >> value;
	if ((tree->Find(tree->GetTreeNode(), value)) == nullptr)
		cout << "二叉树中没有此节点了" << endl;
	else {
		tree->DeleteNodeToTree(tree->GetTreeNode(), value);
		cout << "中序遍历：" << endl;
		tree->Inorder(tree->GetTreeNode());
		cout << endl;
	}

	return 0;
}

输出结果