首先来了解下排序二叉树的基本概念
排序二叉树:任意一个根节点,比他的左子树中的任意节点都大,比他的右子树中的任意节点都小
比如下面的这个树就是排序二叉树
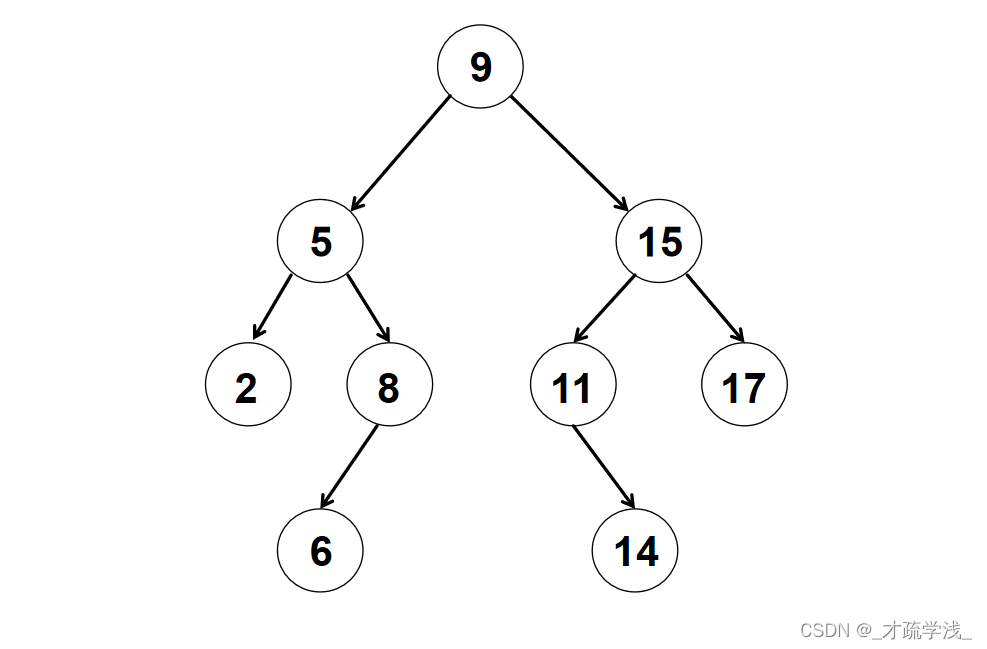
OK,在了解了这个基本概念之后,就可以去看下面的代码了
#include<iostream>
#include<stdlib.h>
using namespace std;
//树的节点结构体
typedef struct node
{
int value;
struct node* left;//左孩子
struct node* right;//右孩子
}Binary_Tree;
//向排序二叉树中添加节点
void Add_Node(Binary_Tree** tree, int num)
{
//创建一个临时节点,申请空间并进行初始化
Binary_Tree* temp = NULL;
temp = (Binary_Tree*)malloc(sizeof(Binary_Tree));
temp->value = num;
temp->left = NULL;
temp->right = NULL;
//如果该排序二叉树的根节点为空
if (*tree == NULL)
{
*tree = temp;
return;
}
Binary_Tree* pnode = *tree;
while (pnode)
{
//如果要插入的值小于该结点的数值,应放入左子树中
if (pnode->value > num)
{
//如果该结点左孩子为空
if (pnode->left == NULL)
{
pnode->left = temp;
return;
}
//如果该结点左孩子不为空,就需要往左子树的更深处去找
else
{
pnode = pnode->left;
}
}
//如果要插入的值小于该结点的数值,应放入右子树中
else if (pnode->value < num)
{
//如果该结点右孩子为空
if (pnode->right == NULL)
{
pnode->right = temp;
return;
}
//如果该结点右孩子不为空,就需要往右子树的更深处去找
else
{
pnode = pnode->right;
}
}
else
{
cout << "输入的数据与树中的节点数据存在重复,请重新输入" << endl;
free(temp);
temp = NULL;
return;
}
}
}
//建立无重复数值的排序二叉树
Binary_Tree* BST_Create()
{
int num;//节点数值
int size;//节点个数
int i;
Binary_Tree* tree = NULL;
cout << "请输入排序二叉树中结点的个数 :";
cin >> size;
cout << "请依次输入节点中的数据 :" << endl;
for (i = 0; i < size; i++)
{
cin >> num;
//向树中添加节点到正确的位置
Add_Node(&tree, num);
}
cout << "排序二叉树初始化完成" << endl;
return tree;
}
//在排序二叉树中搜索与目标数值对应的结点
void Search_AimNode(Binary_Tree* tree, int aim_num, Binary_Tree** del_node, Binary_Tree** father)
{
while (tree)
{
if (tree->value == aim_num)
{
*del_node = tree;
return;
}
//如果目标数小于该节点的数值,说明要再往左子树里去找
else if (tree->value > aim_num)
{
*father = tree;
tree = tree->left;
}
//如果大于,要往右子树去找
else if (tree->value < aim_num)
{
*father = tree;
tree = tree->right;
}
}
*father = NULL;
cout << "该排序二叉树中没有与目标数值对应的节点" << endl;
}
//排序二叉树将与aim_num数值对应的节点删除
void Node_Delete(Binary_Tree** tree , int aim_num)
{
//在查找的过程中,有一点需要注意:我们要定义一个变量,来接取该结点的根节点
//这样做的目的是如果查找的这个结点就是我们要找的目标结点的话,在该结点删除后,能够重新连接到该结点的根节点上,以建立新的排序二叉树
Binary_Tree* del_node = NULL;
Binary_Tree* father = NULL;
//查找该树中是否有与目标数值对应的节点
Search_AimNode(*tree, aim_num, &del_node, &father);
//如果没有找到对应的节点,就直接退出
if (del_node == NULL)
{
return;
}
//如果找到了对应的节点,就要考虑以下三种情况:
/*
1.这个结点没有孩子,那么直接删除这个结点就可以了
2.如果这个结点只有一个孩子,只需要将这个结点的孩子结点与根节点进行链接就可以了
3.如果这个结点有两个孩子,这个情况有两种解决办法——
①.用左子树的最大值来替代,也就是左子树的最右端结点,然后删除左子树的这个节点 ②.右子树的最小值来替代,也就是右子树的最左端结点,然后删除右子树的这个节点
为什么会有这两种解决办法呢? 这就牵涉到BST的基本概念了——任意一个父亲节点,都比他的左子树大,都比他的右子树小
所以如果对这个结点进行修改的话,我们希望在该树中找到一个一个最接近该结点大小的数值来替代他,而在排序二叉树中
左子树的最大值和右子树的最小值就是最接近这个结点大小的数值
*/
//一、2个孩子
Binary_Tree* mark = NULL;
if ((del_node->left != NULL) && (del_node->right != NULL))
{
mark = del_node;
//找左子树的最右侧节点
//先进入该结点的左子树
father = del_node;
del_node = del_node->left;
//找该左子树的最右侧结点
while (del_node->right != NULL)
{
father = del_node;
del_node = del_node->right;
}
mark->value = del_node->value;
}
//二、1个孩子或0个孩子
//这个地方需要做一个特殊处理,如果要换的结点是根节点的话,father就是NULL,要做一下特殊判断
if (father == NULL)
{
//看这个孩子是左孩子还是右孩子
//这个地方要为大家讲解一下,否则有些同学可能不太懂为什么这个地方0个孩子的情况也适用
/*
1.当左孩子不为空,右孩子为空——根节点变成当前节点的左孩子
2.当左孩子为空,右孩子不为空——根节点变成当前节点的右孩子
3.当左孩子、右孩子都为空时——根节点变成当前节点的右孩子,但右孩子为空,所以根节点也为空
*/
*tree = del_node->left ? del_node->left : del_node->right;
free(del_node);
del_node = NULL;
return;
}
//如果要删除的节点不是根节点
else
{
//如果这个结点是其根节点的左孩子
if (del_node == father->left)
{
father->left = del_node->left ? del_node->left : del_node->right;
}
//如果这个结点是其根节点的右孩子
if (del_node == father->right)
{
father->right = del_node->left ? del_node->left : del_node->right;
}
free(del_node);
del_node = NULL;
return;
}
}
//中序遍历
void Inorder_Traversal(Binary_Tree* pTree)
{
//左、根、右
if (pTree == NULL)
{
return;
}
//左子树
Inorder_Traversal(pTree->left);
//节点打印,也就是打印根节点的数据
cout << pTree->value << " ";
//右子树
Inorder_Traversal(pTree->right);
}
int main()
{
Binary_Tree* tree = NULL;
tree = BST_Create();
cout << "中序遍历的结果为:";
Inorder_Traversal(tree);
cout << endl;
int aim_num;
cout << "请输入你想要删除的的目标数据 : ";
cin >> aim_num;
Node_Delete(&tree, aim_num);
cout << "该树的中序遍历结果为 : ";
Inorder_Traversal(tree);
return 0;
}以上就是本篇博客的全部内容了,大家有什么地方没有看懂的话,可以在评论区留言给我,咱要力所能及的话就帮大家解答解答
今天的学习记录到此结束啦,咱们下篇文章见,ByeBye!