目录

前言

一、 二维差分的定义

二、二维差分的使用

三、计算二维差分

四、ACWing 798. 差分矩阵

---

---

前言

一维+二维前缀和详解

图文详解一维差分

一、 二维差分的定义

对于一个给定的二维数组 arr，它的二维差分数组 d 中 d[i][j] 可以用如下公式计算：

①

② 

③ 

④

实际上，上面的公式是通过二维数组 arr 是二维差分数组的前缀和这个条件推导出来的，因此，不像一维差分定义那样直观。

二、二维差分的使用

二维差分的主要用处：快速地将一个区块中的所有元素都加上一个值 v。

使用差分可以将在数组 arr 上的区块操作转化为在差分数组 d 上的单点操作。转换方式如下：

假设区块左上角坐标为 (x1, y1)，右下角坐标为 (x2, y2)，对该区块中的每个元素都加上 v 等价于下面四个操作：

1.

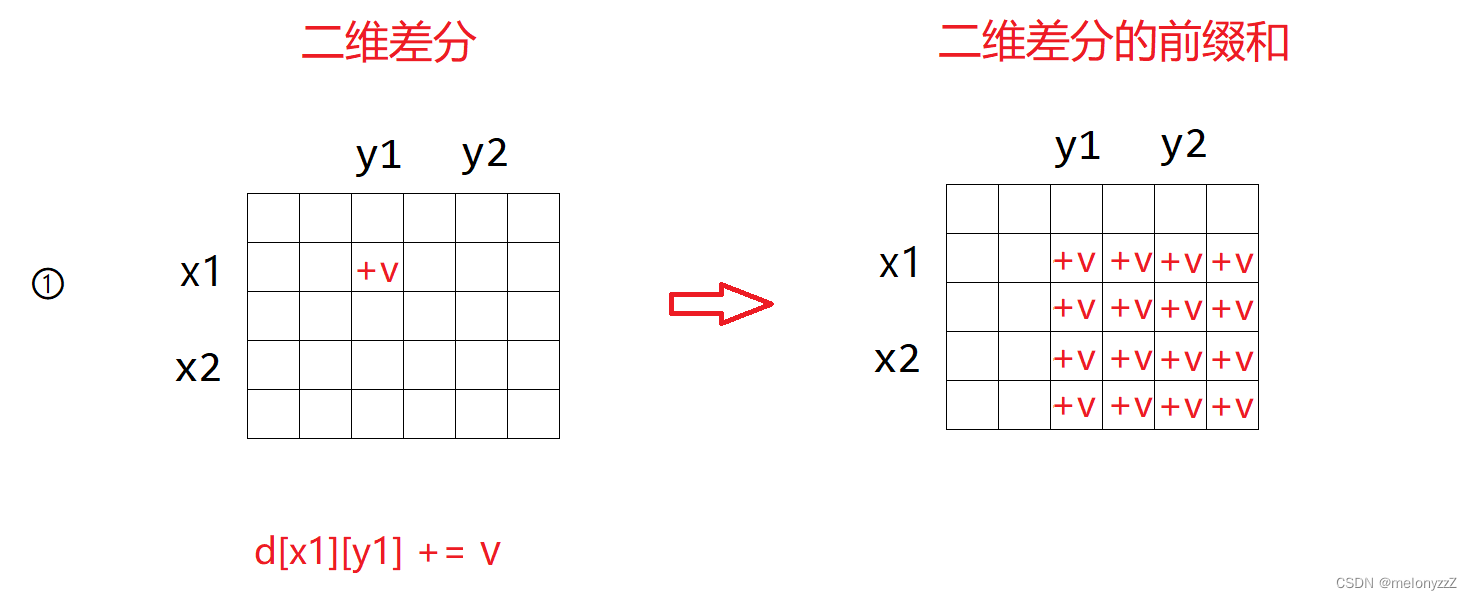
2.

 

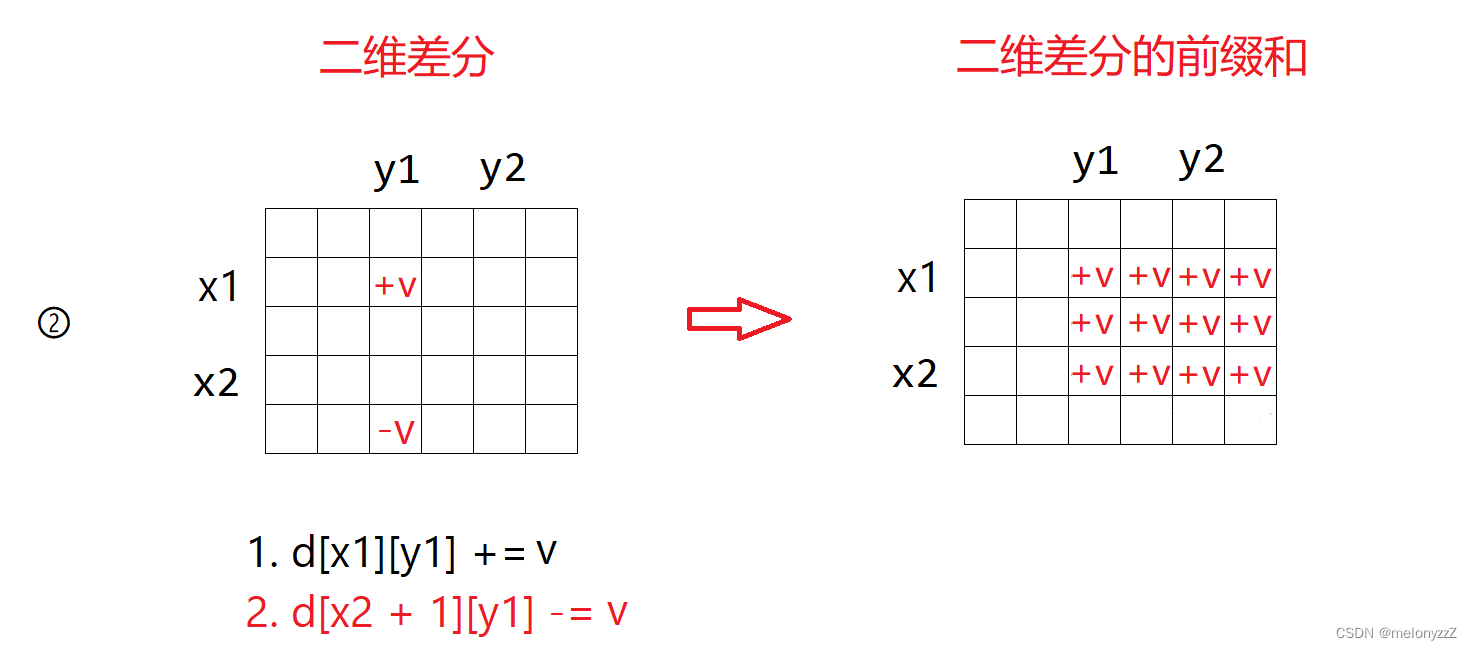
 3.

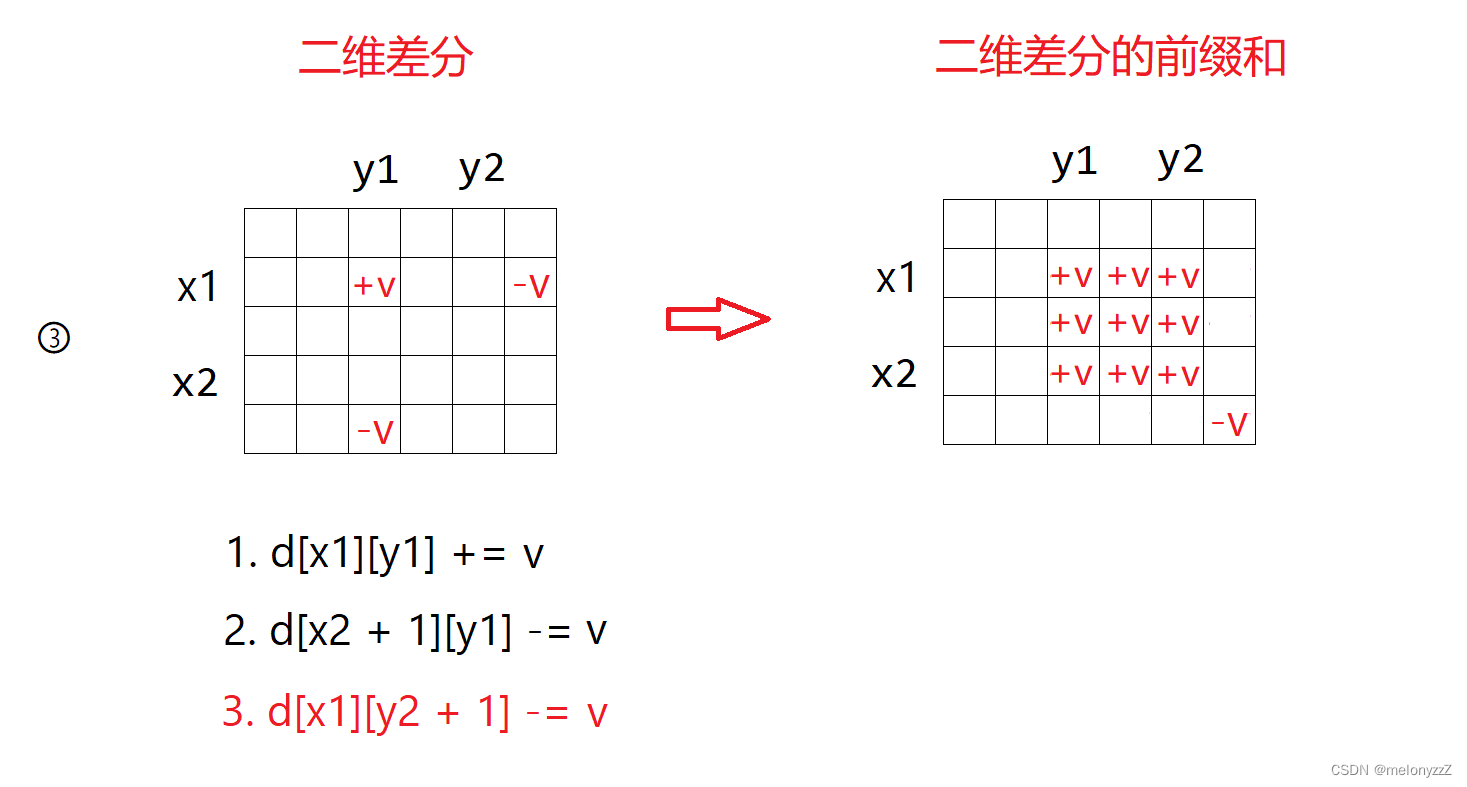
4.

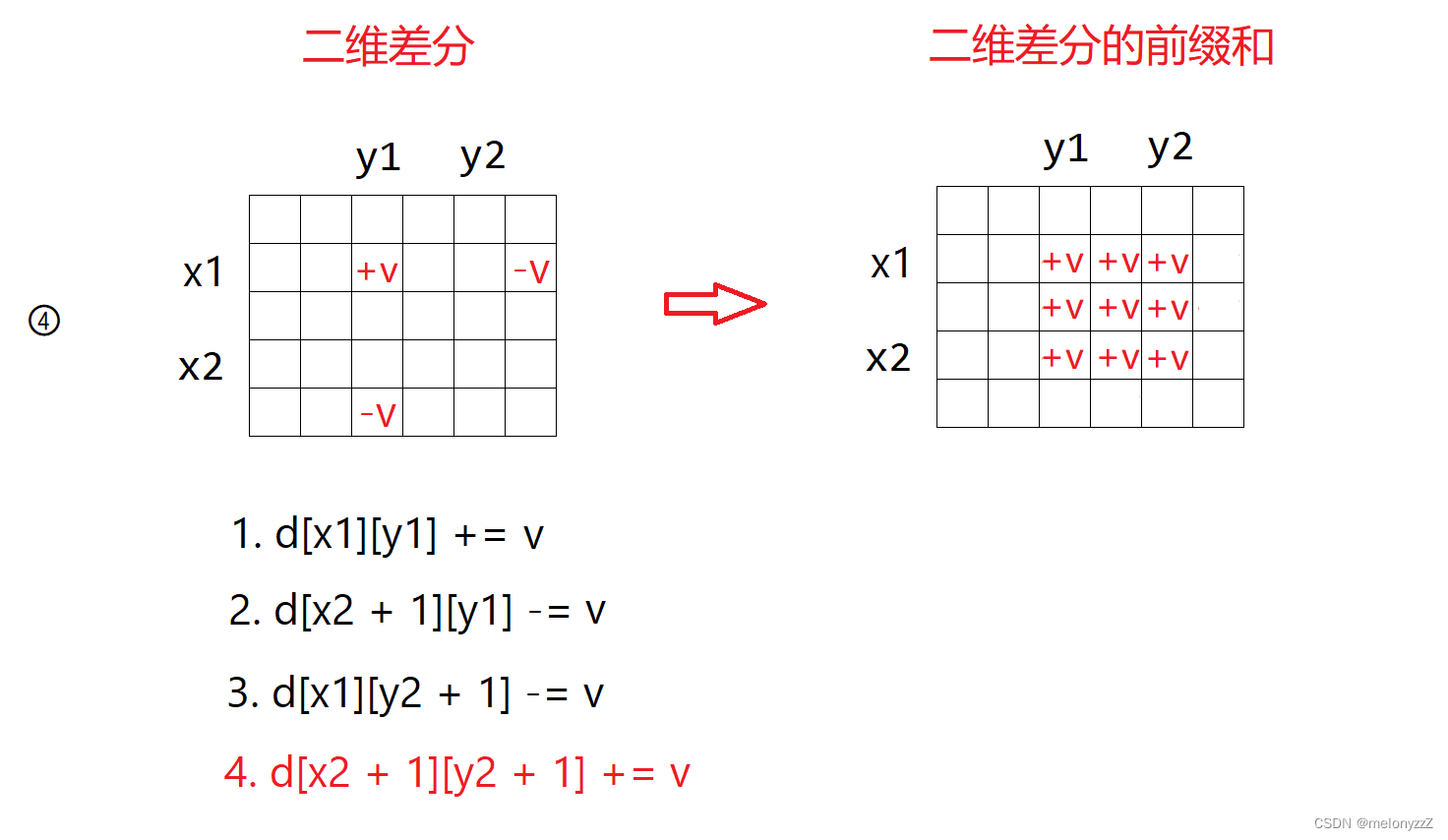 因为差分数组的前缀和相当于原数组，所以对差分数组进行以上四个单点操作后，就相当于给数组 arr 的区块加上一个值 v。

三、计算二维差分

通过定义计算二维差分比较复杂，可以使用一种更巧妙的方法：将二维差分中的每个元素一个一个地插进去。

1. 首先假设原二维数组 arr 的元素全为 0，那么二维差分数组 d 的元素显然也全为 0，这样完全符合定义。

2. 接下来将 arr 中的每个元素依次更新为实际值。例如 arr[2][3] 的实际值为 5，那么就相当于给以 (2, 3) 坐标为左上角，(2, 3) 坐标为右下角的区块中的所有元素加上 5。

   ① d[2][3] += 5

   ② d[3][3] -= 5

   ③ d[2][4] -= 5

   ④ d[3][4] += 5

   这样便得到了整个差分数组。

四、ACWing 798. 差分矩阵

题目描述：

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1, y1, x2, y2, c，其中 (x1, y1) 和 (x2, y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式：

第一行包含整数 n, m, q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1, y1, x2, y2, c，表示一个操作。

输出格式：

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围：

1 ≤ n, m ≤1000, 1 ≤ q ≤100000, 0 ≤ x1 ≤ x2 ≤ n - 1, 0 ≤ y1 ≤ y2 ≤ m - 1, −1000 ≤ c ≤ 1000, −1000 ≤ 矩阵内元素的值 ≤ 1000

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
0 0 1 1 1
0 2 1 2 2
2 0 2 3 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

代码实现： 

#include <stdio.h>

int arr[1000][1000];  
int d[1001][1001];

void insert(int x1, int y1, int x2, int y2, int c)
{
	d[x1][y1] += c;
	d[x2 + 1][y1] -= c;
	d[x1][y2 + 1] -= c;
	d[x2 + 1][y2 + 1] += c;
}

int main()
{
	int n = 0, m = 0, q = 0;
	scanf("%d %d %d", &n, &m, &q);
	int i = 0;
	int j = 0;
	// 输入整数矩阵，并计算二维差分
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < m; j++)
		{
			scanf("%d", &arr[i][j]);
			insert(i, j, i, j, arr[i][j]);
		}
	}
	// 进行 q 次操作
	while (q--)
	{
		int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
		int c = 0;
		scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &c);
		insert(x1, y1, x2, y2, c);
	}	
	// 计算二维差分的前缀和，即原二维数组 arr
	arr[0][0] = d[0][0];
	for (j = 1; j < m; j++)
	{
		arr[0][j] = arr[0][j - 1] + d[0][j];
	}
	for (i = 1; i < n; i++)
	{
		arr[i][0] = arr[i - 1][0] + d[i][0];
	}
	for (i = 1; i < n; i++)
	{
		for (j = 1; j < m; j++)
		{
			arr[i][j] = arr[i - 1][j] + arr[i][j - 1] - arr[i - 1][j - 1] + d[i][j];
		}
	}
	// 输出
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < m; j++)
		{
			printf("%d ", arr[i][j]);
		}
		printf("\n");
	}
	return 0;
}