2500. 删除每行中的最大值
给你一个 m x n 大小的矩阵 grid ,由若干正整数组成。
执行下述操作,直到 grid 变为空矩阵:
- 从每一行删除值最大的元素。如果存在多个这样的值,删除其中任何一个。
- 将删除元素中的最大值与答案相加。
注意 每执行一次操作,矩阵中列的数据就会减 1 。
返回执行上述操作后的答案。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 100
示例:
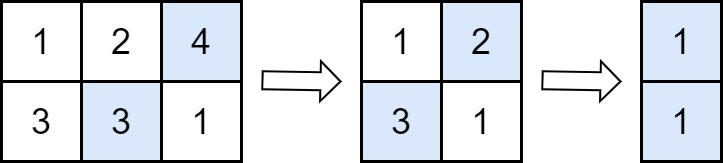
输入:grid = [[1,2,4],[3,3,1]]
输出:8
解释:上图展示在每一步中需要移除的值。
- 在第一步操作中,从第一行删除 4 ,从第二行删除 3(注意,有两个单元格中的值为 3 ,我们可以删除任一)。在答案上加 4 。
- 在第二步操作中,从第一行删除 2 ,从第二行删除 3 。在答案上加 3 。
- 在第三步操作中,从第一行删除 1 ,从第二行删除 1 。在答案上加 1 。
最终,答案 = 4 + 3 + 1 = 8 。
思路:
直接对每一行元素进行排序,然后遍历一次即可。时间复杂度 O ( m n l o g n ) O(mnlogn) O(mnlogn)
class Solution {
public:
int deleteGreatestValue(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
// 每一行元素从小到大排序
for (auto& row : grid) sort(row.begin(), row.end());
int ans = 0;
// 从最右侧的列开始, 每次删除某列, 并取该列的最大值
for (int i = n - 1; i >= 0; i--) {
int mx = 0;
for (int j = 0; j < m; j++) mx = max(mx, grid[j][i]);
ans += mx;
}
return ans;
}
};
2501. 数组中最长的方波
给你一个整数数组 nums 。如果 nums 的子序列满足下述条件,则认为该子序列是一个 方波 :
- 子序列的长度至少为
2,并且 - 将子序列从小到大排序 之后 ,除第一个元素外,每个元素都是前一个元素的 平方 。
返回 nums 中 最长方波 的长度,如果不存在 方波 则返回 -1 。
子序列 也是一个数组,可以由另一个数组删除一些或不删除元素且不改变剩余元素的顺序得到。
提示:
2 <= nums.length <= 10^52 <= nums[i] <= 10^5
示例:
输入:nums = [4,3,6,16,8,2]
输出:3
解释:选出子序列 [4,16,2] 。排序后,得到 [2,4,16] 。
- 4 = 2 * 2.
- 16 = 4 * 4.
因此,[4,16,2] 是一个方波.
可以证明长度为 4 的子序列都不是方波。
思路:
排序+递推。
由于方波子序列的内部是顺序无关的,只要排序后满足后一个数是前一个数的平方即可。那么,很自然的,我们可以先对整个数组排个序。
我们可以用动态规划的思维来看待这道题。
设f[i]表示以nums[i]作为结尾的方波子序列的最大长度。我们考虑状态转移时,对于f[i],既然是以nums[i]结尾,那么我们考虑方波子序列的倒数第二个数。倒数第二个数只能是nums[i]的平方根。
考虑到这,好像f[i]中的i表示下标不是很合适。应该用i直接表示数字。即,f[i]表示,以数字i结尾的,最长的方波子序列的长度。状态转移为:f[i] = f[sqrt(i)] + 1。
这样来看,需要开根号,为了避免开根号产生可能的浮点数,我们不开根号(并且开根号的运算量并不是 O ( 1 ) O(1) O(1)的),而选用开根号的逆运算,平方。
那我们的状态表示就要倒着来了,设f[i]表示以数字i开头的,最长的方波子序列的长度。状态转移,我们考虑子序列的第二个数,则f[i] = f[i * i] + 1。
i的状态依赖于i * i,那么我们状态的计算要从大到小进行。
由于状态表示中的i是数字,而不是下标。数字与下标不同,下标是连续的,我们可以开一个数组来存储状态;而数字是离散的,那么我们采用一个哈希表来存储状态即可。
总的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),主要是排序的时间开销,后续状态计算由于使用了哈希表,只需要一次遍历,复杂度为 O ( n ) O(n) O(n)
typedef long long LL;
class Solution {
public:
int longestSquareStreak(vector<int>& nums) {
int n = nums.size(), ans = 1;
sort(nums.begin(), nums.end());
unordered_map<int, int> f; // f[i] = x 表示以数字i开头的方波子序列的最长长度为x
// 从大到小遍历整个数组, 并更新哈希表
for (int i = n - 1; i >= 0; i--) {
int x = nums[i];
// 若 x * x 超过 int 限制, 或者 f 中不存在 x * x, 则初始化其长度为1
if (x >= INT_MAX / x || !f.count(x * x)) f[x] = 1;
else f[x] = f[x * x] + 1;
ans = max(ans, f[x]);
}
return ans == 1 ? -1 : ans;
}
};
2502. 设计内存分配器
给你一个整数 n ,表示下标从 0 开始的内存数组的大小。所有内存单元开始都是空闲的。
请你设计一个具备以下功能的内存分配器:
- 分配 一块大小为
size的连续空闲内存单元并赋 idmID。 - 释放 给定 id
mID对应的所有内存单元。
注意:
- 多个块可以被分配到同一个
mID。 - 你必须释放
mID对应的所有内存单元,即便这些内存单元被分配在不同的块中。
实现 Allocator 类:
Allocator(int n)使用一个大小为n的内存数组初始化Allocator对象。int allocate(int size, int mID)找出大小为size个连续空闲内存单元且位于 最左侧 的块,分配并赋 idmID。返回块的第一个下标。如果不存在这样的块,返回-1。int free(int mID)释放 idmID对应的所有内存单元。返回释放的内存单元数目。
提示:
1 <= n, size, mID <= 1000- 最多调用
allocate和free方法1000次
示例:
输入
["Allocator", "allocate", "allocate", "allocate", "free", "allocate", "allocate", "allocate", "free", "allocate", "free"]
[[10], [1, 1], [1, 2], [1, 3], [2], [3, 4], [1, 1], [1, 1], [1], [10, 2], [7]]
输出
[null, 0, 1, 2, 1, 3, 1, 6, 3, -1, 0]
解释
Allocator loc = new Allocator(10); // 初始化一个大小为 10 的内存数组,所有内存单元都是空闲的。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 0 。内存数组变为 [1, , , , , , , , , ]。返回 0 。
loc.allocate(1, 2); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,2, , , , , , , , ]。返回 1 。
loc.allocate(1, 3); // 最左侧的块的第一个下标是 2 。内存数组变为 [1,2,3, , , , , , , ]。返回 2 。
loc.free(2); // 释放 mID 为 2 的所有内存单元。内存数组变为 [1, ,3, , , , , , , ] 。返回 1 ,因为只有 1 个 mID 为 2 的内存单元。
loc.allocate(3, 4); // 最左侧的块的第一个下标是 3 。内存数组变为 [1, ,3,4,4,4, , , , ]。返回 3 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,1,3,4,4,4, , , , ]。返回 1 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 6 。内存数组变为 [1,1,3,4,4,4,1, , , ]。返回 6 。
loc.free(1); // 释放 mID 为 1 的所有内存单元。内存数组变为 [ , ,3,4,4,4, , , , ] 。返回 3 ,因为有 3 个 mID 为 1 的内存单元。
loc.allocate(10, 2); // 无法找出长度为 10 个连续空闲内存单元的空闲块,所有返回 -1 。
loc.free(7); // 释放 mID 为 7 的所有内存单元。内存数组保持原状,因为不存在 mID 为 7 的内存单元。返回 0 。
思路:
比赛时,我的想法是:用链表来维护空闲的内存块和已经被分配出去的内存块,其中对于某一个id所持有的你存块,用一个哈希表来存储。
内存分配时,只要沿着空闲内存块的链表依次进行遍历查找,找到第一块大小足够的内存块,然后进行切分出去就好了。难点主要在于内存回收时,当一块内存被释放,则需要将其重新加入到空闲链表中,而如果这个内存块与前面或者后面的内存块相邻,则需要进行内存块的合并。
先暂且不考虑时间复杂度,这样的做法应当是行得通的,然而我可能是一些细节和边界没有处理好,提交一直WA,一直坐牢到比赛结束。现在尝试用这种思路重写一遍代码(改用更熟悉的 Java 来写这道题)。提交报了WA,对照着错误数据打断点进行debug,一行一行的观察,最后发现是释放内存时,将内存块重新插入空闲链表时,判断条件写错了。
这种类型的题目,真的很考察编码功底和细节处理能力。稍不注意就会出错。(一开始free方法里我都忘了从哈希表中将对应的键值进行移除,真是惭愧)
力扣上类似的题目还有,实现一个LRU,LFU
// Java
// 10ms 42.3MB
class Allocator {
// 内存块节点
class Node {
int begin;
int end;
Node pre;
Node next;
Node(int begin, int end) {
this.begin = begin;
this.end = end;
}
}
// 空闲内存链表
Node freeHead;
Node freeTail;
// 已被占用的内存块
Map<Integer, List<Node>> used;
// 将一个内存块重新插入空闲链表
private void insertToFreeList(Node e) {
Node pre = freeHead, cur = freeHead.next;
// 找到需要插入的位置
while (cur.end <= e.begin) {
// 刚开始这里的判断条件写错了, 写成 > 了, 调试了半天
pre = pre.next;
cur = cur.next;
}
// 插入这个节点
e.pre = pre;
e.next = pre.next;
e.pre.next = e;
e.next.pre = e;
// 进行可能的合并
for (int i = 0; i < 2; i++) {
if (pre.end == e.begin) {
// 合并
pre.end = e.end;
pre.next = e.next;
e.next.pre = pre;
e.next = e.pre = null; // 彻底断干净
e = pre.next;
} else {
pre = e;
e = e.next;
}
}
}
// 分配内存时, 从一个已找到的内存块中进行切割
private void cutOff(Node e, int mID, int size) {
int cutBegin = e.begin, cutEnd = e.begin + size;
if (cutEnd == e.end) {
// 整块直接切掉
e.pre.next = e.next;
e.next.pre = e.pre;
e.next = e.pre = null; // 断干净
} else {
// 切掉后还剩一小块
e.begin = cutEnd;
}
// 将切下的这一块内存加入到哈希表
if (!used.containsKey(mID)) used.put(mID, new ArrayList<>());
used.get(mID).add(new Node(cutBegin, cutEnd));
}
public Allocator(int n) {
freeHead = new Node(-1, -1);
freeTail = new Node(n + 1, n + 1);
freeHead.next = freeTail;
freeTail.pre = freeHead;
insertToFreeList(new Node(0, n)); // 空闲链表中初始化一块内存
used = new HashMap<>();
}
public int allocate(int size, int mID) {
Node cur = freeHead.next;
// 找到第一块>= size的空闲内存块
while (cur != freeTail) {
if (cur.end - cur.begin >= size) break;
else cur = cur.next;
}
// 没找到
if (cur.end - cur.begin < size) return -1;
// 找到了
int ret = cur.begin;
// 切掉一块内存
cutOff(cur, mID, size);
return ret;
}
public int free(int mID) {
// 不存在mID对应的内存单元
if (!used.containsKey(mID) || used.get(mID).isEmpty()) return 0;
// 重新插入到 freeList
int sum = 0;
for (Node e : used.get(mID)) {
sum += e.end - e.begin;
insertToFreeList(e);
}
used.get(mID).clear(); // 从哈希表中删除
return sum;
}
}
随后,我看了排名靠前的几位大佬的代码,给跪了!大佬们的思路都很简洁,只开了一个数组,然后如果某个内存块被分配给了某个mID,则在对应的位置打上标记。真的太简洁了,在打周赛时,应该采用尽可能简单的思路,在短时间内通过题目才是正道。(这道题目数据范围比较小(1000的数据范围,可以直接用
O
(
n
2
)
O(n^2)
O(n2) 的做法),所以可以直接暴力做)
如果数据范围大的话,考察的就是数据结构了,可能需要用到平衡树等来做,就比较难了。
// Java
// 24ms 42.3MB
class Allocator {
private int[] A;
public Allocator(int n) {
A = new int[n];
}
public int allocate(int size, int mID) {
int cnt = 0;
for (int i = 0; i < A.length; i++) {
if (A[i] == 0) cnt++;
else cnt = 0;
if (cnt == size) {
for (int j = i - size + 1; j <= i; j++) A[j] = mID;
return i - size + 1;
}
}
return -1;
}
public int free(int mID) {
int cnt = 0;
for (int i = 0; i < A.length; i++) {
if (A[i] == mID) {
A[i] = 0;
cnt++;
}
}
return cnt;
}
}
2503. 矩阵查询可获得的最大分数
给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。
找出一个大小为 k 的数组 answer ,且满足对于每个整数 queres[i] ,你从矩阵 左上角 单元格开始,重复以下过程:
- 如果
queries[i]严格 大于你当前所处位置单元格,如果该单元格是第一次访问,则获得 1 分,并且你可以移动到所有4个方向(上、下、左、右)上任一 相邻 单元格。 - 否则,你不能获得任何分,并且结束这一过程。
在过程结束后,answer[i] 是你可以获得的最大分数。注意,对于每个查询,你可以访问同一个单元格 多次 。
返回结果数组 answer 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 10^5k == queries.length1 <= k <= 10^41 <= grid[i][j], queries[i] <= 10^6
示例:

输入:grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
输出:[5,8,1]
解释:上图展示了每个查询中访问并获得分数的单元格。
思路:
这其实是一个连通块问题,对于每个询问x,可以把矩阵中所有大于x的格子都看成障碍物,然后此次询问的答案就是从左上角能到达的连通块的大小。(每个格子只有在第一次访问时才获得1分,并且走过的格子可以重复走,也就是说,某一次的queries[i],要求的时从左上角开始走,能走到的连通块的格子的数量,并且连通块里所有格子都不能超过queries[i])
很明显,若有queries[i] < queries[j],那么,在queris[i]限制下能走到的全部格子,在queries[j]下也能全部走到。
所以,我们可以先将queries数组从小到大排个序,由于后一个queries一定比前一个queris大,那么能走到的格子数总是递增的。
对于访问格子,我们可以
-
用并查集对相邻的格子进行合并,并维护连通块的大小;
-
也可以用一个小根堆,来存储当前所有可能访问的格子,并每次针对当前
queries的限制,不断从小根堆中取出不超过queries的格子进行访问。
两种思路的核心都在于:要先观察出,需要对查询进行离线处理(不是每次查询都要做一次操作,而是先把全部查询缓存下来,然后一次性求出所有查询的结果)
解法一:离线查询 + 并查集
// 348ms
// 维护点权
class Solution {
public:
vector<int> p;
vector<int> cnt; // 连通块中点的个数
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
vector<int> maxPoints(vector<vector<int>>& grid, vector<int>& queries) {
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int k = queries.size(), m = grid.size(), n = grid[0].size(), mn = m * n;
vector<int> qPos(k);
vector<int> gPos(mn);
for (int i = 0; i < k; i++) qPos[i] = i;
for (int i = 0; i < mn; i++) gPos[i] = i;
// 对queries从小到大排序
sort(qPos.begin(), qPos.end(), [&](int a, int b) {
return queries[a] < queries[b];
});
// 对矩阵中全部的点, 按照val从小到大排序, 二维坐标一维化
sort(gPos.begin(), gPos.end(), [&](int a, int b) {
return grid[a / n][a % n] < grid[b / n][b % n];
});
// 并查集初始化
p.resize(mn);
cnt.resize(mn);
for (int i = 0; i < mn; i++) {
p[i] = i;
cnt[i] = 1;
}
vector<int> ans(k);
// 从小到大处理每个queries
for (int i = 0, j = 0; i < k; i++) {
int limit = queries[qPos[i]];
int s = j; // 记录矩阵中点的开始位置
while (j < mn && grid[gPos[j] / n][gPos[j] % n] < limit) j++;
// 对于 [s, j) 中的所有点, 都可以进行并查集合并(往4个方向)
for (int t = s; t < j; t++) {
int u = gPos[t];
int x = u / n, y = u % n;
for (int o = 0; o < 4; o++) {
int nx = x + dx[o];
int ny = y + dy[o];
if (nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] >= limit) continue;
// 尝试合并
int nu = nx * n + ny;
int pu = find(u), pnu = find(nu);
if (pu != pnu) {
p[pu] = pnu;
cnt[pnu] += cnt[pu];
}
}
}
// 操作结束后, 看下左上角的格子所在的连通块的情况即可
int root = find(0);
if (grid[0][0] >= limit) ans[qPos[i]] = 0; // 左上角格子本身>=limit, 则答案不应该是1, 而是0
else ans[qPos[i]] = cnt[root];
}
return ans;
}
};
有另一种做法可以稍加记录,改成维护边,当某两个相邻的点,这两个点的值都小于queris时,则这两个点在这次询问中可以被纳入。
我们将每两个点之间连一条边,设这个边的权重为两个点中较大的值。那么当某条边小于queries时,可以将这条边上的两个点进行合并。
对于如何建边,我们可以对于每个点,只建其左侧和上侧的边,这样就能保证不重复建边,并且2个点之间的边,我们只建一条,而不建2条无向边。
// 296ms
typedef pair<int, pair<int ,int>> PIII;
class Solution {
public:
vector<int> p;
vector<int> cnt;
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
vector<int> maxPoints(vector<vector<int>>& grid, vector<int>& queries) {
int k = queries.size(), m = grid.size(), n = grid[0].size(), mn = m * n;
vector<int> qPos(k);
for (int i = 0; i < k; i++) qPos[i] = i;
sort(qPos.begin(), qPos.end(), [&](int a, int b) {
return queries[a] < queries[b];
});
// 每条边, 需要维护边权(用于从小到大排序), 也要维护左右两个端点(用于合并), 所以需要3个数
vector<PIII> edges;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int u = i * n + j; // 二维坐标一维化
// 对当前点的上方邻接点进行建边
if (i > 0) edges.push_back({max(grid[i][j], grid[i - 1][j]), {u, u - n}});
// 对当前点的左侧邻接点进行建边
if (j > 0) edges.push_back({max(grid[i][j], grid[i][j - 1]), {u, u - 1}});
}
}
// 对边按照边权从小到大排序
sort(edges.begin(), edges.end());
// 并查集初始化
p.resize(mn);
cnt.resize(mn);
for (int i = 0; i < mn; i++) {
p[i] = i;
cnt[i] = 1;
}
vector<int> ans(k);
for (int i = 0, j = 0; i < k; i++) {
int limit = queries[qPos[i]];
int s = j;
while (j < edges.size() && edges[j].first < limit) j++;
// 找到当前可以合并的最后一条边
for (int t = s; t < j; t++) {
int a = edges[t].second.first, b = edges[t].second.second;
int pa = find(a), pb = find(b);
if (pa != pb) {
p[pa] = pb;
cnt[pb] += cnt[pa];
}
}
if (grid[0][0] >= limit) ans[qPos[i]] = 0;
else ans[qPos[i]] = cnt[find(0)];
}
return ans;
}
};
解法二:离线查询 + 小根堆
这里对于queries的处理换一种方式,换成使用pair来同时保存元素大小和数组下标
typedef pair<int, int> PII;
class Solution {
public:
vector<int> maxPoints(vector<vector<int>>& grid, vector<int>& queries) {
int k = queries.size(), m = grid.size(), n = grid[0].size(), mn = m * n;
vector<PII> q(k);
for (int i = 0; i < k; i++) q[i] = {queries[i], i};
sort(q.begin(), q.end());
priority_queue<PII, vector<PII>, greater<PII>> heap;
vector<bool> st(mn); // 标记某个格子是否被访问过了
heap.push({grid[0][0], 0}); // 把第一个点插进去
st[0] = true;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
vector<int> ans(k);
int cnt = 0; // 当前已经访问了多少个点了
for (int i = 0; i < k; i++) {
int limit = q[i].first, pos = q[i].second;
while (!heap.empty() && heap.top().first < limit) {
// 可以访问这个点, 并且扩展它
int u = heap.top().second; // 获取这个点的下标
heap.pop();
cnt++;
int x = u / n, y = u % n;
for (int j = 0; j < 4; j++) {
int nx = x + dx[j], ny = y + dy[j];
if (nx < 0 || nx >= m || ny < 0 || ny >= n || st[nx * n + ny]) continue;
heap.push({grid[nx][ny], nx * n + ny});
st[nx * n + ny] = true;
}
}
ans[pos] = cnt;
}
return ans;
}
};
其实st数组也可以省掉,因为矩阵中元素的值都是大于0的,我们可以在访问后直接将其置为0
typedef pair<int, int> PII;
class Solution {
public:
vector<int> maxPoints(vector<vector<int>>& grid, vector<int>& queries) {
int k = queries.size(), m = grid.size(), n = grid[0].size(), mn = m * n;
vector<PII> q(k);
for (int i = 0; i < k; i++) q[i] = {queries[i], i};
sort(q.begin(), q.end());
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({grid[0][0], 0}); // 把第一个点插进去
grid[0][0] = 0;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
vector<int> ans(k);
int cnt = 0; // 当前已经访问了多少个点了
for (int i = 0; i < k; i++) {
int limit = q[i].first, pos = q[i].second;
while (!heap.empty() && heap.top().first < limit) {
// 可以访问这个点, 并且扩展它
int u = heap.top().second; // 获取这个点的下标
heap.pop();
cnt++;
int x = u / n, y = u % n;
for (int j = 0; j < 4; j++) {
int nx = x + dx[j], ny = y + dy[j];
if (nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] == 0) continue;
heap.push({grid[nx][ny], nx * n + ny});
grid[nx][ny] = 0;
}
}
ans[pos] = cnt;
}
return ans;
}
};
这道题又用到了对于数组下标进行排序这种处理技巧,当然也可以使用pair。
这种技巧常用于,需要进行排序,但同时需要保留原下标的场景。
另外需要注意,在维护某个点时,我们还用到了二维坐标和一维坐标之间进行相互转换的技巧。
总结
holy shit!本场周赛太拉跨了,只做出2题。
T1是排序+模拟;T2是排序+递推(有点动态规划的意味);T3可以直接暴力做;T4是连通块问题。
本次周赛,T3其实没有T2难,但T3我一直没通过。
一是没注意到数据范围,也没想到可以直接用数组对内存分配进行暴力模拟;二是coding熟练度还不够,一些细节的处理不是特别好,coding中容易写错变量或者判断条件,然后需要花大量时间才能找到问题所在。比较可惜。
T4听完并消化一些大佬的讲解后,发现难度不算大;做不出来,主要还是练的题不够多。T4读完题后我其实有一定感觉,能想到一部分思路,但还是无法把整个思路走通,有些地方还是存在一些思维的差距,仍然需要勤加练习。