对称式ICP

写在前面的话

针对于局部平面不完美的情况，提出了一种对称式ICP目标函数，相较于传统的ICP方法，增大了收敛域，提高了收敛速度。论文理论说明不甚清楚，实验较少，但代码开源。

理论

对称目标函数

在icp中对于一对对应点p，q：在点到法线的度量中：
$$(p-q)\cdot n_q\text{\hspace{1em}(3)}$$
只有当局部表面是一个完美平面时上式才成立，因此提出一种标准对称式度量：
$$(p-q)\cdot \left(n_p+n_q\right).\text{\hspace{1em}(4)}$$

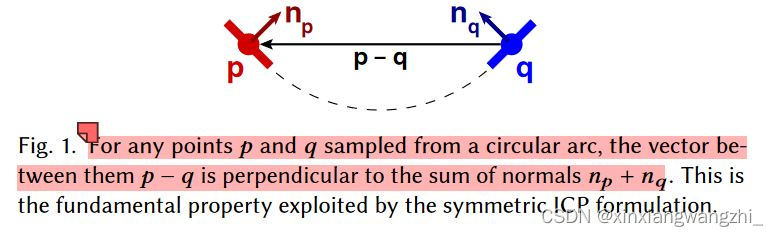
如图1所示，只要p,q位于圆弧上，此时向量（p-q）垂直于向量(np-nq)，等式4恒成立。

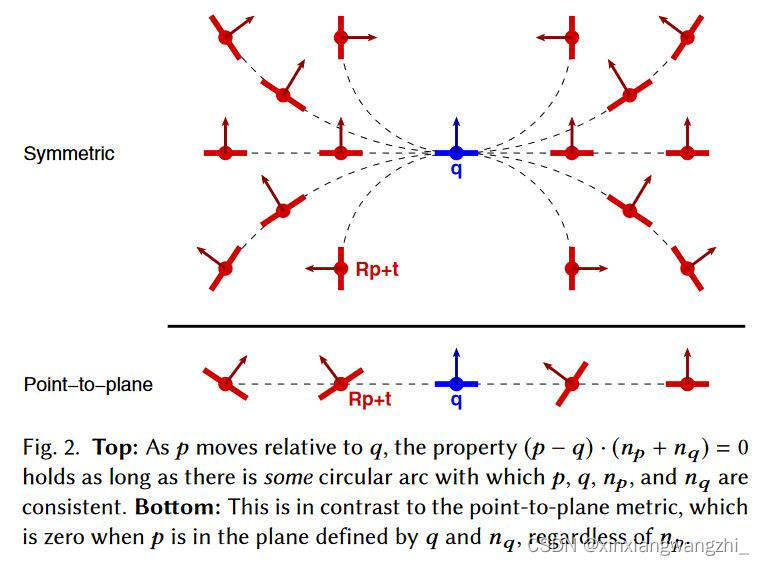
图2中，当 p 相对于 q 移动时，只要存在某个与 p、q、np 和 nq 一致的圆弧，性质 (p − q) · (np + nq ) = 0 就成立。点到面：当 p 位于 q 和 nq 定义的平面中时，无论 np 如何，点到平面度量为零。
对于等式4而言，在 3D 中也成立：只要 p 和 q 及其法线与某个圆柱体一致，方程 4 的计算结果就为零。
此外，4.1 节研究了一个不同的属性：只要 p 和 q 与位于它们之间的局部二阶曲面一致，方程 4 也成立。虽然此约束仍然为 (p, np ) 相对于 (q, nq ) 移动提供了更大的自由度，但它是比点到平面度量提供的“更有用”的自由形式。（增大了收敛域，更容易找到全局最优变换）。
对于目标函数而言，大多数先前的工作仅将刚体变换应用于其中一个表面（例如，点到面中的变换仅应用于 p），但我们考虑变换的对称形式：我们想象在一个固定的“中性”坐标中（既不在p坐标系也不在q坐标系中）评估度量，并对 P 和 Q 应用相反的变换。因此，我们可以将对称目标制定为：
$${\mathcal{E}}_{symm-RN}=\sum _i{\left[\left({\mathrm{R}}_i-{\mathrm{R}}^{-1}{q}_i+t\right)\cdot \left(\mathrm{R}{n}_{p,i}+{\mathrm{R}}^{-1}{n}_{q,i}\right)\right]}^2,\text{\hspace{1em}(5)}$$
我们还探索了该目标的一个更简单的版本，其中法线不旋转。也就是说，每个点对的最小化方向保持固定，而点本身沿相反方向旋转：
$${\mathcal{E}}_{symm}=\sum _i{\left[\left({\mathrm{R}}_i-{\mathrm{R}}^{-1}{q}_i+t\right)\cdot \left(n_{p,i}+n_{q,i}\right)\right]}^2\text{\hspace{1em}(6)}$$
为什么这是一个合理的简化？考虑二维中两个单位长度向量的总和。对向量应用相反的旋转可以保留它们的总和的方向，以便每个点对对目标的两个变体的贡献在一定程度上是相同的。在 3D 中，并非所有旋转轴都如此，但当 np 接近 nq 时，这一点也接近正确。 4.3 节中的实验表明，两个目标导致相似的收敛，但 Esymm 导致更简单的推导和实现。因此，本文的其余部分采用 Esymm 作为对称目标。

线性化

我们从 Rodrigues 旋转公式开始的线性化，以了解旋转 R 对向量 v 的影响：
$$\mathrm{R}v=v\cos \theta +(a\times v)\sin \theta +a(a\cdot v)(1-\cos \theta )\text{\hspace{1em}(7)}$$
其中 a 和 θ 是旋转轴和角度。我们观察到，(7) 中的最后一项与增量旋转角 θ 成二次方，因此我们将其丢弃以进行线性化：
$$\begin{array}{rl}\mathrm{R}v& \approx v\cos \theta +(a\times v)\sin \theta \\ & =\cos \theta (v+(\tilde{a}\times v)),\end{array}\text{\hspace{1em}(8)}$$

where $\tilde{a}=a\tan \theta$. Substituting into (6),
$$\begin{array}{rl}{\mathcal{E}}_{\text{symm }}\approx & \sum _i[\cos \theta \left(p_i-q_i\right)\cdot n_i+\\ & {\cos \theta \left(\tilde{a}\times \left(p_i+q_i\right)\right)\cdot n_i+t\cdot n_i]}^2\\ =\sum _i{\cos }^2\theta & [\left(p_i-q_i\right)\cdot n_i+\\ & {\left(\left(p_i+q_i\right)\times n_i\right)\cdot \tilde{a}+n_i\cdot \tilde{t}]}^2,\end{array}\text{\hspace{1em}(9)}$$
其中$n_i=n_{p,i}+n_{q,i}$ and $\tilde{t}=t/\cos \theta$。现在，我们对目标进行额外的近似加权 1/cos2 θ ，对于较小的 θ ，该值接近 1。 为了数值稳定性进一步考虑归一化，等式9变为如下形式：
$$\sum _i{\left[\left({\tilde{p}}_i-{\tilde{q}}_i\right)\cdot n_i+\left(\left({\tilde{p}}_i+{\tilde{q}}_i\right)\times n_i\right)\cdot \tilde{a}+n_i\cdot \tilde{t}\right]}^2\text{\hspace{1em}(10)}$$
where ${\tilde{p}}_i=p_i-\bar{p}$ and ${\tilde{q}}_i=q_i-\bar{q}$. This is a least-squares problem in $\tilde{a}$ and $\tilde{t}$, and the final transformation from $\mathcal{P}$ to $Q$ is:
$$\mathrm{trans}(\bar{q})\circ \mathrm{rot}\left(\theta ,\frac{\tilde{a}}{\Vert \tilde{a}\Vert }\right)\circ \mathrm{trans}(\tilde{t}\cos \theta )\circ \mathrm{rot}\left(\theta ,\frac{\tilde{a}}{\Vert \tilde{a}\Vert }\right)\circ \mathrm{trans}(-\bar{p}),\text{\hspace{1em}(11)}$$
where $\theta ={\tan }^{-1}\Vert \tilde{a}\Vert$.
理论到此结束，后面我会对代码进行分析测试。