能对多条件依赖关系进行设计测试点---判定表法
等价类、边界值分析法主要关注单个输入类条件的测试
定义:是一种以表格形式表达多条件逻辑判断的工具。
条件桩: 列出问题中的所有条件,列出条件的次序无关紧要
动作桩: 列出问题中可能采取的操作,操作的排列顺序没有约束
条件项: 列出条件对应的取值,所有可能情况下的真假值
动作项: 列出条件项的、各种取值情况下应该采取的动作结果
判定表中贯穿条件项和动作项的一列就是一条规则
假设有n个条件,每个条件的取值有两个(0,1),全组合有2的n次方种规则
步骤:
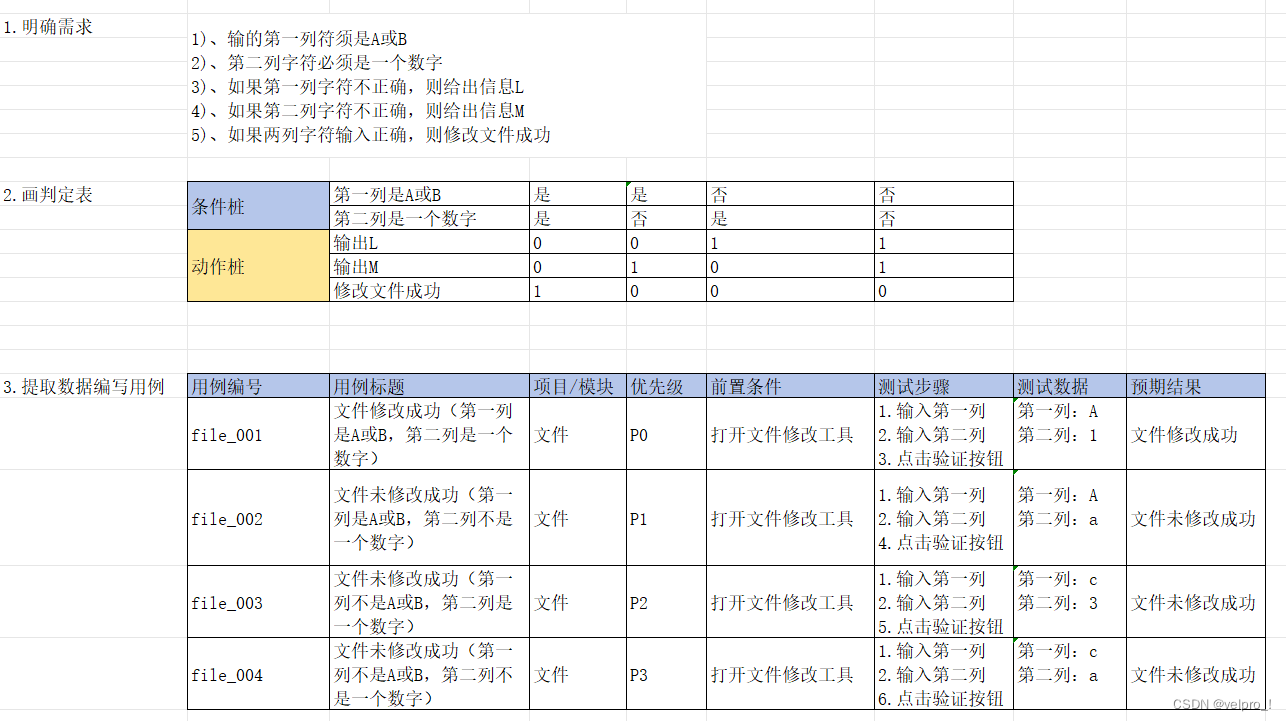
1.明确需求
2.画出判定表
1)列出条件桩和动作桩
2)填写条件项,对条件进行全组合
3)根据条件项的组合确定动作项
4)简化、合并相似规则
3.根据规则编写测试用例
案例1:
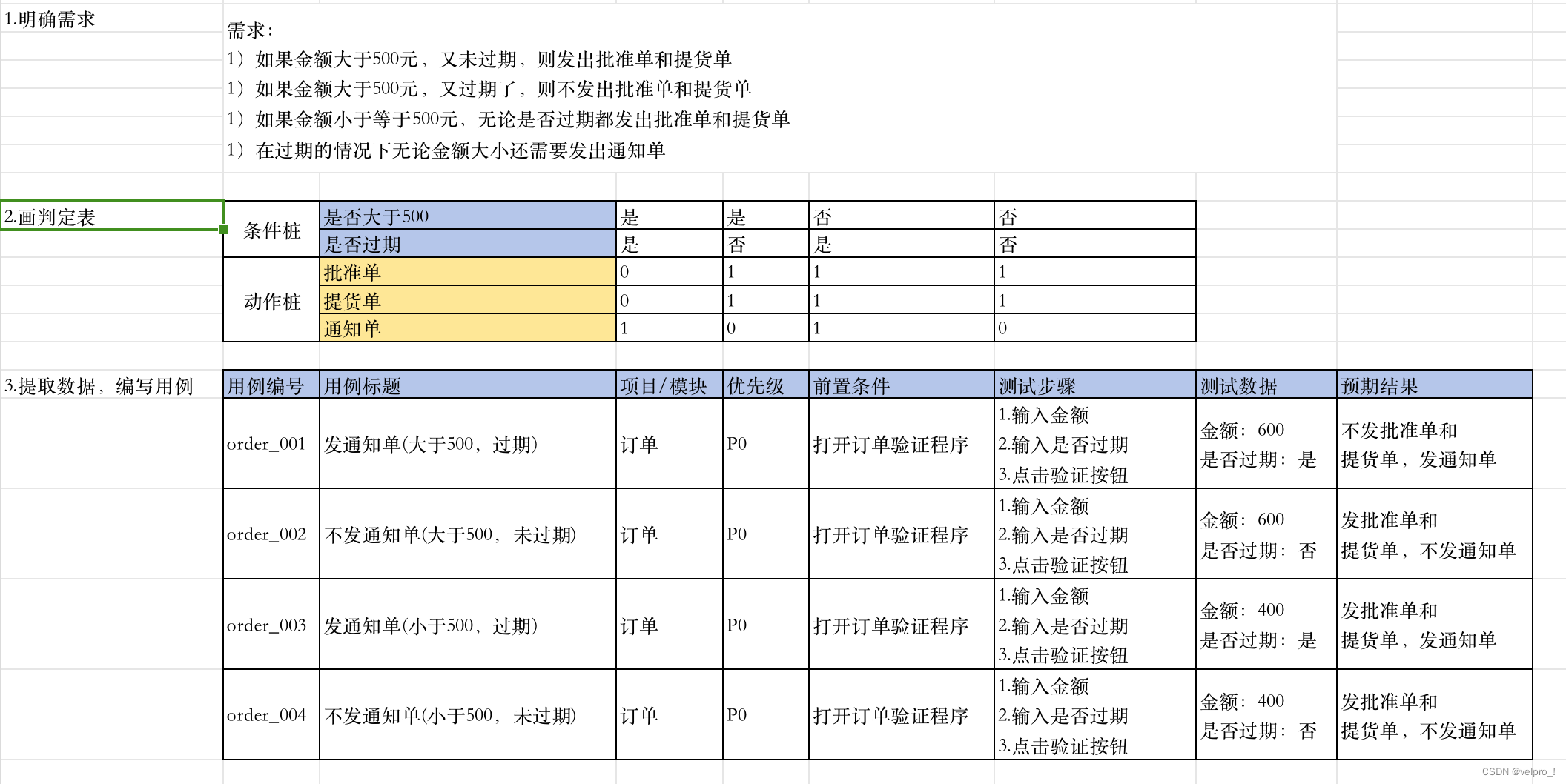
案例2:
使用场景:
1. 有多个输入条件,多个输出结果,输入条件之间有组合关系,输入条件和输出结果之间有依赖(制约)关系
2. 判定表一般适用于条件组合数量较少的情况(比如4不条件以下)
3. 如果条件超过4个,就不适合覆盖所有条件,应采用 (正交法) 来解决