二叉树经典算法题目

1.二叉树的前中后序遍历（简单）

省略

2.二叉树的深度(简单)

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

思路：递归，当前数的深度等于左子数和右子树其中最大深度再加1

代码：

class Solution {
    public int maxDepth(TreeNode root) {
       if (root==null){
           return 0;
       }
       return Math.max(maxDepth(root.right)+1,maxDepth(root.left)+1);
    }
}

3.层序遍历的应用

层序遍历思路：

使用一个队列，最开始先把root放进队列，然后弹出，打印，把左右子节点放入队列，周而复始，直到队列为空。

代码：

class Solution {
    public void levelOrder(TreeNode root) {
		 LinkedList<TreeNode> quene = new LinkedList();
         while(quene.size() != 0) {
            TreeNode value = quene.poll();
             
  			// 打印操作
            //...
             
            if(value.left != null){
                quene.add(value.left);
            }

            if(value.right != null){
                quene.add(value.right);
            }
         }
        
    }
}

3.1 二叉树的层平均值（简单）

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

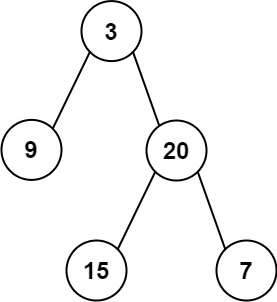
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

示例 2:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ILyhAOkc-1671953757561)(https://assets.leetcode.com/uploads/2021/03/09/avg2-tree.jpg)]

输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

提示：

树中节点数量在 [1, 104] 范围内
-231 <= Node.val <= 231 - 1

思路：套用层序遍历的模板，然后记录当前层的最后一个node,和下一层的最后一个node.(如果知道当前层的最后一个node是哪一个，在把node的左右节点发放入队列的时候，下一层的最后一个node就能得出)。然后就能够求每一层的平均值了。

代码：

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        LinkedList<TreeNode> quene = new LinkedList();
        List<Double> res = new ArrayList();
        TreeNode lastNode = root;  //当前层的最后一个node
        TreeNode nextLastNode = null;   //下一层的最后一个node
        int count = 0;
        long sum = 0;
        quene.add(root);


        // 层序遍历的应用
         while(quene.size() != 0) {

            TreeNode value = quene.poll();
   
            if(value.left != null){
                quene.add(value.left);
                nextLastNode = value.left;
            }

            if(value.right != null){
                quene.add(value.right);
                nextLastNode = value.right;
            }

            count++;
            sum += value.val;
            if(value == lastNode) {
                Double d = sum/(double)count;
                res.add(d);
                count = 0;
                sum = 0;
                lastNode = nextLastNode;
                nextLastNode = null;
            }

         }

        return res;
    }
}

3.2 二叉树最大宽度(中等)

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的宽度。

每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

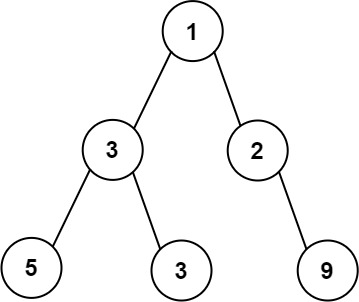
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

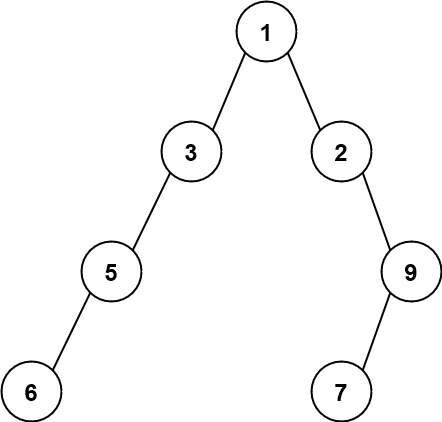
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

树中节点的数目范围是 [1, 3000]
-100 <= Node.val <= 100

思路：这一题的难点在于这些 null 节点也计入长度，而不是非空节点的宽度。

可以对节点进行编号。一个编号为 index，index 的左子节点的编号记为 2×index，右子节点的编号记为 2×index+1。直接对当前层最左边和最右边的节点相减再加1即可。和上一题的不同的一点是，还要知道当前层的第一个节点是谁。

代码：

class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        if(root == null) {
            return 0;
        }
        //层序遍历
        int max = 0;
        TreeNode lastNode = root;
        TreeNode firstNode = root;
        TreeNode nextLastNode = null;
        boolean firstFlag = false;

        LinkedList<TreeNode> stack = new LinkedList();
        HashMap<TreeNode,Integer> map = new HashMap();  //用于给节点编号
        stack.push(root);
        map.put(root,1);


        while(stack.size() != 0) {
            TreeNode node = stack.poll();
         
            if(!firstFlag){
                firstFlag = true;
                firstNode = node;
            }
           
            if(node.left != null) {
                stack.add(node.left);
                map.put(node.left,map.get(node)*2);  //给左子节点编号
                nextLastNode = node.left;
            }

            if(node.right != null) {
                stack.add(node.right);
                map.put(node.right,map.get(node)*2+1); //给右子节点编号
                nextLastNode = node.right;
            }

            if(node == lastNode) {
                max = Math.max(max,map.get(lastNode)-map.get(firstNode)+1);
                lastNode = nextLastNode;
                nextLastNode = null;
                firstFlag = false;
            }
        }
        return max;
    }

}

3.3 二叉树的完全性检验(中等)

给定一个二叉树的 root ，确定它是否是一个 完全二叉树 。

在一个 完全二叉树 中，除了最后一个关卡外，所有关卡都是完全被填满的，并且最后一个关卡中的所有节点都是尽可能靠左的。它可以包含 1 到 2h 节点之间的最后一级 h 。

示例 1：

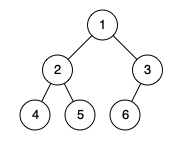
输入：root = [1,2,3,4,5,6]
输出：true
解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

示例 2：

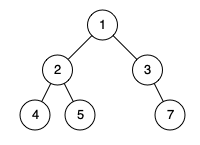
输入：root = [1,2,3,4,5,null,7]
输出：false
解释：值为 7 的结点没有尽可能靠向左侧。

提示：

树的结点数在范围 [1, 100] 内。
1 <= Node.val <= 1000

思路：层序遍历，对每一个节点进行检查。1.遇到左子节点为空，右子节点不为空的情况，不满足 2.遇到第一个左子节点不为空，右子节点为空或者在右子节点都为空的时候，下面的节点子节点均为叶。

代码：

class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        if(root == null) {
            return 0;
        }
        //层序遍历
        int max = 0;
        TreeNode lastNode = root;
        TreeNode firstNode = root;
        TreeNode nextLastNode = null;
        boolean firstFlag = false;

        LinkedList<TreeNode> stack = new LinkedList();
        HashMap<TreeNode,Integer> map = new HashMap();
        stack.push(root);
        map.put(root,1);


        while(stack.size() != 0) {
            TreeNode node = stack.poll();
         
            if(!firstFlag){
                firstFlag = true;
                firstNode = node;
            }
           
            if(node.left != null) {
                stack.add(node.left);
                map.put(node.left,map.get(node)*2);
                nextLastNode = node.left;
            }

            if(node.right != null) {
                stack.add(node.right);
                map.put(node.right,map.get(node)*2+1);
                nextLastNode = node.right;
            }

            if(node == lastNode) {
                max = Math.max(max,map.get(lastNode)-map.get(firstNode)+1);
                lastNode = nextLastNode;
                nextLastNode = null;
                firstFlag = false;
            }
        }
        return max;
    }
}

4. 验证二叉搜索树（中等）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

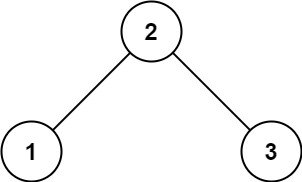
输入：root = [2,1,3]
输出：true

示例 2：

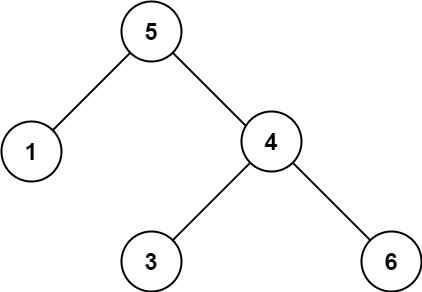
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

思路：左右子树是二叉搜索数，并且左子数的最大值应该小于当前值，右子数的最小值，应该大于当前值

代码：

class TreeRes {
    boolean flag;
    Integer min;
    Integer max;
    TreeRes(boolean flag, Integer min, Integer max) {
        this.flag = flag;
        this.min = min;
        this.max = max;
    }
} 

class Solution {
    public boolean isValidBST(TreeNode root) {
        if(root == null) {
            return true;
        }

        return isBST(root).flag; 
    }

    public TreeRes isBST(TreeNode root) {
        if(root == null) {
            return new TreeRes(true,null,null);
        }

        TreeRes leftRes = isBST(root.left);
        TreeRes rightRes = isBST(root.right);

        if((!leftRes.flag) || (!rightRes.flag)) {
            return new TreeRes(false,null,null);
        }

        if((leftRes.max != null && leftRes.max >= root.val) || (rightRes.min != null && rightRes.min <= root.val)) {
            return new TreeRes(false,null,null);
        }

        int min = leftRes.min != null ? leftRes.min : root.val;
        int max = rightRes.max != null ? rightRes.max : root.val;

        return new TreeRes(true,min,max);
    }
   
}