1.平衡二叉树的定义

平衡二叉树（Balanced Binary Tree），简称平衡树（AVL树）：树上任一结点的左子树和右子树的高度之差不超过1。
结点的平衡因子=右子树高-左子树高。
平衡二叉树结点的平衡因子的值只可能是−1、0或1。

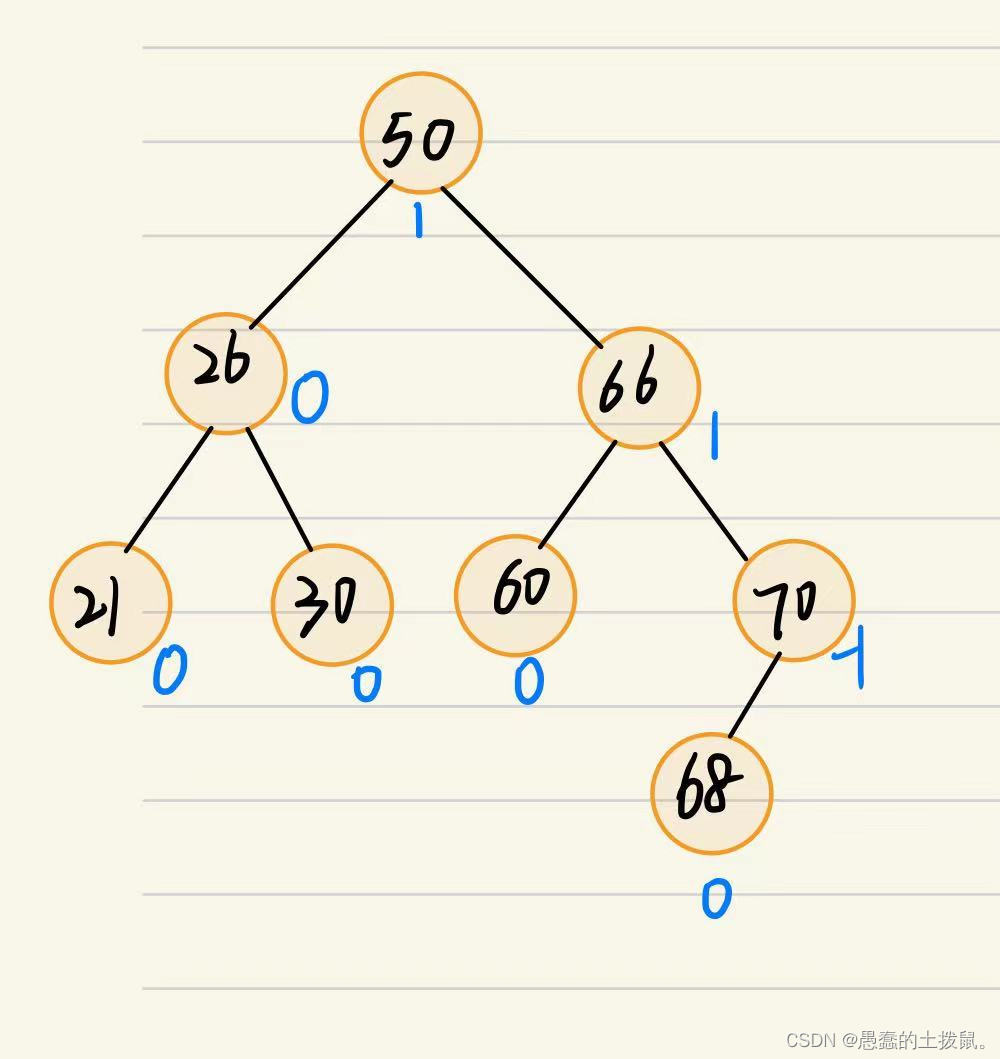
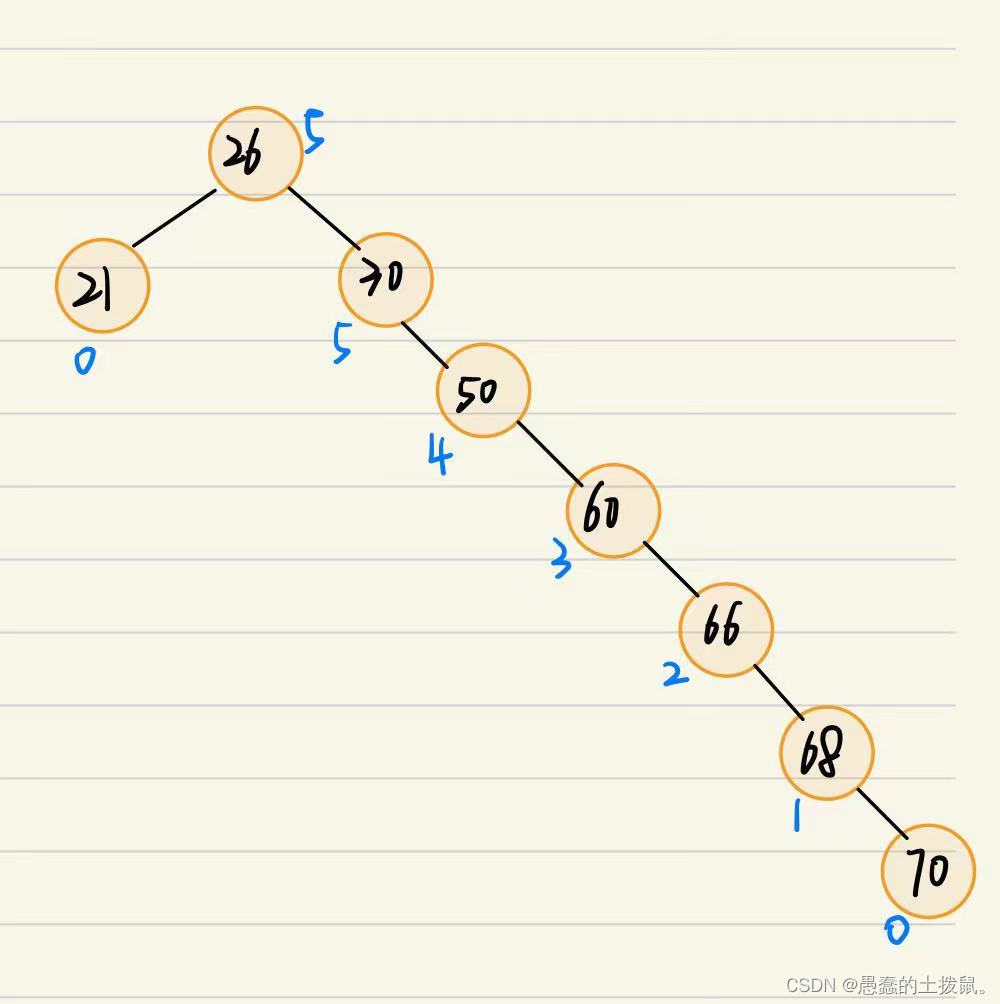
只要有任一结点的平衡因子绝对值大于1，就不是平衡二叉树。

2.平衡二叉树的插入（调整最小不平衡子树A）

在二叉排序树中插入新结点后，如何保持平衡？
查找路径上的所有结点都有可能受到影响。
从插入点往回找到第一个不平衡结点，调整以该结点为根的子树。
每次调整的对象都是“最小不平衡子树”

2.1LL（在A的左孩子的左子树中插入导致不平衡）

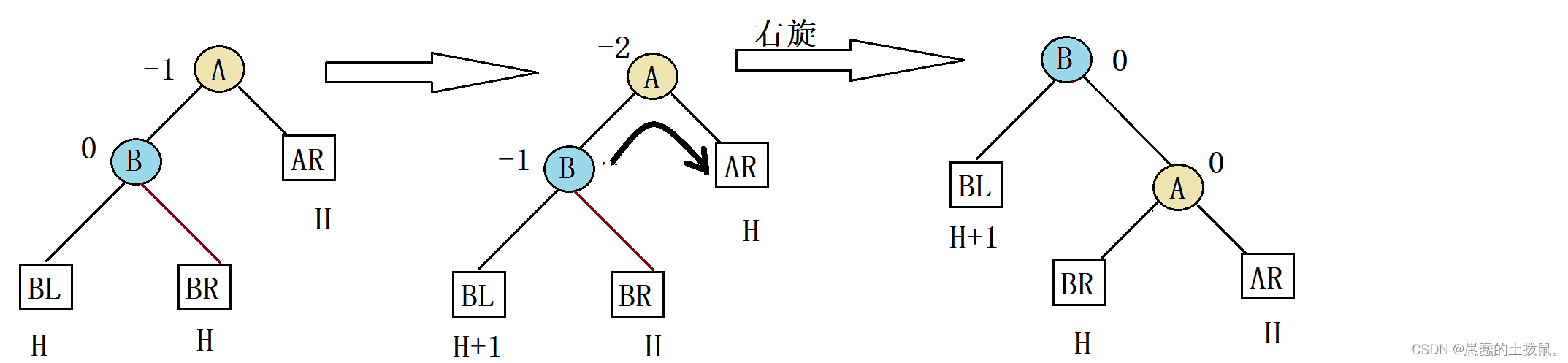
LL平衡旋转（右单旋转）。
由于在结点A的左孩子（L）的左子树（L）上插入了新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要一次向右的旋转操作。
总结为如下三步：
①newroot指向B
②A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树
③A的左孩子B向右上旋转代替A成为根结点

//右单旋转
AVLNode* AVLTree::RotateRight(AVLNode* ptr)
{
//1.
    AVLNode* newroot = ptr->leftchild;
    newroot->parent = ptr->parent;
//2.
    ptr->leftchild = newroot->rightchild;
    if (newroot->rightchild)
    {
        newroot->rightchild->parent = ptr;
    }
    newroot->rightchild = ptr;

    AVLNode* parent = ptr->parent;
    if (parent == nullptr)
    {
        root = newroot;
    }
    else
    {
        if (parent->leftchild == ptr)
        {
            parent->leftchild = newroot;
        }
        else
        {
            parent->rightchild = newroot;
        }
    }
//3.
    ptr->parent = newroot;

    return newroot;
}

2.2RR（在A的右孩子的左子树中插入导致不平衡）

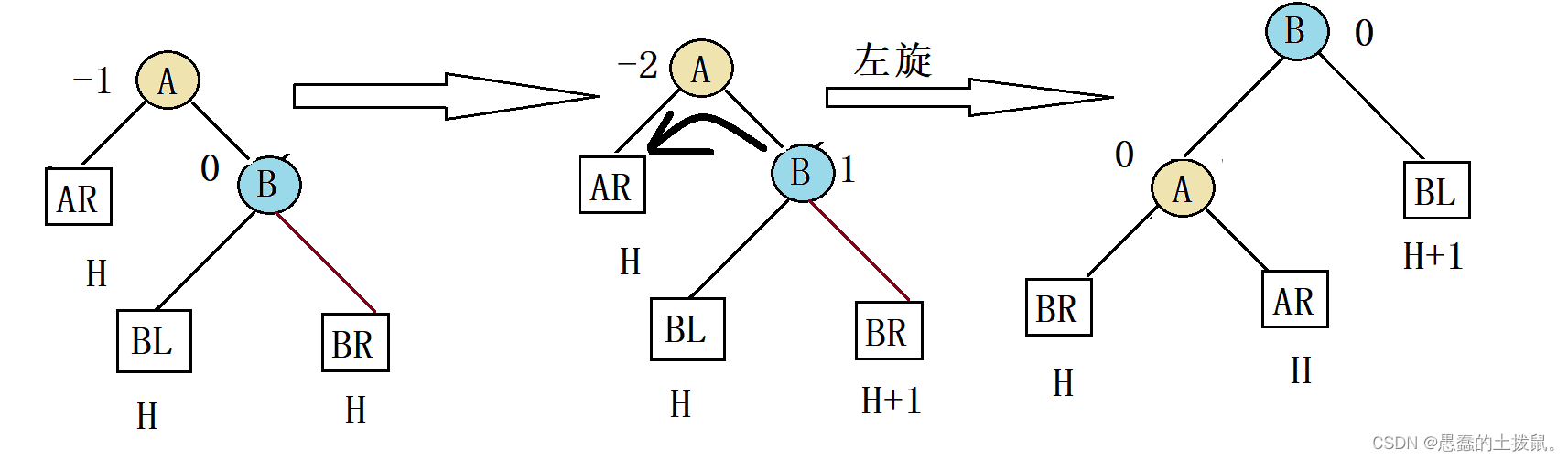
RR平衡旋转（左单旋转）。由于在结点A的右孩子（R）的右子树（R）上插入了新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要一次向左的旋转操作。
具体操作步骤总结如下：
①newroot指向B
②将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树
③将A的右孩子B向左上旋转代替A成为根结点，

//左单旋转
AVLNode* AVLTree::RotateLeft(AVLNode* ptr)
{
    //1.
    AVLNode* newroot = ptr->rightchild;
    newroot->parent = ptr->parent;

    //2.
    ptr->rightchild = newroot->leftchild;
    if (newroot->leftchild != nullptr)
    {
        newroot->leftchild->parent = ptr;
    }
    newroot->leftchild = ptr;

    //考虑ptr不为根的情况
    AVLNode* parent = ptr->parent;
    if (parent == nullptr)
    {
        root = newroot;
    }
    else
    {
        if (parent->leftchild == ptr)
        {
            parent->leftchild = newroot;
        }
        else
        {
            parent->rightchild = newroot;
        }
    }
    //3.
    ptr->parent = newroot;

    return newroot;
}

2.3LR（在A的左孩子的右子树中插入导致不平衡）

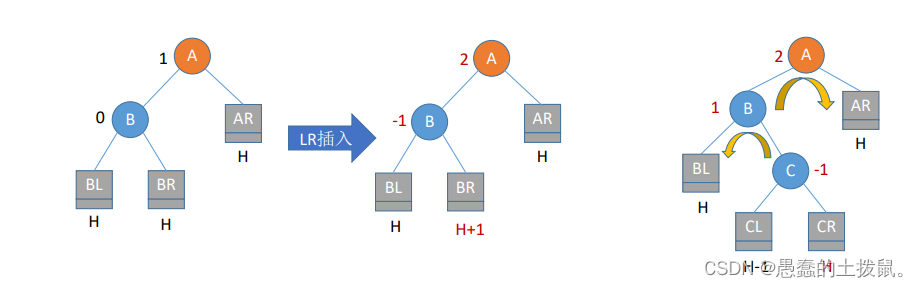
LR平衡旋转（先左后右双旋转）。由于在A的左孩子（L）的右子树（R）上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置。

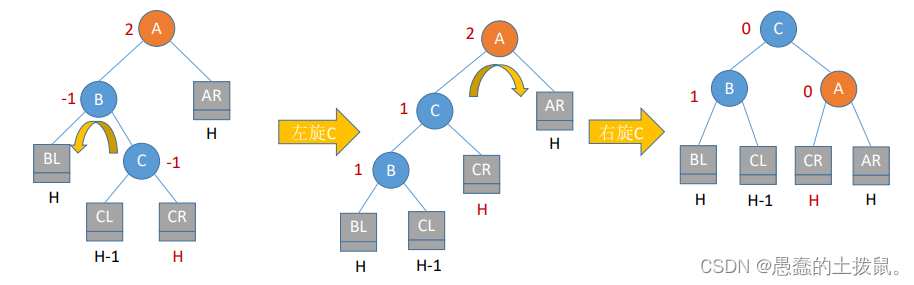
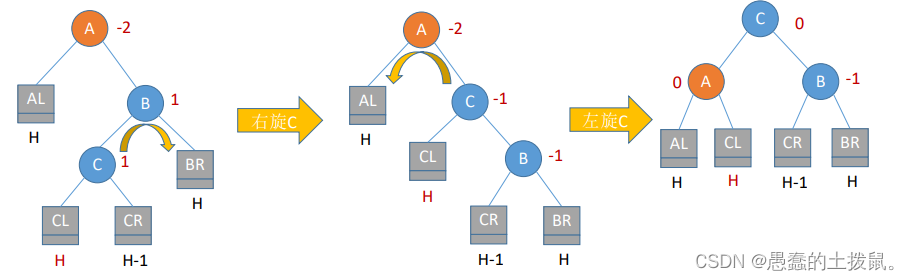
2.4RL（在A的右孩子的左子树中插入导致不平衡）

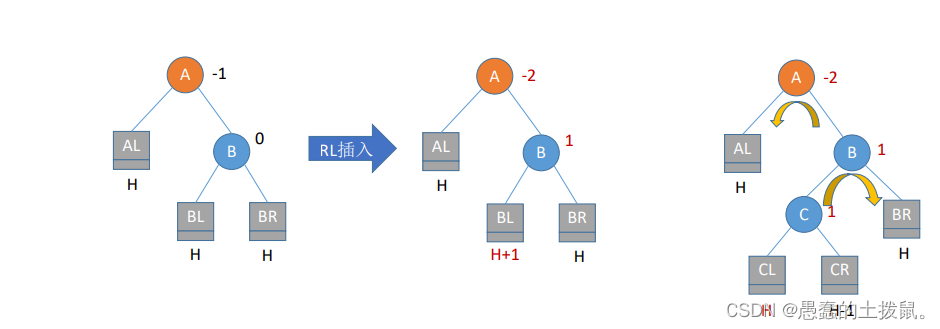
RL平衡旋转（先右后左双旋转）。由于在A的右孩子（R）的左子树（L）上插入新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置。

3.平衡二叉树的所有操作代码

平衡二叉树代码