第19章 随机变量
19.1随机变量示例
定义19.1.1:概率空间上的随机变量R是域等于样本空间的全函数。
R的陪域可以是任何东西,但通常是实数的一个子集。
例:
例如,假设我们抛三个独立的、公平的硬币。令C表示正面朝上的次数。如果三个硬币全都是正面或者全都是反面朝上,则令M= 1;否则,M = 0。那么,三个硬币抛掷的每一个结果唯一确定C和M的值。
那么,C是将样本空间中的每个结果映射成数值的函数,即:
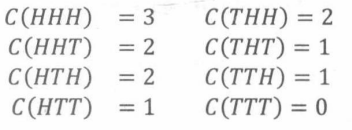
同理,M是将样本空间中的每个结果按另一种方式映射的函数,如下:
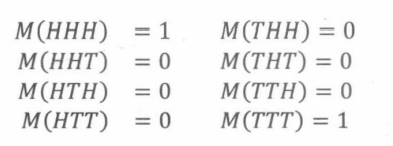
所以,M和C是随机变量。
19.1.1 指示器随机变量
指示器随机变量是将每个结果映射成0或1的随机变量。指示器随机变量又称伯努利变量。上文提到的随机变量M就是指示器随机变量。如果抛出的三个硬币的面相同,则M=1,否则M=0。
同样地,事件E将样本空间划分为:属于E的结果,以及不属于E的结果。所以,事件E天然带有一个相应的指示器随机变量 I E I_E IE:若结果w ∈ E,则 I E I_E IE(w)=1;若 w ∉ E w\notin E w∈/E,则 I E I_E IE(w)= 0。因此,M= I E I_E IE,其中E表示事件“三个硬币抛的面相同”。
19.1.2 随机变量和事件
事件和一般的随机变量之间也存在着密切的联系。一个随机变量有几个值,就能将样本空间分为几个块。例如,C将样本空间划分为:

每一个块对应样本空间的一个子集,因此是一个事件。
一般来说,任意关于随机变量取值的断言( assertion)都定义了一个事件。
19.2独立性
独立性 ( independence)既可以用于描述事件又可以用于描述变量。随机变量 R 1 R_1 R1和 R 2 R_2 R2是独立的,当且仅当以下两个事件

对于所有的x1,x2是独立的。
引理19.2.1 两个事件独立,当且仅当这两个事件的指示器变量是独立的。
从直觉上来说,两个随机变量独立,意味着知道一个变量的某些信息,对另一个变量没有任何帮助。一个变量R的“某些信息”是指与R有关的某个数值。而且,这种独立的特性意味着独立变量的函数也是相互独立的。
引理19.2.2:设R和S是两个独立的随机变量,f和g是两个函数,其中域(f)=陪域®且域(g)=陪域(S)。那么,f®和g(S)是独立随机变量。
定义19.2.3:随机变量 R 1 , R 2 … , R n R_1,R_2…,R_n R1,R2…,Rn是相互独立的当且仅当对于所有的 X 1 , X 2 , … , X n X_1,X_2,… ,X_n X1,X2,…,Xn,n个事件

是相互独立的。它们是k-次独立的当且仅当它们的任意k元素子集是相互独立的。
19.3 分布函数
随机变量将结果映射为数值。随机变量R的概率密度函数 P D F R ( x ) PDF_R(x) PDFR(x)衡量了R取值为x的概率,以及密切相关的累积分布函数 C D F R ( x ) CDF_R(x) CDFR(x)衡量了R ≤ X的概率。不同结果空间的随机变量常常具有相似的表现形式,是因为它们不同取值的概率相同,也就是说,它们具有相同的PDF/CDF。
定义19.3.1:设R是一个随机变量,陪域为V。R的概率密度函数为PDFR:V→[0,1],定义如下:
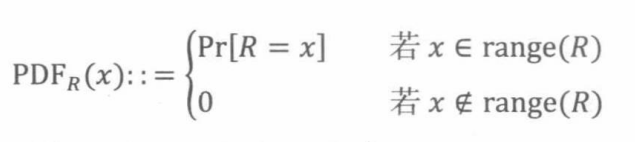
如果陪域是实数的子集,那么累积分布函数为 C D F R : R → [ 0 , 1 ] CDF_R:R→[0,1] CDFR:R→[0,1],定义如下:

由此可以推导出:

PDF;和CDF,都能提供关于R的信息,任君挑选。关键的一点是,无论是概率密度函数还是累积分布函数,都不涉及实验的样本空间。
事实上,有些PDF非常常见,所以都有特别的名字。例如,在计算机科学领域,有三个最重要的分布:伯努利分布、均匀分布和二项分布。接下来,我们仔细探讨一下这些分布。
19.3.1 伯努利分布
伯努利分布是伯努利变量的分布函数。具体来说,伯努利分布的概率密度函数的形式为fp:{0,1} →[0,1],其中

其中 p ∈ [ 0 , 1 ] p \in [0,1] p∈[0,1]。相应的累积分布函数为Fp:R→[0,1],其中:

19.3.2均匀分布
如果随机变量以相等的概率、取值为陪域中任意一个可能的值,则这个随机变量是均匀的。若陪域V有n个元素,那么均匀分布的概率密度函数的形式为:

其中:
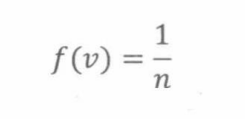
对所有v∈V成立。
如果V的元素按递增顺序依次为 a 1 , a 2 , … , a n a_1, a_2,… , a_n a1,a2,…,an,那么累积分布函数为F:R→ [0,1],其中:

19.3.3数字游戏
让我们来玩个游戏吧!有两个信封,每个信封里写有一个范围在0,1,…,100之间的整数,而且两个信封中的数字不同。如果猜出哪一个信封中的数字更大,那么你就赢了。为了给你一点机会,我们允许你任意选择一个信封,看一下信封中的数字。这样的话,有没有一种策略,使你赢得游戏的概率大于50%呢?
制胜策略分析
一般地,假设从整数区间[0…n]中挑选两个数。我们把较小的数称为L,把较大的数称为H。
你的目标是猜一个在L和H中间的数值x。选完x以后,你看到一个信封里的数字,设这个数字为T。如果T > x,那么你猜你看到的这个数字是比较大的。如果T<x,那么你猜另一个信封中的数字比较
接下来就是确定这个策略获胜的概率。我们采用四步法和树状图。
第一步:找到样本空间
你选择的x可能过小(<L)、过大(>H),或者刚刚好(L<x<H)。然后你选择看的那个数字可能是偏小(T=L)或偏大(T=H)的数字。所以,共有六种可能的结果,如图19.3所示。

第二步:定义目标事件
获胜事件的四种结果已经标记在树状图中。
第三步:计算结果的概率
首先,计算边的概率。x过小的概率是L/n,过大的概率是(n-H)/n,刚刚好的概率是(H - L)/n。然后,你选择看的这个信封是大数还是小数的概率是一样的。将根到叶子路径上的概率相乘,就得到了结果的概率。
第四步:计算事件的概率
将获胜事件的四种结果的概率相加,就是你在这个游戏中的胜率。

由于大数H至少比小数L大1且它们不相等,所以最后的不等式成立。
19.3.4 二项分布
计算机科学领域中最常用的第三个分布是二项分布。
服从二项分布的随机变量,最有代表性的例子就是n次独立抛硬币结果正面朝上的次数。如果硬币是均匀的,那么正面朝上的次数服从无偏二项分布,概率密度函数为 f n : [ 0.. n ] → [ 0 , 1 ] f_n:[0..n] →[0,1] fn:[0..n]→[0,1]

这是因为n次抛硬币正好有k次正面朝上的序列有 ( n k ) \binom{n}{k} (kn)种,而且每个序列的概率是 2 − n 2^{-n} 2−n。
广义二项分布
如果硬币是有偏好的,每一次抛到正面的概率是p,那么抛得正面的次数有一个广义二项分布密度函数,概率密度函数为 f n , p : [ 0.. n ] → [ 0 , 1 ] f_{n,p}:[0..n]→[0,1] fn,p:[0..n]→[0,1]
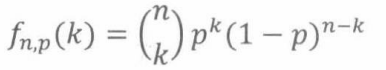
其中 n ∈ N + n ∈ N^+ n∈N+,p ∈ [0,1]。k个正面、 n - k个反面的序列有 ( n k ) \binom{n}{k} (kn)个,每一个序列的概率是 p k ( 1 − p ) n − k p^k(1-p)^{n-k} pk(1−p)n−k。
19.4 期望
随机变量的期望或期望值,是指能够揭示这个变量很多行为的单个数字。随机变量的期望又称均值或平均数。
定义19.4.1:如果R是定义在样本空间S的随机变量,那么R的期望是:
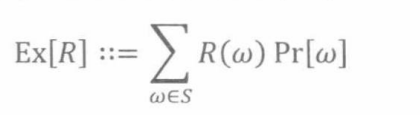
19.4.1 均匀随机变量的期望值
一般来说,如果R,是均匀分布在 a 1 , a 2 , … , a n {a_1 ,a_2,… , a_n} a1,a2,…,an上的随机变量,那么 R n R_n Rn的期望就是 a i a_i ai的平均值:
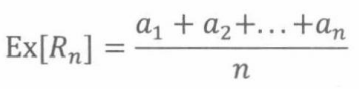
19.4.2随机变量的倒数的期望
定义随机变量S为一个公平的六面骰子抛出的点数的倒数。也就是说S = 1/R,其中R是抛出的点数。那么,
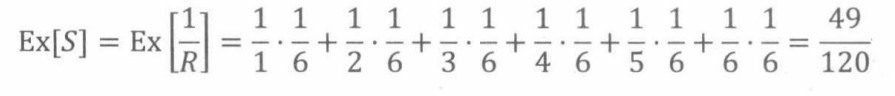
注意:

19.4.3 指示器随机变量的期望值
一个事件的指示器随机变量的期望值就是这个事件的概率。
引理19.4.2:如果IA是事件A的指示器随机变量,那么

19.4.4期望的另一种定义
还有另一种定义期望的标准方法。
定理19.4.3 对任意的随机变量R,
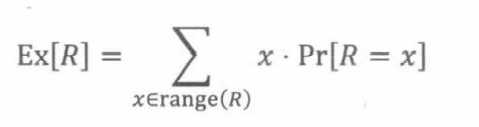
证明.设R定义在样本空间S中,那么

19.4.5 条件期望
正如事件概率一样,期望也可以以某个事件为条件。对于随机变量R,给定事件A的条件下,R的期望值等于它在事件A结果上的概率加权平均。即,
定义19.4.4 给定事件A的条件下,随机变量R的条件期望Ex[R|A]是:

定理19.4.5(全期望定理)设R是样本空间S上的一个随机变量,并且 A 1 , A 2 , … A_1,A_2,… A1,A2,…是S的划分,那么

证明:

19.4.6平均故障时间
如果一个计算机程序还没崩溃,那么它每小时崩溃的概率是p。那么程序崩溃所需的期望时间是多少? 假设C是直到程序第一次崩溃的小时数,我们要求Ex[C]。
定义A为系统在第一个小时崩溃的事件,则 A ‾ \overline{A} A为第一个小时系统没有崩溃的事件。那么平均故障时间Ex[C]为

由于A表示第一个小时系统崩溃,故:

由于 A ‾ \overline{A} A是第一个小时系统没有崩溃,所以以 A ‾ \overline{A} A为条件,相当于第一个小时系统不崩溃,接着在没有条件的情况下重新开始。因此
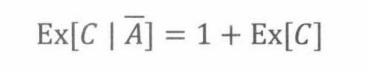
故:

平均故障时间:
假设系统在各个时间周期内独立运行,如果系统在每一个时间周期发生故障的概率是p,那么系统第一次出现故障所需的时间期望是1/p。
定义19.4.6 随机变量C服从参数为p的几何分布,当且仅当陪域©= Z+且

引理19.4.7 如果随机变量C服从参数为p的几何分布,那么
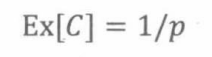
19.4.7赌博游戏的预期收益
预期收益等于0的游戏,被称为公平游戏。
我们再来看一个公平游戏。
你和其他两名玩家玩游戏,每个玩家拿出2美元放在吧台,然后各自悄悄在纸巾上写“正”或“反”。接着,抛一枚公平的硬币。猜对硬币结果的人平分吧台上的6美元。
用四步法则和树状图计算一下预期收益。树状图如图19.6所示。

根据式19.3计算期望收益:
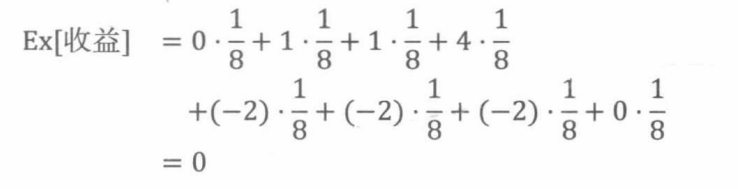
这说明这个游戏是公平的。
共谋的影响
如果另外两个人协商好,他们每次都选择不同的结果,你的期望收益会是多少呢?树状图如下

使用式19.3计算串谋情况下的期望收益,有:
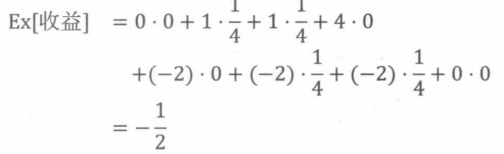
19.5期望的线性性质
期望遵循一个简单、有用的法则,称为期望的线性性质。简单地说:就是随机变量和的期望等于随机变量期望的和。
定理19.5.1 对任意随机变量R1和R2,有:
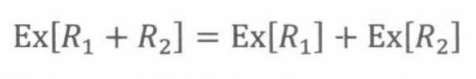
定理19.5.2 对于随机变量R1,R2和常数a1,a2 ∈ R,有
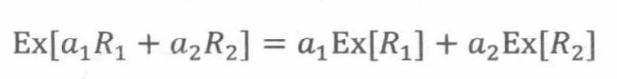
也就是说,期望是一个线性函数。将以上定理拓展至两个以上变量的情况,可得
推论19.5.3(期望的线性性质),对任意随机变量R1,…,Rg和常数a1
… , ax ∈R,有
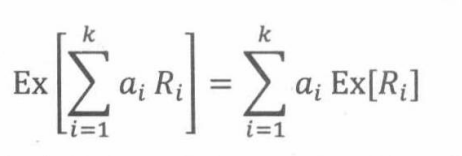
19.5.1 两枚骰子的期望
两枚公平骰子抛出的点数和的期望是多少?
设随机变量 R 1 R_1 R1是第一枚骰子抛出的点数, R 2 R_2 R2是第二枚骰子抛出的点数。根据前面的计算我们知道,一枚骰子的期望值是3.5。使用期望的线性性质可得两枚骰子和的期望:
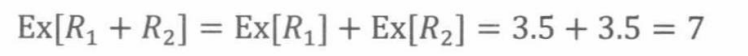
注意:不需要假设两个骰子是独立的。即使它们以某种可控的方式共同产生抛掷结果,只要这两个骰子都是公平的,那么它们的和的期望值就等于7。
19.5.2 指示器随机变量的和
期望的线性性质尤其适合指标器随机变量的和。举一个例子,假设有一个晚餐派对, n个男人检查他们的帽子。在就餐期间,帽子混在一起,随后每个人都会随机地得到一顶帽子。每个人以概率1/n拿到自己的帽子。请问能够正确拿到自己帽子的人有多少个?
将G表示为指示器随机变量的和。特别地,令 G i G_i Gi表示事件“第i个人拿到自己帽子”的指示器随机变量。也就是说,如果第i个人得到自己的帽子,则 G i G_i Gi=1,否则 G i G_i Gi=0。那么得到自己的帽子的人数就是这些指示器随机变量的和:

这些指示器随机变量不是相互独立的。这里我们再强调一遍,不必考虑这些变量是否独立,期望的线性性质总是成立的。
由于 G i G_i Gi是一个指示器随机变量,我们从引理19.4.2可以得出

所以
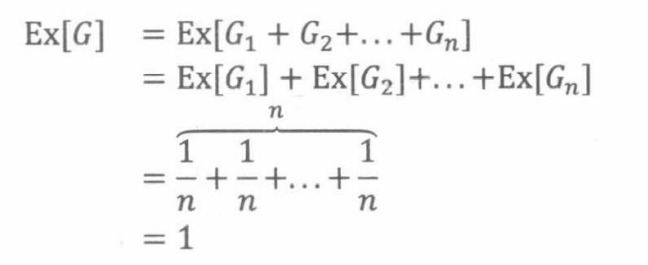
定理19.5.4:给定任意一系列事件A1,A-,… ,An,将要发生的事件数目的期望是

19.5.3二项分布的期望
假设独立地抛n个有偏好的硬币,每个硬币正面朝上的概率是p。那么正面朝上次数的期望是多少?

根据式19.3,这意味着
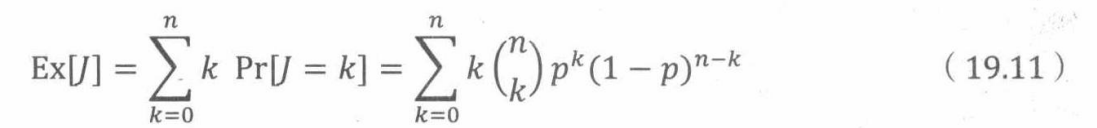
我们可以用期望的线性性质可以推导出一个简单闭型。
J i J_i Ji表示第i个硬币正面朝上的指示器随机变量,即

那么正面向上的次数就是

由定理19.5.4

19.5.4 赠券收集问题
有多个颜色的火箭车。我们在点餐的时候得到的汽车颜色是随机且独立的。要想每种颜色的火箭车至少有一个,需要购买儿童套餐个数的期望是多少?
当有k种颜色的时候,每份儿童套餐附赠的车是我们已经有的颜色的概率是k/n。那么,每份套餐附赠新颜色的概率是1- k/n = (n -k)/n。因此,根据平均故障时间法则,一直买直到得到新颜色,所需套餐数量的预期是n/(n -k)。这意味着

结合期望的线性性质,我们可以解决赠券收集问题:
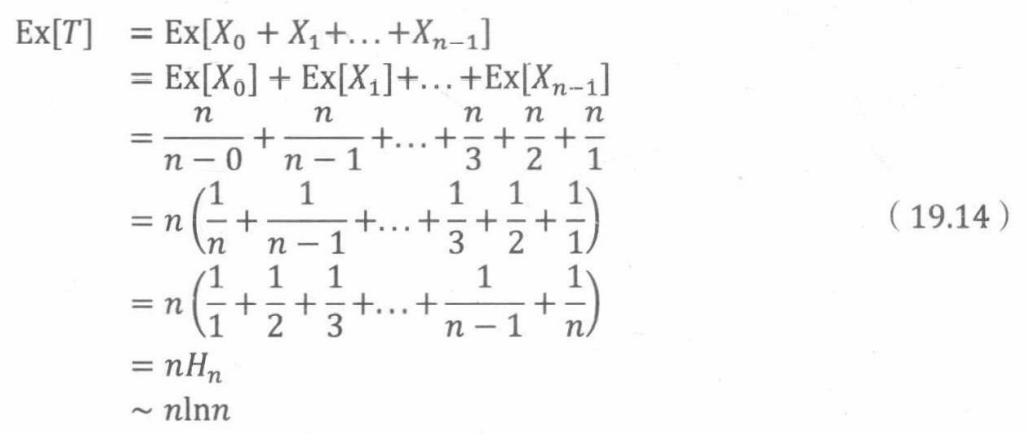
19.5.5 无限和
只要变量满足绝对收敛标准准则,期望的线性性质就同样适用于无限个随机变量的情况。
定理19.5.5(期望的线性性质)设 R 0 , R 1 R_0,R_1 R0,R1,…为随机变量,且有

收敛,则

19.5.6赌博悖论
在美国,有一个名为轮盘赌轮的游戏。有18个黑色槽、18个红色槽、2个绿色槽,你可以压黑色或者红色。如果你压了10美元,并且压对了,你就可以10美元本金和10美元奖金。出现红色或者黑色的概率是18/38 ≈ 0.473。
当然,即使你有幸用一个概率为0.5的公平轮盘赌博,也不一定就能赢钱。假设使用公平轮盘,你每次下注赢和输的概率是一样的,所以每转一次期望收益是零。因此,继续下注,每一局期望收益的和仍然是零。
尽管如此,赌徒也会尝试不同的投注策略,以赢得轮盘赌。一个著名的策略是押注加倍( betdoubling ),比如下注10美元、红色,然后不断加倍,直到红色出现为止。这意味着如果第一次就转出红色,那么停止下注,赢得10美元并离开赌场。如果没有出现红色,第二次继续下注20美元。如果第二次转出红色,则得到20美元的本金加上20美元的回报,然后离开,净利润为20-10= 10美元。如果第二次还没有出现红色,继续下注40美元,如果第三次转出红色则离开,此时净利润是40一20 -10= 10美元,以此类推。
前面我们已经分析过公平轮盘赌根本赢不了钱,但这对不公平的轮盘赌不适用。
19.5.7悖论的解答
“公平轮盘赌的期望收益是零”这一论断的错误之处在于,含蓄地误用了无限和的期望的线性性质。
这里的问题在于,赢钱的绝对值的和的期望是发散的,不满足无限线性的条件。在押注加倍的情况下,第n次下注 10 ⋅ 2 n − 1 10·2^{n-1} 10⋅2n−1美元,而赌局能进行到第n局的概率是 2 − n 2^{-n} 2−n所以

因此,和
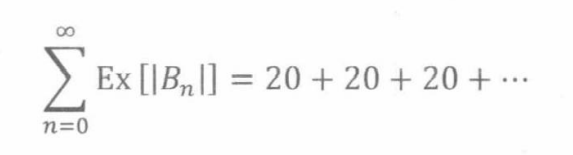
迅速发散。
19.5.8乘积的期望
期望的和就是和的期望,但是乘积往往不具备这样的性质。
但是,有一种特殊情形,乘积的期望等于期望的乘积。那就是当乘积中的随机变量相互独立的时候。
定理19.5.6 对任意两个独立的随机变量
R
1
,
R
2
R_1, R_2
R1,R2,
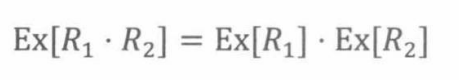
这个定理的证明方法是对定义
E
x
[
R
1
]
⋅
E
x
[
R
2
]
Ex[R_1]·Ex[R_2]
Ex[R1]⋅Ex[R2]的和式进行重新组合。
定理19.5.6可以直接推广到多个相互独立的变量。
推论19.5.7:[独立乘积的期望]如果随机变量 R 1 , R 2 , . . . . . . R 3 R_1,R_2,...... R_3 R1,R2,......R3是相互独立的,那么