目录

​​​​​​​一：股票预测数据分析

二：K线图数据分析

---

​​​​​​​一：股票预测数据分析

1-1 导入需要使用到的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

1-2 读取csv数据

data = pd.read_csv("stock.csv", encoding='gbk')
print(data.head())

          日期     股票代码    名称  ...         成交金额           总市值          流通市值
0  2021/3/15      '600519  贵州茅台  ...         12459955712  2.480000e+12  2.480000e+12
1  2021/3/12      '600519  贵州茅台  ...         8181594631  2.550000e+12  2.550000e+12
2  2021/3/11      '600519  贵州茅台  ...         11521736384  2.570000e+12  2.570000e+12
3  2021/3/10      '600519  贵州茅台  ...         10136910284  2.470000e+12  2.470000e+12
4  2021/3/9       '600519  贵州茅台  ...         16100769579  2.430000e+12  2.430000e+12

[5 rows x 15 columns]

1-3 空值处理

# Index(['收盘价', '最高价', '最低价', '开盘价', '前收盘', '涨跌额', '涨跌幅', '换手率', '成交量', '成交金额','成交量', '流通市值'],
# 删除不需要的列
data.drop(['股票代码', '名称', '日期', ], axis=1, inplace=True)  # 删除操作  # '涨跌额','涨跌幅','成交金额','总市值','流通市值','成交量','换手率'
# 空值所在行删除
data = data.dropna(axis=0, how='any')
print(data.head())
print(data.columns)  # 打印表头

       收盘价      最高价      最低价  ...         成交金额           总市值          流通市值
0      1975.45  2069.80  1951.15  ...  12459955712  2.480000e+12  2.480000e+12
1      2026.00  2077.00  2002.01  ...   8181594631  2.550000e+12  2.550000e+12
2      2048.00  2079.99  1961.48  ...  11521736384  2.570000e+12  2.570000e+12
3      1970.01  1999.87  1967.00  ...  10136910284  2.470000e+12  2.470000e+12
4      1936.99  2000.00  1900.18  ...  16100769579  2.430000e+12  2.430000e+12

[5 rows x 12 columns]
Index(['收盘价', '最高价', '最低价', '开盘价', '前收盘', '涨跌额', '涨跌幅', '换手率', '成交量', '成交金额',
       '总市值', '流通市值'],
      dtype='object')

1-4 两类相关性分析

1-4-1 收盘价 前收盘

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("收盘价和前收盘相关性图")
plt.xlabel('收盘价', fontsize=8)
plt.ylabel('前收盘', fontsize=8)
plt.scatter(data["收盘价"].values, data["前收盘"].values)
plt.show()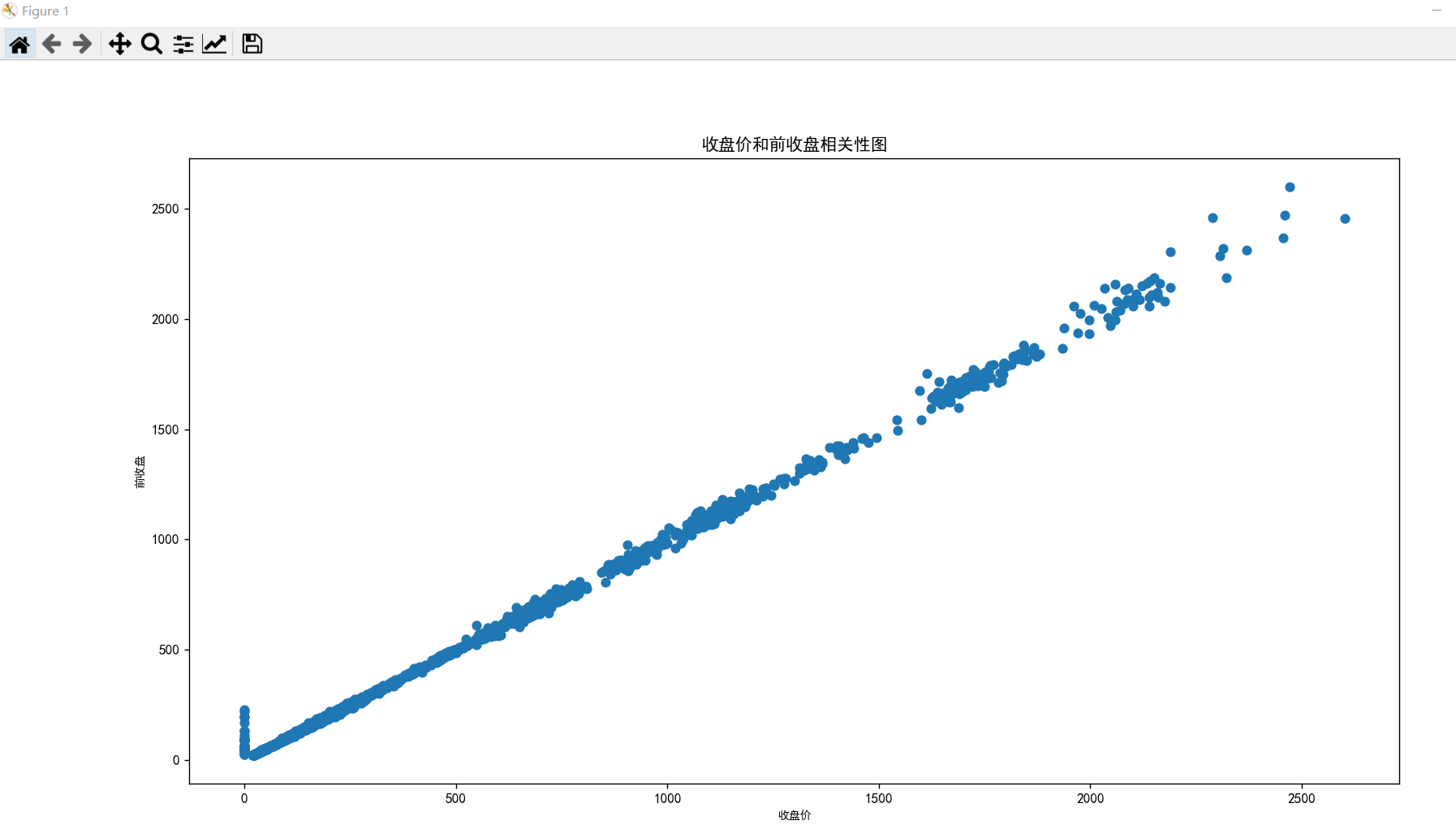

1-4-2 收盘价 开盘价

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("收盘价和开盘价相关性图")
plt.xlabel('收盘价', fontsize=8)
plt.ylabel('开盘价', fontsize=8)
plt.scatter(data["收盘价"].values, data["开盘价"].values)
plt.show()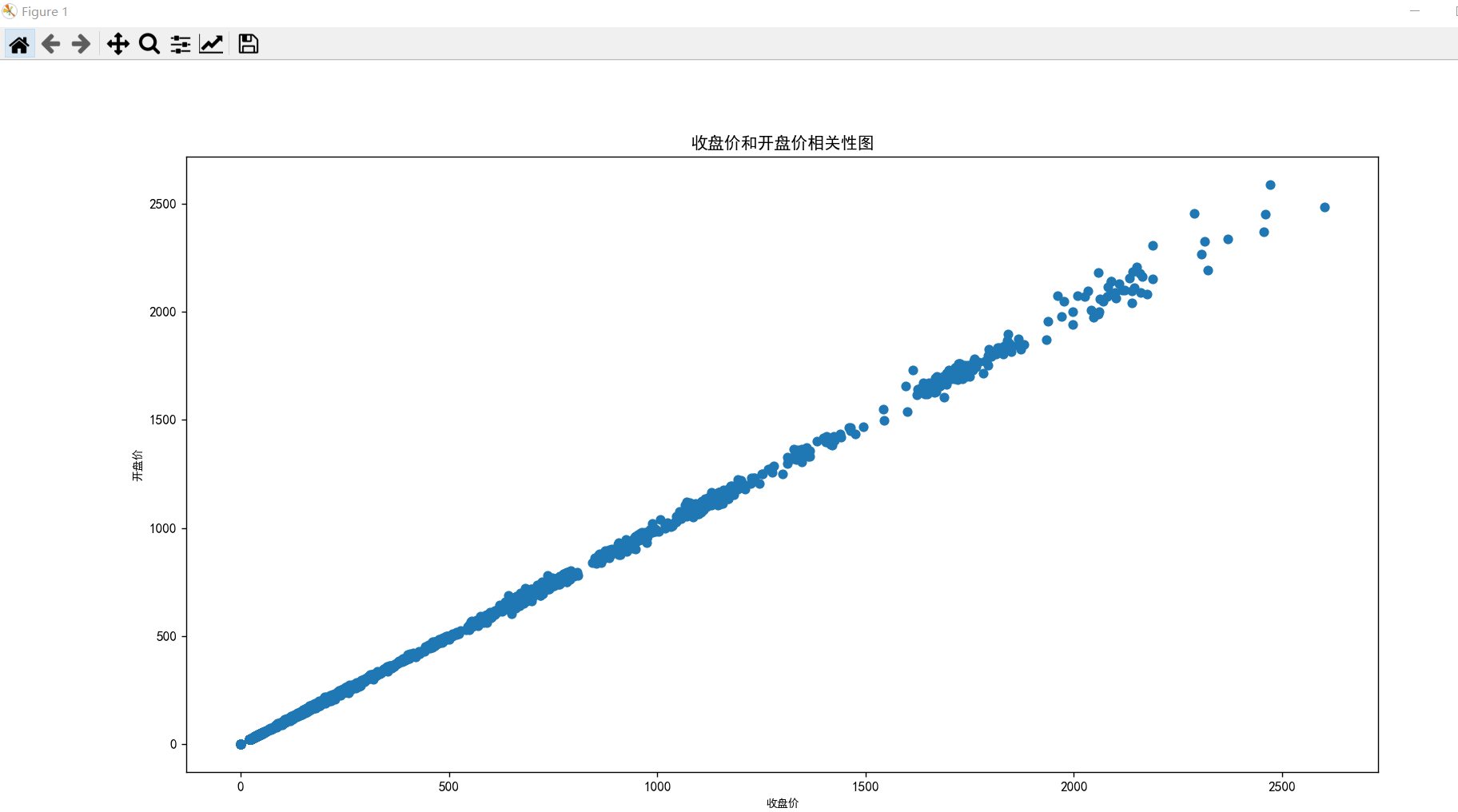

1-4-3 涨跌幅 换手率 

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("涨跌幅和换手率相关性图")
plt.xlabel('收盘价', fontsize=8)
plt.ylabel('换手率', fontsize=8)
plt.scatter(data["收盘价"].values, data["换手率"].values)
plt.show()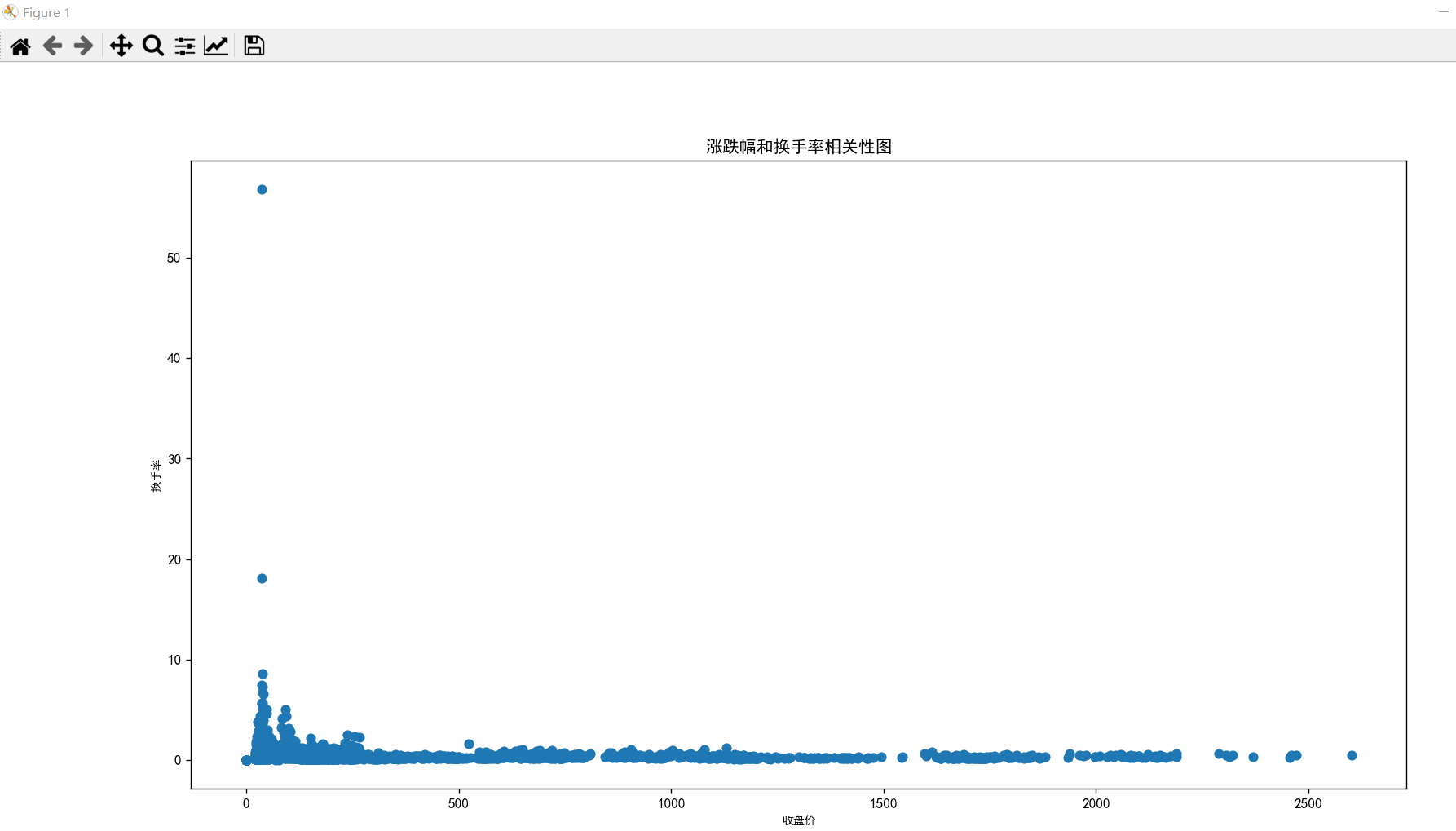

1-4-4 成交量 总市值

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("成交量和总市值相关性图")
plt.xlabel('成交量', fontsize=8)
plt.ylabel('总市值', fontsize=8)
plt.scatter(data["成交量"].values, data["总市值"].values)
plt.show()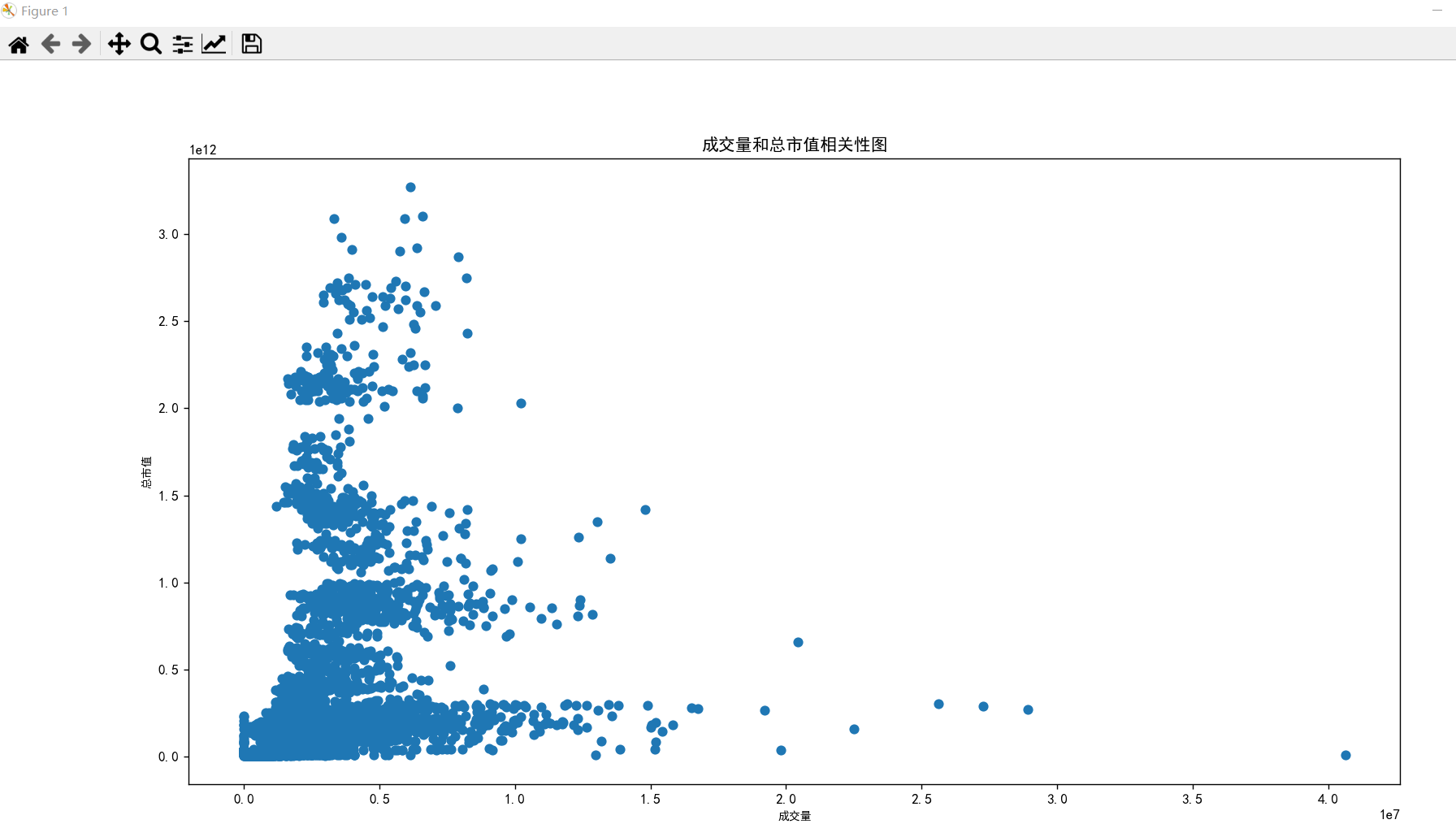

1-5 热力图数据分析 

# 热力图
ax = plt.subplots(figsize=(20, 16))
ax = sns.heatmap(data.corr(), vmax=.8, square=True, annot=True)
plt.show()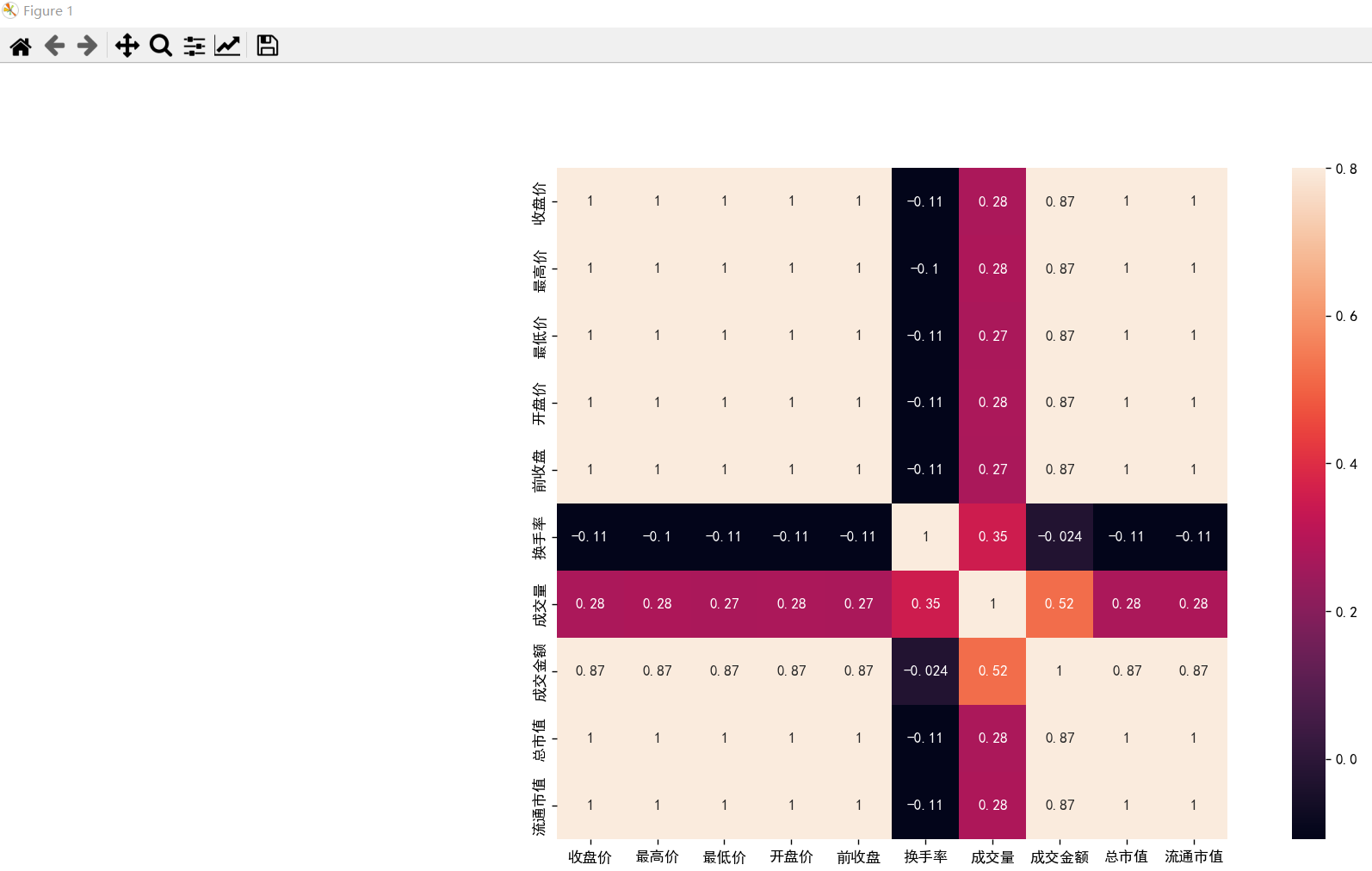

1-6 直方图数据分析 

1-6-1 成交量直方图

# 直方图
sz_close = data["成交量"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('成交量', fontsize=8)
plt.title("成交量直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()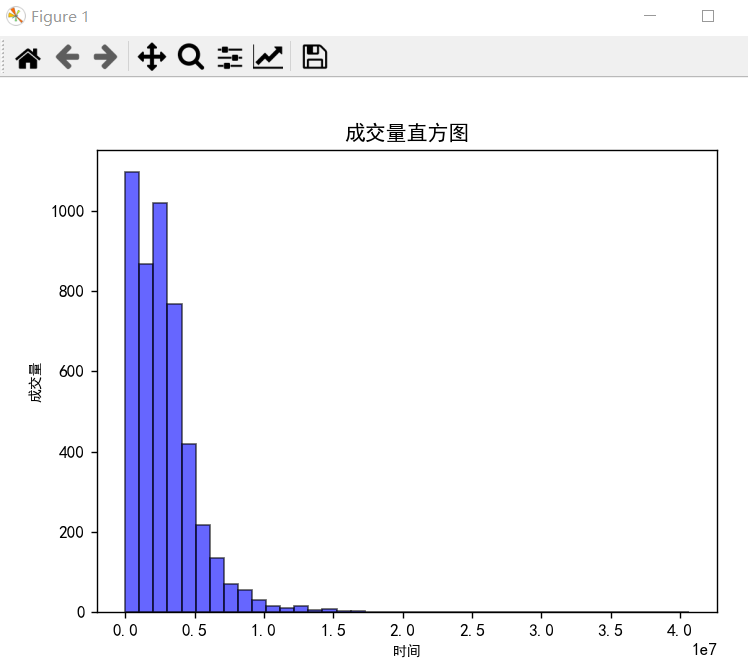

1-6-2 收盘价直方图

sz_close = data["收盘价"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('收盘价', fontsize=8)
plt.title("收盘价直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()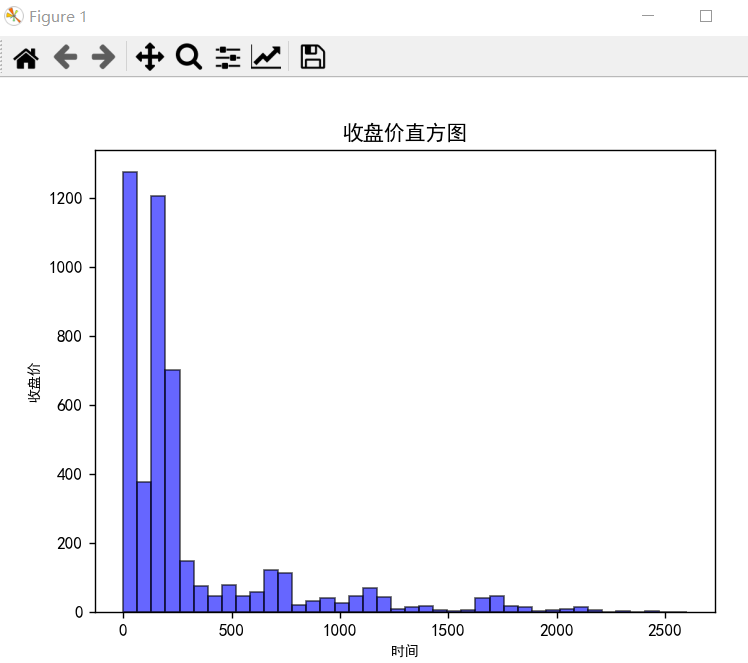

1-6-3 最高价直方图 

sz_close = data["最高价"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('最高价', fontsize=8)
plt.title("最高价直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()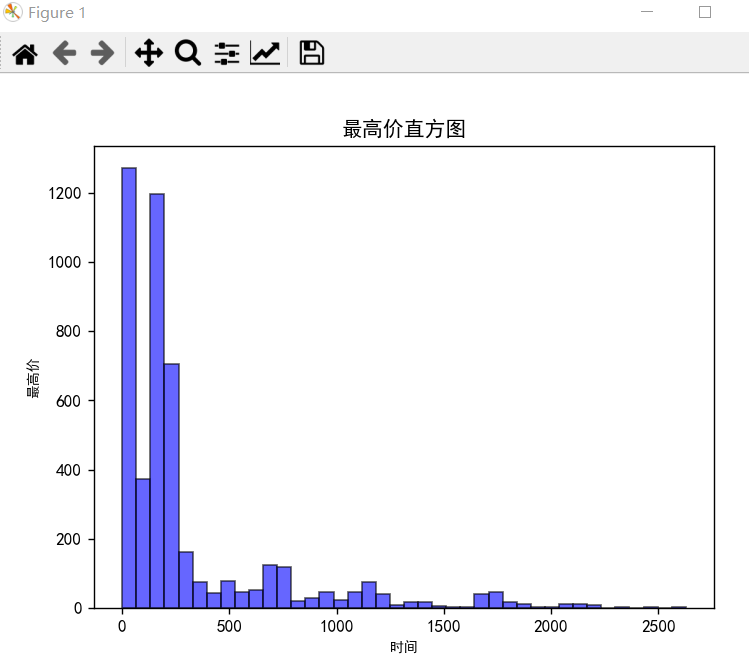

1-6-4 开盘价直方图

sz_close = data["开盘价"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('开盘价', fontsize=8)
plt.title("开盘价直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()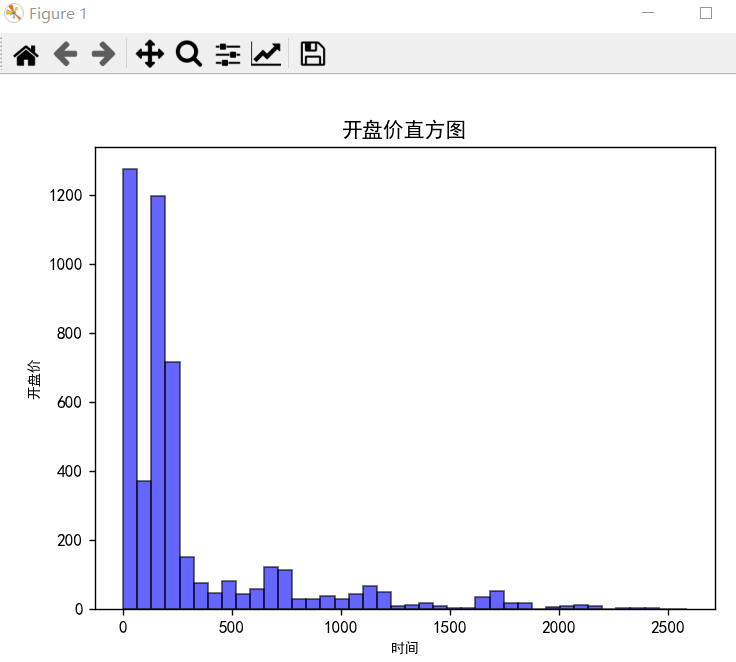

1-6-5 成交金额直方图

sz_close = data["成交金额"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('成交金额', fontsize=8)
plt.title("成交金额直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()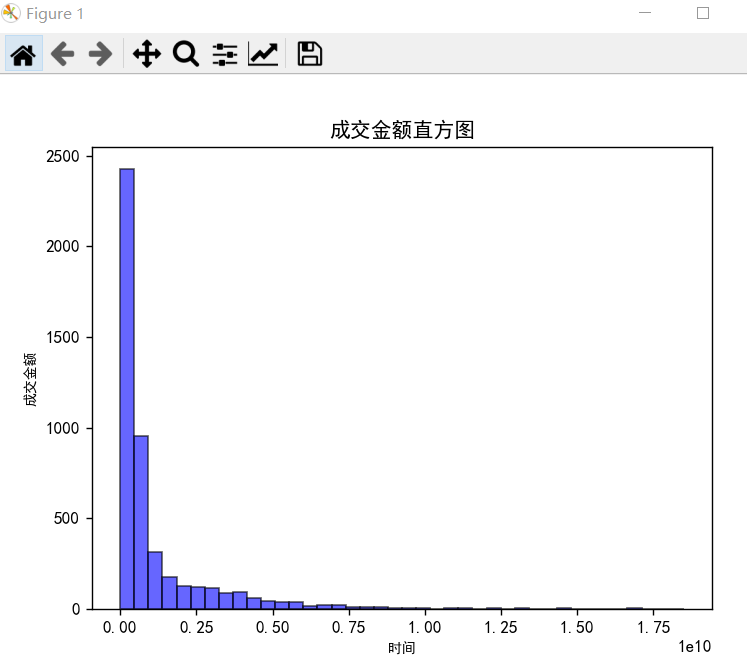

股票预测数据分析，完整源码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

data = pd.read_csv("stock.csv", encoding='gbk')
print(data.head())

# Index(['收盘价', '最高价', '最低价', '开盘价', '前收盘', '涨跌额', '涨跌幅', '换手率', '成交量', '成交金额','成交量', '流通市值'],
# 删除不需要的列
data.drop(['股票代码', '名称', '日期', ], axis=1, inplace=True)  # 删除操作  # '涨跌额','涨跌幅','成交金额','总市值','流通市值','成交量','换手率'
# 空值所在行删除
data = data.dropna(axis=0, how='any')
print(data.head())
print(data.columns)  # 打印表头

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("收盘价和前收盘相关性图")
plt.xlabel('收盘价', fontsize=8)
plt.ylabel('前收盘', fontsize=8)
plt.scatter(data["收盘价"].values, data["前收盘"].values)
plt.show()

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("收盘价和开盘价相关性图")
plt.xlabel('收盘价', fontsize=8)
plt.ylabel('开盘价', fontsize=8)
plt.scatter(data["收盘价"].values, data["开盘价"].values)
plt.show()

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("涨跌幅和换手率相关性图")
plt.xlabel('收盘价', fontsize=8)
plt.ylabel('换手率', fontsize=8)
plt.scatter(data["收盘价"].values, data["换手率"].values)
plt.show()

# 两类相关性分析
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16, 8))
plt.title("成交量和总市值相关性图")
plt.xlabel('成交量', fontsize=8)
plt.ylabel('总市值', fontsize=8)
plt.scatter(data["成交量"].values, data["总市值"].values)
plt.show()

# 热力图
ax = plt.subplots(figsize=(20, 16))
ax = sns.heatmap(data.corr(), vmax=.8, square=True, annot=True)
plt.show()

# 直方图
sz_close = data["成交量"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('成交量', fontsize=8)
plt.title("成交量直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()

sz_close = data["收盘价"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('收盘价', fontsize=8)
plt.title("收盘价直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()

plt.show()
sz_close = data["最高价"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('最高价', fontsize=8)
plt.title("最高价直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()

plt.show()
sz_close = data["开盘价"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('开盘价', fontsize=8)
plt.title("开盘价直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()

plt.show()
sz_close = data["成交金额"].values
x_close = [i for i in range(len(sz_close))]
plt.xlabel('时间', fontsize=8)
plt.ylabel('成交金额', fontsize=8)
plt.title("成交金额直方图")
plt.hist(sz_close, bins=40, facecolor="blue", edgecolor="black", alpha=0.6)
# 显示图标题
plt.show()

二：K线图数据分析

2-1 导入需要使用到的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import mpl_finance as mpf

from matplotlib.pylab import date2num
import datetime

2-2 读取表头数据

data = pd.read_csv("stock.csv", encoding='gbk')
data.drop(['股票代码', '名称'], axis=1, inplace=True)
# Index(['收盘价', '最高价', '最低价', '开盘价', '前收盘', '涨跌额', '涨跌幅', '换手率', '成交量', '成交金额','成交量', '流通市值'],
print(data.head())

          日期      收盘价      最高价  ...         成交金额           总市值          流通值
     0  2021/3/15  1975.45  2069.80  ...  12459955712  2.480000e+12  2.480000e+12
     1  2021/3/12  2026.00  2077.00  ...   8181594631  2.550000e+12  2.550000e+12
     2  2021/3/11  2048.00  2079.99  ...  11521736384  2.570000e+12  2.570000e+12
     3  2021/3/10  1970.01  1999.87  ...  10136910284  2.470000e+12  2.470000e+12
     4   2021/3/9  1936.99  2000.00  ...  16100769579  2.430000e+12  2.430000e+12

     [5 rows x 13 columns]

2-3 峰值数据分析

print(max(data["开盘价"].values), max(data["前收盘"].values), max(data["最高价"].values), max(data["最低价"].values))

2587.98 2601.0 2627.88 2485.0

2-4 数据转换为可读格式

# 将Tushare库中获取到的日期数据转换成candlestick_ochl()函数可读取的格式
def date_to_num(dates):
    num_time = []
    for date in dates:
        date_time = datetime.datetime.strptime(date, '%Y/%m/%d')
        num_date = date2num(date_time)
        num_time.append(num_date)
    return num_time

2-5 日期格式转换数字格式

# 将DataFrame转换为二维数组，并利用date_to_num()函数转换日期格式
df_arr = data.values  # 将DataFrame格式的数据转换为二维数组
# df_arr
df_arr[:, 0] = date_to_num(df_arr[:, 0])  # 将二维数组中的日期转换成数字格式
print(df_arr)

[[18701.0 1975.45 2069.8 ... 12459955712 2480000000000.0 2480000000000.0]
 [18698.0 2026.0 2077.0 ... 8181594631 2550000000000.0 2550000000000.0]
 [18697.0 2048.0 2079.99 ... 11521736384 2570000000000.0 2570000000000.0]
 ...
 [11563.0 36.38 37.0 ... 194689620 9095000000.0 2601170000.0]
 [11562.0 36.86 37.0 ... 463463143 9215000000.0 2635490000.0]
 [11561.0 35.55 37.78 ... 1410347179 8887500000.0 2541825000.0]]

2-6 绘制K线图

fig, ax = plt.subplots(figsize=(15, 6))
mpf.candlestick_ochl(ax, df_arr, width=0.6, colorup='r', colordown='g', alpha=1.0)
plt.grid()  # 显示网格
ax.xaxis_date()  # 设置x轴的刻度格式为常规日期格式
plt.show()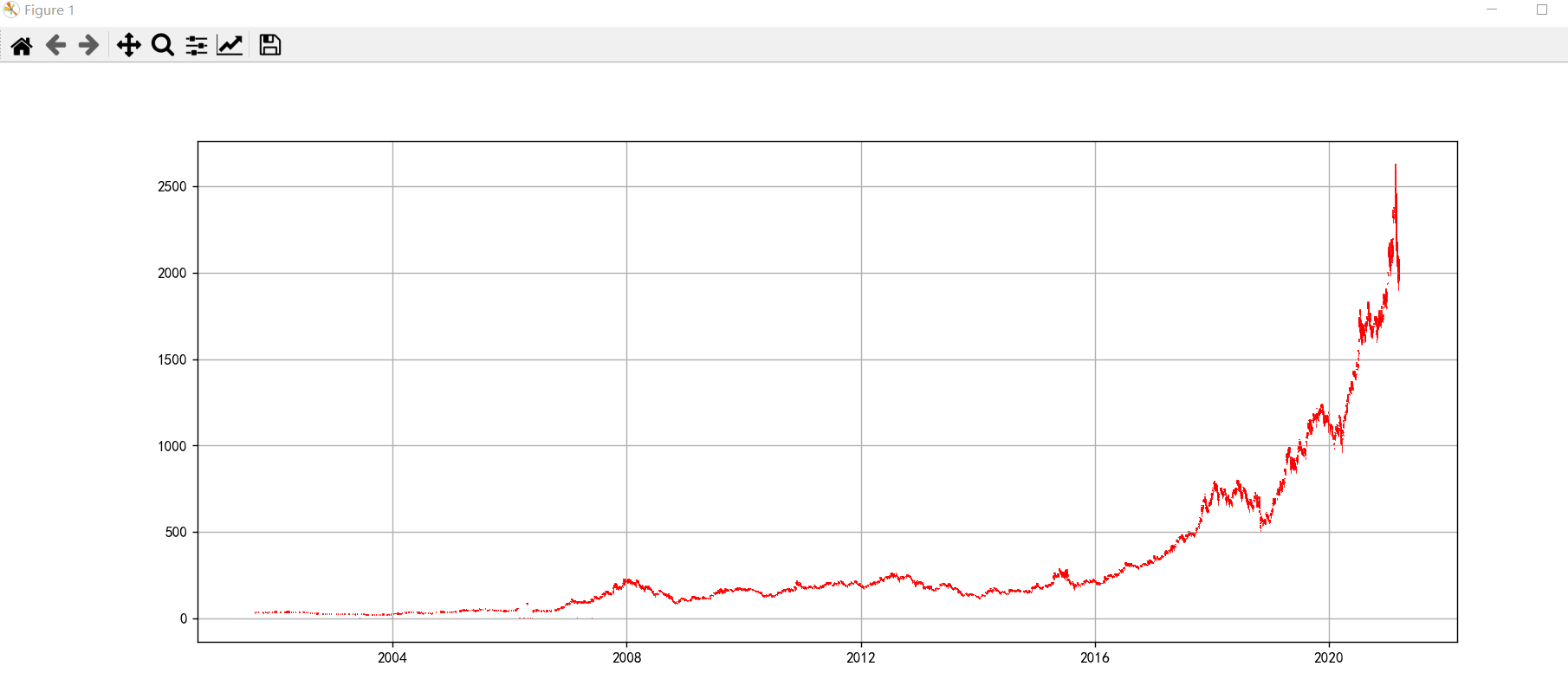

K线图数据分析，完整源码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import mpl_finance as mpf

data = pd.read_csv("stock.csv", encoding='gbk')
data.drop(['股票代码', '名称'], axis=1, inplace=True)
# Index(['收盘价', '最高价', '最低价', '开盘价', '前收盘', '涨跌额', '涨跌幅', '换手率', '成交量', '成交金额','成交量', '流通市值'],
# print(data.head())
# print(max(data["开盘价"].values), max(data["前收盘"].values), max(data["最高价"].values), max(data["最低价"].values))

# 导入调整日期格式涉及的两个库
from matplotlib.pylab import date2num
import datetime


# 将Tushare库中获取到的日期数据转换成candlestick_ochl()函数可读取的格式
def date_to_num(dates):
    num_time = []
    for date in dates:
        date_time = datetime.datetime.strptime(date, '%Y/%m/%d')
        num_date = date2num(date_time)
        num_time.append(num_date)
    return num_time


# 将DataFrame转换为二维数组，并利用date_to_num()函数转换日期格式
df_arr = data.values  # 将DataFrame格式的数据转换为二维数组
# df_arr
df_arr[:, 0] = date_to_num(df_arr[:, 0])  # 将二维数组中的日期转换成数字格式
print(df_arr)
fig, ax = plt.subplots(figsize=(15, 6))
mpf.candlestick_ochl(ax, df_arr, width=0.6, colorup='r', colordown='g', alpha=1.0)
plt.grid()  # 显示网格
ax.xaxis_date()  # 设置x轴的刻度格式为常规日期格式
plt.show()