👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
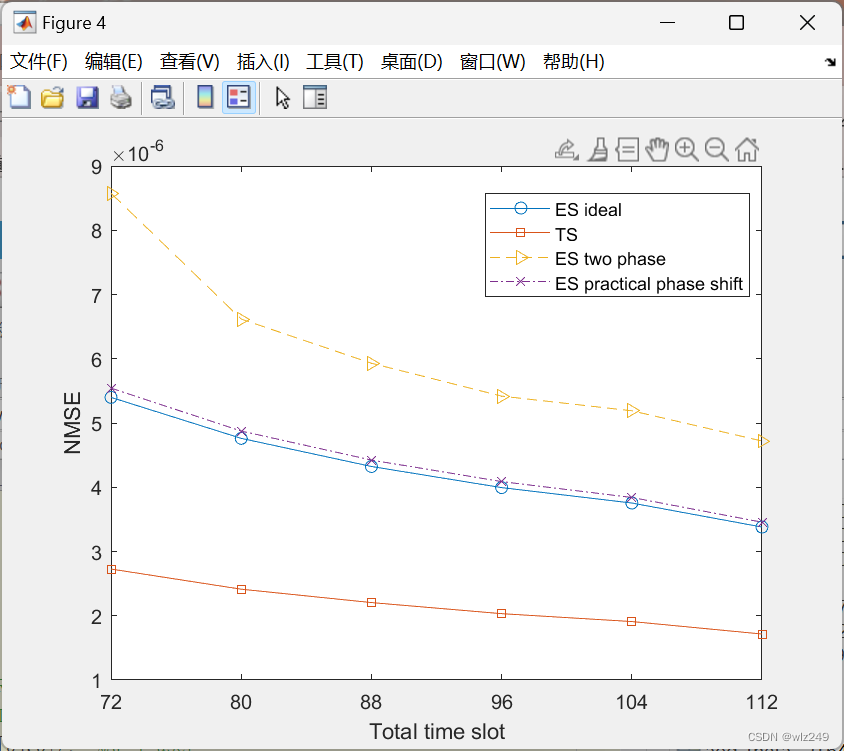
📚2 运行结果
🌈3 Matlab代码实现
🎉4 参考文献
💥1 概述
基于离散傅里叶变换的系统,如正交频分复用(OFDM)和单载波频分多址(SC-FDMA),特别容易发生带外漏电。尽管已经提出了许多技术来抑制基于DFT的系统中的旁瓣,但计算复杂性和带外功率泄漏之间的令人满意的平衡仍然难以实现。 正交预编码是一种很有前途的线性技术,其中具有正交列的预编码矩阵的零空间旨在抑制旁瓣。特别是,Xu 和 Chen [1]、van de Beek [2] 和 Ma 等人 [3] 提出了产生出色带外抑制的正交预编码器。然而,它们的算术复杂性高---有源子载波数量的二次---这限制了它们的应用。 在本文中发现,如果使用块反射器而不是非结构化的酉变换来执行预编码,则算术复杂度可以变为线性而不是二次。实现的误码率无需支付任何惩罚。通过数值模拟表明,OFDM在峰均功率比方面的损失也非常小。
📚2 运行结果
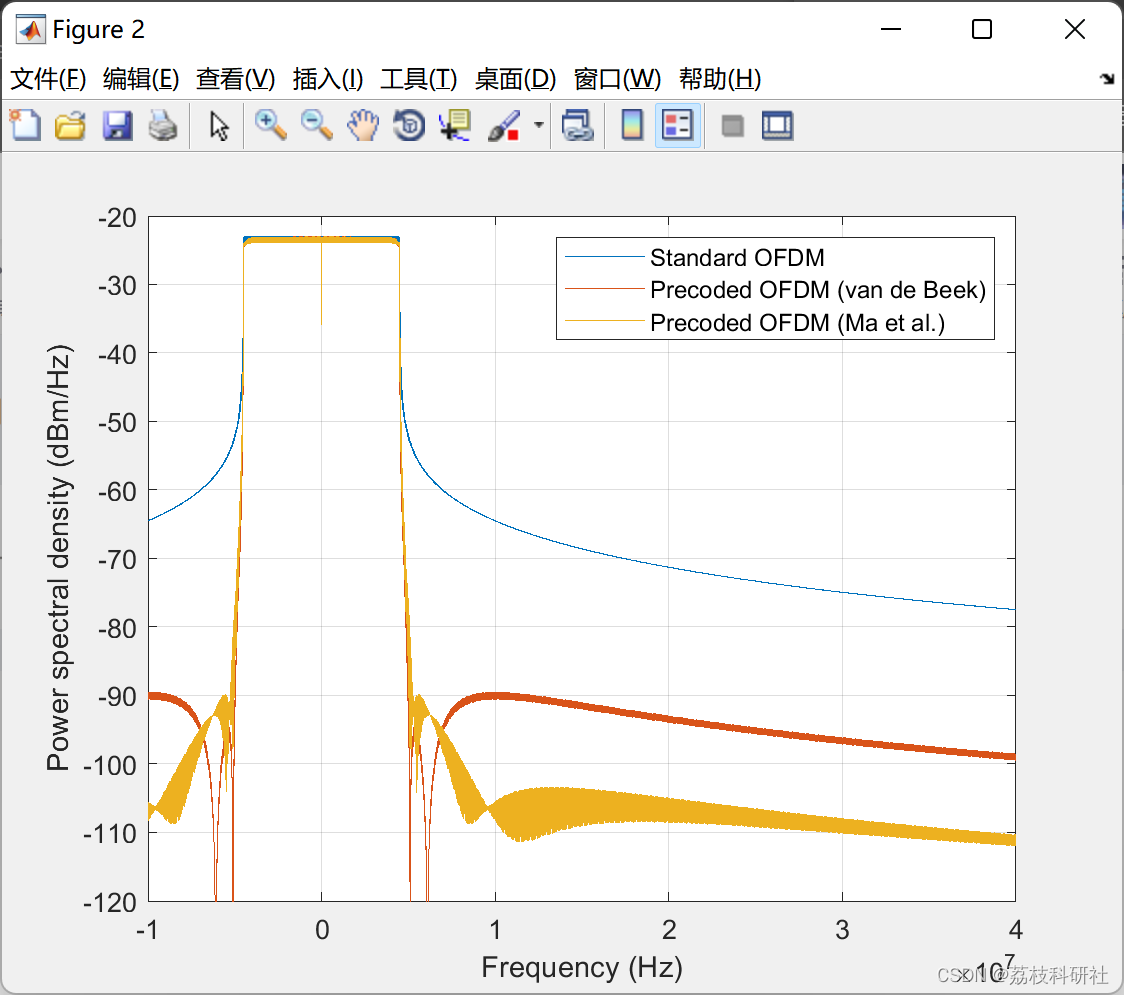
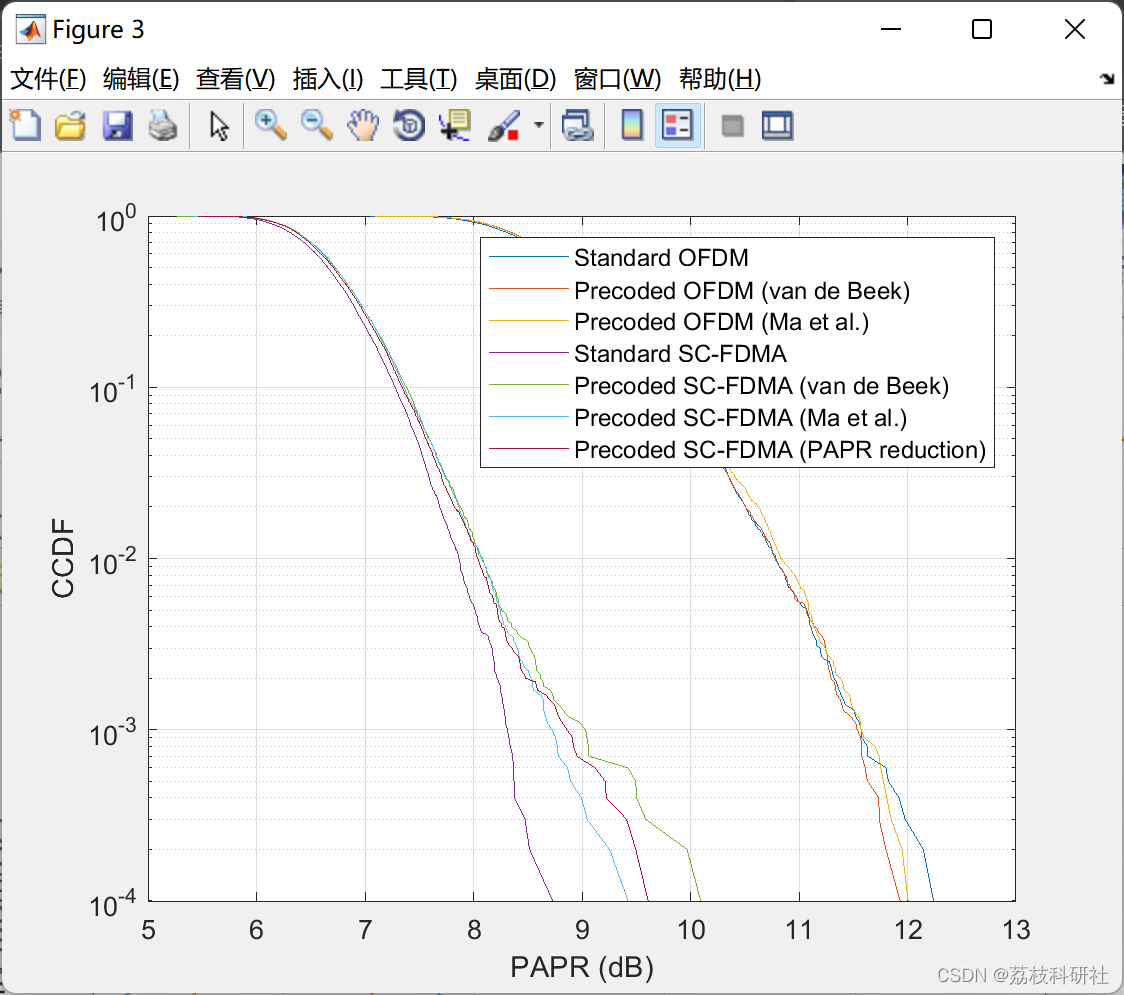
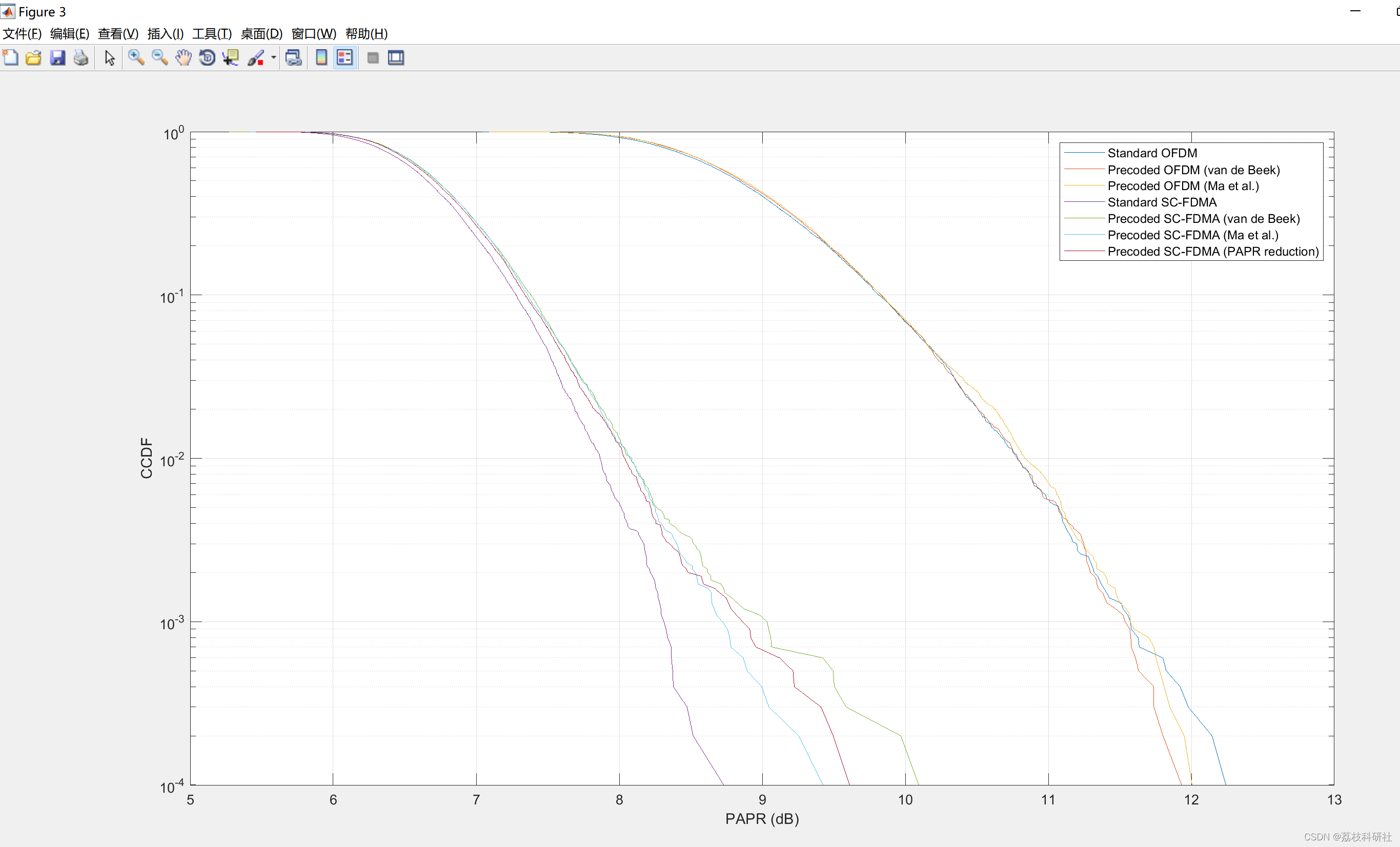
部分代码:
figure(2);
PtotdBm = 46; % Total downlink power in dBm
Ptot = 1e-3 * 10^(PtotdBm/10); % same in W
S = [-300:-297, 297:300, -296:-1, 1:296]; % set of active sub-carriers (permuted!)
Psub = Ptot / length(S); % power per subcarrier (W)
Ts = 1e-3/15; % data length (in seconds)
Tg = 9*Ts/128; % cyclic prefix length (s)
T = Ts + Tg;
f = -10e6:0.005e6:40e6; % array of sample frequencies for plotting
kfTs = S' * ones(size(f)) - ones(size(S))' * f * Ts; % k - f Ts
a = sqrt(Psub) * T * exp(j*pi*(1-Tg/Ts)*kfTs) .* sinc((1+Tg/Ts)*kfTs);
% (11) but not forgetting the scaling factors
plot(f, 10*log10(sum(abs(a).^2)/(1e-3*T)), 'DisplayName', 'Standard OFDM');
grid on;
hold on;
M = [-6101, -6099, -5101, -5099, 5099, 5101, 6099, 6101] * 1e3; % nulling frequencies
R = length(M);
kMTs = S' * ones(size(M)) - ones(size(S))' * M * Ts; % k - M Ts
A2 = exp(j*pi*(1-Tg/Ts)*kMTs)' .* sinc((1+Tg/Ts)*kMTs)'; % (15)
% [~, ~, V] = svd(A2); % (7)
Gvdb = blockreflector2(A2');
V = eye(length(S)) - Gvdb*Gvdb';
Go = V(:, (R+1):length(S)); % (8)
plot(f, 10*log10(sum(abs(Go'*a).^2)/(1e-3*T)), ...
'DisplayName', 'Precoded OFDM (van de Beek)');
% Skipping N-continuous OFDM that was originally a part of Fig. 3(a)...
% Now add the comparison with Ma et al. technique
phi = [-40e6:0.2e6:-5e6, 5e6:0.2e6:40e6]; % spectral leakage frequencies
kpTs = S' * ones(size(phi)) - ones(size(S))' * phi * Ts; % k - phi Ts
C = exp(j*pi*(1-Tg/Ts)*kpTs)' .* sinc((1+Tg/Ts)*kpTs)';
[~, ~, Vma] = svd(C);
Gma = blockreflector2(Vma(:, 1:R));
V = eye(length(S)) - Gma*Gma';
Popt = V(:, (R+1):length(S));
plot(f, 10*log10(sum(abs(Popt'*a).^2)/(1e-3*T)), ...
'DisplayName', 'Precoded OFDM (Ma et al.)');
hold off;
ylim([-120, -20]);
xlabel('Frequency (Hz)');
ylabel('Power spectral density (dBm/Hz)');
legend(gca, 'show');
% added for Code Ocean output
% save the resulting plot to an HTML file using Plotly.js
% fig2plotly(gcf, 'offline', true, 'filename', 'figure1');
% finally, save the resulting plot to a PNG file (note the output directory)
saveas(gcf, 'figure1.fig');
% Figure 3. Now move on to PAPR calculations.
figure(3);
ie = 4; % use ie = 7 to get the same quality of results as in the paper
numiter = 10^ie; % number of Monte Carlo iterations for PAPR calculations
subsamp = unique(round(numiter+1-10.^(ie:-0.01:0))); % for subsampling
numsub = 2048; % number of subcarriers available
prefix = numsub * Tg / Ts; % number of samples in the cyclic prefix
X = zeros(1, numsub);
papr = zeros(1, numiter);
% Standard OFDM with QPSK
l=8; % oversampling factor for PSD estimation (min value = 2)
Y1 = zeros(1, l*numsub);
Y2 = zeros(1, l*numsub);
Y3 = zeros(1, l*numsub);
Y5 = zeros(1, l*numsub);
Y6 = zeros(1, l*numsub);
Y7 = zeros(1, l*numsub);
timing = zeros(1, 7);
tic;
for i=1:numiter
d = sqrt(Psub/2) * (2*randi(2, size(S)) + 2*j*randi(2, size(S)) - 3 - 3*j); % QPSK data vector
X(S+numsub/2) = d;
x = numsub*ifft(ifftshift(X));
% Y = [zeros(1, (l/2-1)*numsub/2), X, zeros(1, (l/2-1)*numsub/2)];
% y = l*numsub*ifft(ifftshift(Y))/2;
% y1 = [y((l*(numsub-prefix)/2+1):l*numsub/2), y, zeros(1, l*(numsub-prefix)/2)];
% Y1 = Y1 + 4*Ts^2*abs(fft(y1)/(l*numsub)).^2/(Ts+Tg);
papr(i) = numsub * max(abs(x).^2) / norm(x)^2;
end;
timing(1) = toc;
Y1 = Y1 / numiter;
papr = sort(papr);
semilogy(10*log10(papr), 1-(1:numiter)/numiter);
papr1 = papr(subsamp);
grid on;
hold on;
🌈3 Matlab代码实现
🎉4 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Clarkson, I. Vaughan L.. "Orthogonal precoding for sidelobe suppression in DFT-based systems using block reflectors." 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (2017)