命题逻辑

等值演算公式的使用【重点】

$((P\to Q)\wedge (Q\to R))\to (P\to R)$
$\iff \neg ((\neg P\vee Q)\wedge (\neg Q\vee R))\vee (\neg P\vee R)$
$\iff \neg (\neg P\vee Q)\vee \neg (\neg Q\vee R)\vee \neg P\vee R$
$\iff (P\wedge \neg Q)\vee (Q\wedge \neg R)\vee \neg P\vee R$
$\iff ((P\wedge \neg Q)\vee \neg P)\vee ((Q\wedge \neg R)\vee R)$
$\iff ((P\vee \neg P)\wedge (\neg Q\vee \neg P))\vee ((Q\vee R)\wedge (\neg R\vee R))$
$\iff (1\wedge (\neg Q\vee \neg P))\vee ((Q\wedge R)\wedge 1)$
$\iff (\neg Q\vee \neg P)\vee (Q\vee R)$
$\iff (\neg Q\vee Q)\vee \neg P\vee R$
$\iff 1\vee \neg P\vee R$
$\iff 1$
$\therefore 此公式为重言式$

• 解题思路：

  • 先消掉$\to \iff$
  • 括号$()$前面的$\neg$，用德摩根律
  • 多层结构变单层，能化简到化简，能消掉的消掉（同一律，零律，矛盾律，排中律，双重否定律，吸收律，密等律）
  • 使用交换律，结合律，把相同的变元或子公式放到一起来化简单
  • 注意吸收律有时很有用$P\wedge (((R\vee Q)\wedge \neg Q)\vee P)\iff P$
  • 证明2个公式等价时一般从复杂公式向简单公式方向变换，但如果2个公式的复杂程度差不多，则都可以尝试变换，更容易找到思路。

• 等值演算也是考试德重要内容，作者就不在这里过多举例了。都是固定的套路

• 编辑公式太耗时了，希望大家把平时的课后题和例题好好看看、做做。

析取范式和合取范式【重点】

• 文字:命题变项及其否定的总称，例如：p, ¬p
• 简单析取式:有限个文字构成的析取式，如 p, ¬q, p∨¬q, p∨q∨r, …
• 简单合取式:有限个文字构成的合取式，如 p, ¬q, p∧¬q, p∧q∧r
• 析取范式:由有限个简单合取式组成的析取式A1∨A2∨…∨Ar, 其中A1,A2,…,Ar是简单合取式。例如: (p∧¬q)∨(p∧q∧r)
• 合取范式:由有限个简单析取式组成的合取式A1∧A2∧…∧Ar , 其中A1,A2,…,Ar是简单析取式。例如: (p∨¬q)∧(p∨q∨r)
• 范式:析取范式与合取范式的统称

范式存在定义【了解】

• 定理任何命题公式都存在着与之等值的析取范式与合取范式

求公式A的范式的步骤：【重点】

1. 消去A中的→, ↔（若存在）
2. 否定联结词¬的内移或消去
3. 使用分配律
   • ∧对∨分配（析取范式）
   • ∨对∧分配（合取范式）

• 公式的范式存在，但不惟一

极大项和极小项【重点】

• 定义
  • 在含有n个命题变项的简单合取式(简单析取式)中，若每个命题变项均以文字的形式在其中出现且仅出现一=次，而且第i（1≤i≤n）个文字出现在左起第i位上，称这样的简单合取式（简单析取式）为极小项（极大项）。
  • n个命题变项产生2n个极小项和2n个极大项
  • 用$m_i$表示第i个极小项，其中$i$是该极小项成真赋值的十进制表示. 用$M_i$表示第$i$个极大项，其中$i$是该极大项成假赋值的十进制表示, $m_i(M_i)$称为极小项(极大项)的名称。
  • $m_i$与$M_i$的关系: $\neg m_i\iff M_i,\neg M_i\iff m_i$
    
    
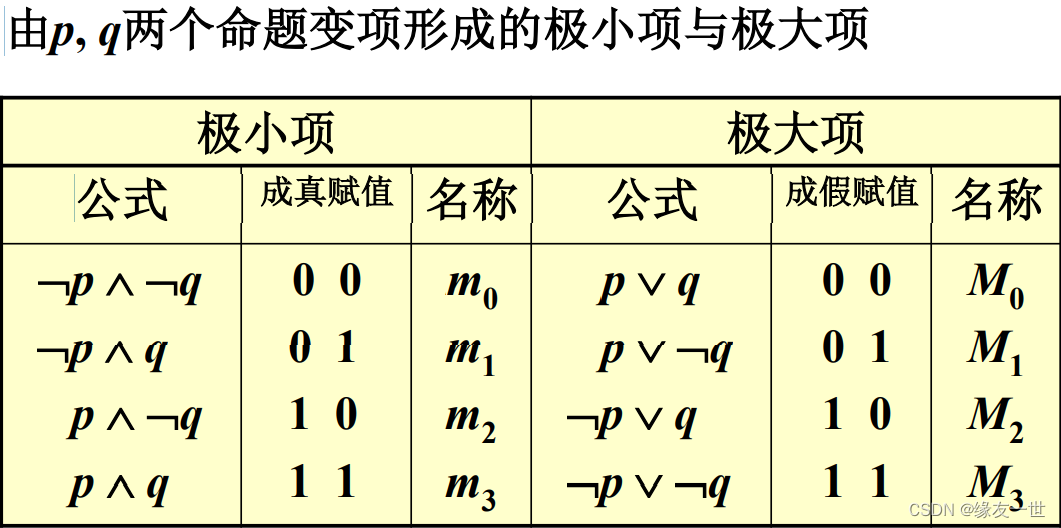
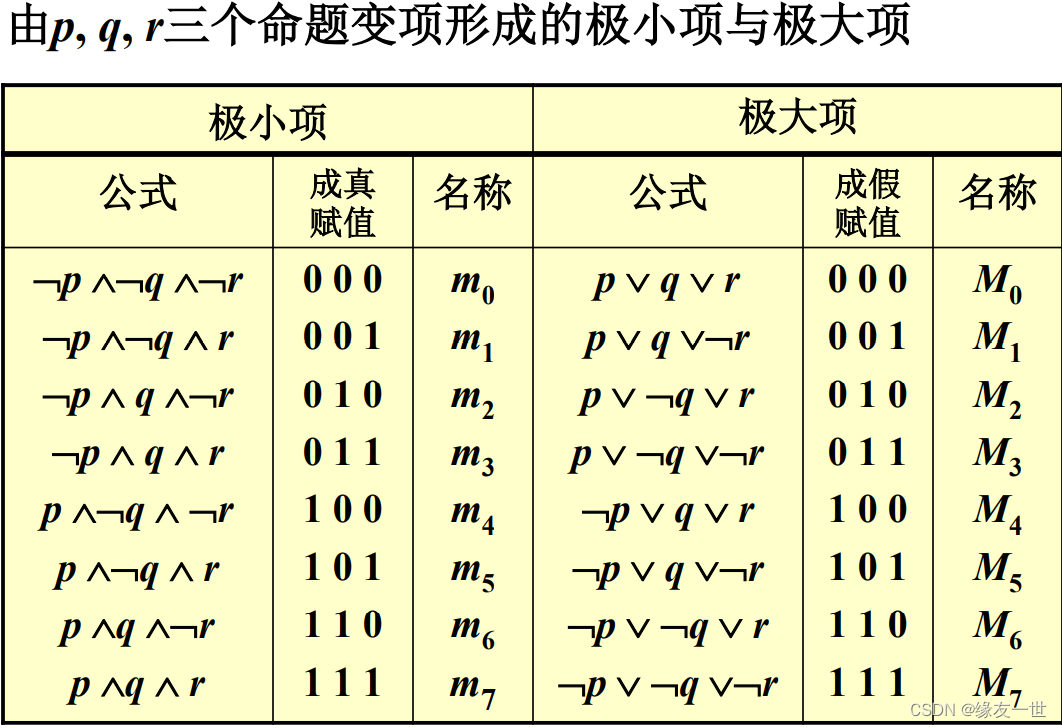
• 极大项和极小项的性质
  • 任意两个不同极小项的合取必为假；$m_i\wedge m_j=F,i\ne j$任意两个不同极大项的析取必为真；$M_i\vee M_j=T,i\ne j$
  • 极大项的否定是极小项；极小项的否定是极大项；
  • 所有极小项的析取为永真公式；所有极大项的合取是永假公式

主合取范式和主析取范式【重点】

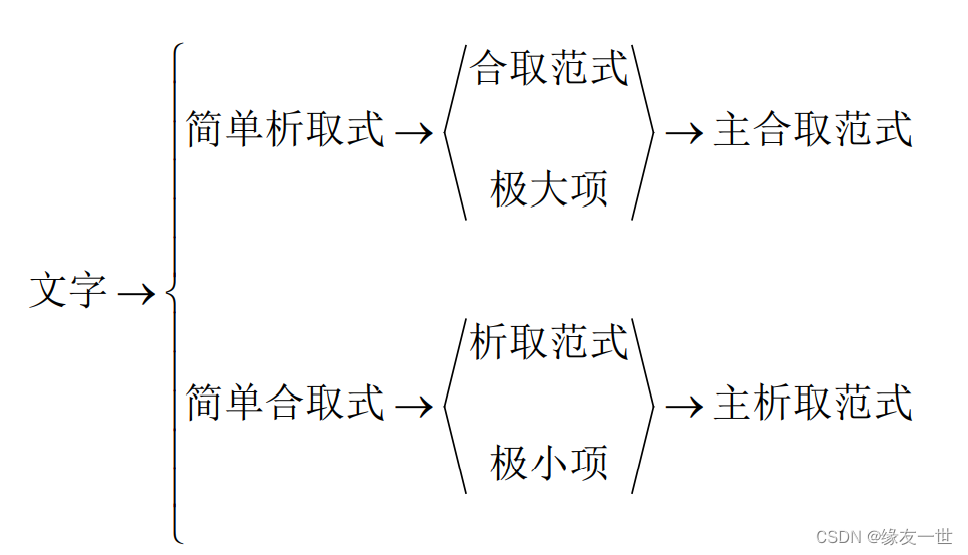
• 主析取范式=极小项(或小项,m,简单合取式)的析取A的主析取范式: 与A等值的主析取范式
• 主合取范式=极大项(或大项,M,简单析取式)的合取A的主合取范式: 与A等值的主合取范式
• m的下标确定：每个变元有$\neg$为0，没有为1
• M的下标确定：每个变元有$\neg$为1，没有为0
  
  

等式演算求主析取范式【重点】

真值表求主析取范式【了解】

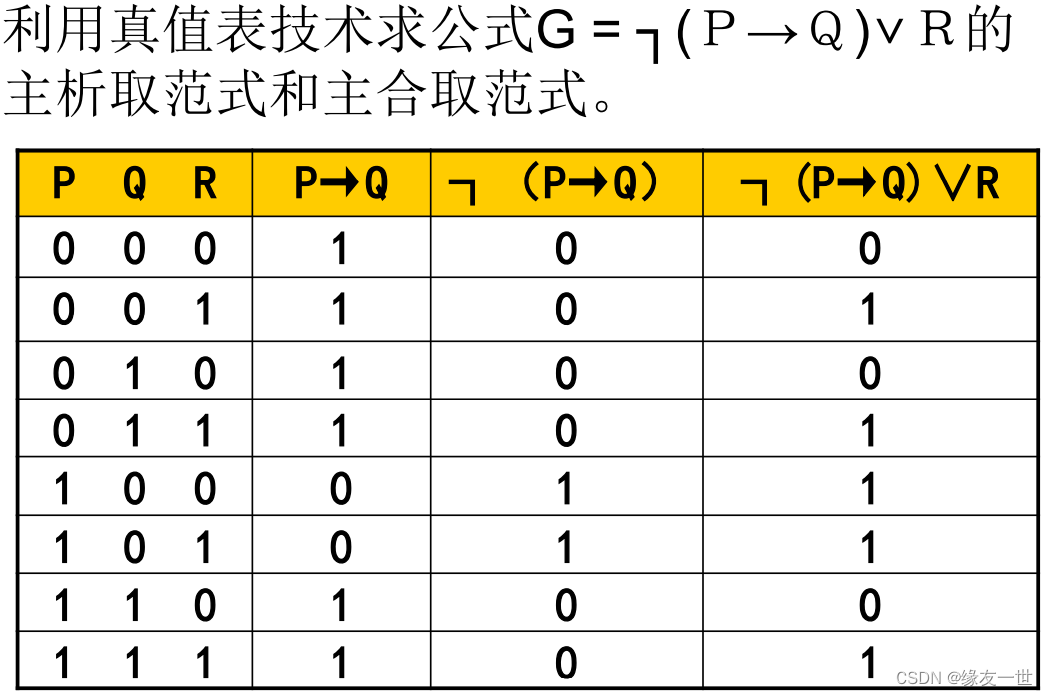
主范式的应用【重点】

1. 求公式的成真赋值和成假赋值

   • 在主析取范式的结果中，全部都是成真赋值；在主合取范式的结果中，全部都是成假赋值
   • 例如 $(p\to \neg q)\to r\iff m_1\vee m_3\vee m_5\vee m_6\vee m_7$
     • 其成真赋值为001, 011, 101, 110, 111，
     • 其余的赋值 000, 010, 100为成假赋值

2. 判断公式的类型

   • 设A含n个命题变项，则A为重言式⇔A的主析取范式含$2^n$个极小项⇔A的主合取范式为1.
   • A为矛盾式⇔ A的主析取范式为0⇔ A的主合取范式含$2^n$个极大项
   • A为非重言式的可满足式
     ⇔A的主析取范式中至少含一个且不含全部极小项
     ⇔A的主合取范式中至少含一个且不含全部极大

3. 判断两个公式是否等值
   

推理部分【了解】

• 推理有效，指的是它的结论是它前提的合乎逻辑的结果
• 如果它的前提都为真，那么所得的结论也必然为真，而并不是要求前提或结论一定为真或为假，如果推理是有效的话，那么不可能它的前提都为真时，而它的结论为假

推理的基本概念和推理形式【了解】

• 设G,H是公式，对任意解释I，如果I满足G，那么I满足H，则称H是G的逻辑结果(或称G蕴涵H),记为G⇒Ｈ，此时称G为前提，H为结论

判定定理【了解】

• 定理一：设G,H是公式，H是G的逻辑结果当且仅当G→Ｈ为永真公式。
• 定理二：公式H是前提集合$Г=G_1,G_2,\dots ,G_n$的逻辑结果当且仅当$G_1\wedge G_2\wedge \dots \wedge G_n\to Ｈ$为永真公式。

推理的形式结构

• 前提：$A_1,A_2,\dots ,A_k$
• 结论： B
• 若推理正确，则记作：$A_1\wedge A_2\wedge \dots \wedge A_k\Rightarrow B$

判断推理是否正确的方法

• 解题步骤：
  1. 将命题符号化
  2. 写出前提、结论或推理的形式结构
  3. 判断或证明推理结果是否正确,也就是判断一个蕴含式是否是重言.

真值表法

• 证明$(p\to q)\wedge p\Rightarrow q$
  • 列出$(p\to q)\wedge p\to q$真值表为

p q	$(p\to q)\wedge p\to q$
0 0	1
0 1	1
1 0	1
1 1	1

$\therefore$公式为重言式，即有$(p\to q)\wedge p\Rightarrow q$

等值演算的方法

• 推理正确 = 公式${\mathbf{A}}_1\wedge {\mathbf{A}}_2\wedge {\mathbf{A}}_3\wedge \cdots \wedge {\mathbf{A}}_{\mathbf{n}}\to \mathbf{B}$为重言式
• 判断推理是否正确
  • 若今天是1号，则明天是5号. 今天是1号. 所以明天是5号
  • p：今天是1号，q：明天是5号
  • 推理的形式结构为: $(p\to q)\wedge p\to q$
  • $(p\to q)\wedge p\to q$
    $\iff \neg ((\neg p\vee q)\wedge p)\vee q$
    $\iff \neg p\vee \neg q\vee q\iff 1$
    得证推理正确

主析取范式法

• 若今天是1号，则明天是2号. 明天是2号. 所以今天是1号
  • p：今天是1号，q：明天是2号
  • 推理的形式结构为: (p→q)∧q→p
  • $(p\to q)\wedge q\to p$
    $\iff (\neg p\vee q)\wedge q\to p$
    $\iff \neg ((\neg p\vee q)\wedge q)\vee p$
    $\iff \neg q\vee p$
    $\iff (\neg p\wedge \neg q)\vee (p\wedge \neg q)\vee (p\wedge \neg q)\vee (p\wedge q)$
    $\iff m_0\vee m_2\vee m_3$
  • 结果不含$m_1$, 故01是成假赋值，所以推理不正确.

直接证明法【重点】

• P：证明过程中引入前提时标记

• T：证明过程中推出新的结论时标记

• 要保证每个前提都是真是真的

• 前提：$p\vee q,p\to \neg r,s\to t,\neg s\to r,\neg t$

• 结论：$q$
  1️⃣$\neg t$-----------P
  2️⃣$s\to t$------P
  3️⃣$\neg s$-----------T1️⃣2️⃣
  4️⃣$\neg s\to r$—p
  5️⃣$r$-------------T3️⃣4️⃣
  6️⃣$p\to \neg r$----P
  7️⃣$\neg p$-----------T5️⃣5️⃣
  8️⃣$p\vee q$--------P
  9️⃣$q$--------------T7️⃣8️⃣

推理定律——重言蕴涵式

公式形式	公式名称
$A\Rightarrow (A\vee B)$	附加律
$(A\wedge B)\Rightarrow A$	化简律
$(A\to B)\wedge A\Rightarrow B$	假言推理
$(A\to B)\wedge \neg B\Rightarrow \neg A$	拒取式
$(A\vee B)\wedge \neg B\Rightarrow A$	析取三段论
$(A\to B)\wedge (B\to C)\Rightarrow (A\to C)$	假言三段论
$(A\leftrightarrow B)\wedge (B\leftrightarrow C)\Rightarrow (A\leftrightarrow C)$	等价三段论
$(A\to B)\wedge (C\to D)\wedge (A\vee C)\Rightarrow (B\vee D)$	构造性二难
$(A\to B)\wedge (\neg A\to B)\Rightarrow B$	构造性二难（特殊形式）
$(A\to B)\wedge (C\to D)\wedge (\neg B\vee \neg D)\Rightarrow (\neg A\vee \neg C)$	破坏性二难

构造证明法【重点，实在记不住就用直接证明法】

• 利用推理定义，进行证明