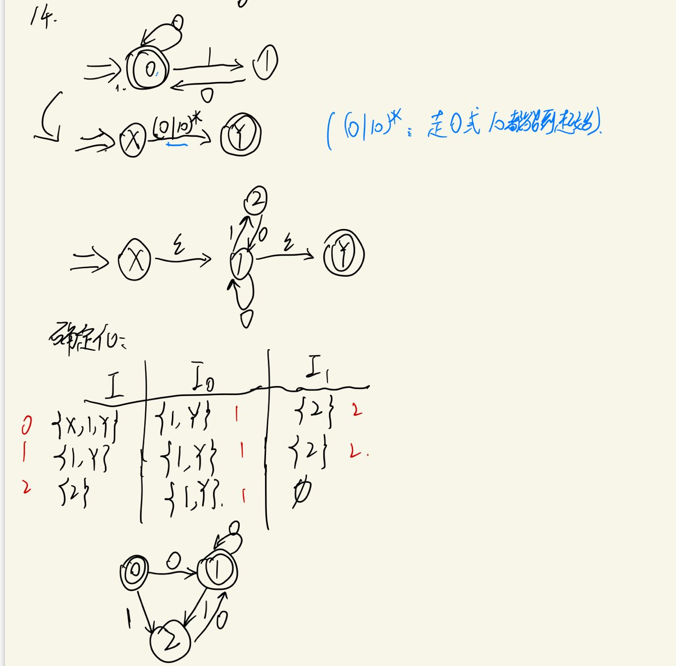一、DFA和NFA的区别

NFA：非确定有限自动机
DFA：确定有限自动机
NFA在同一状态，可以有多条出边，DFA在同一状态，只能有一条出边；
NFA的初态可以具有多个，DFA的初态是唯一的；

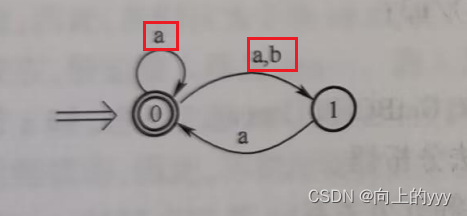
比如这个图就是NFA，因为0可以通过输入一个字符a到达本身，还可以通过a到达1，这就是在同一状态，有多条出边；

二、构造DFA

下图有三条重要的转换规则，在通过正规式构造NFA图时用到的；

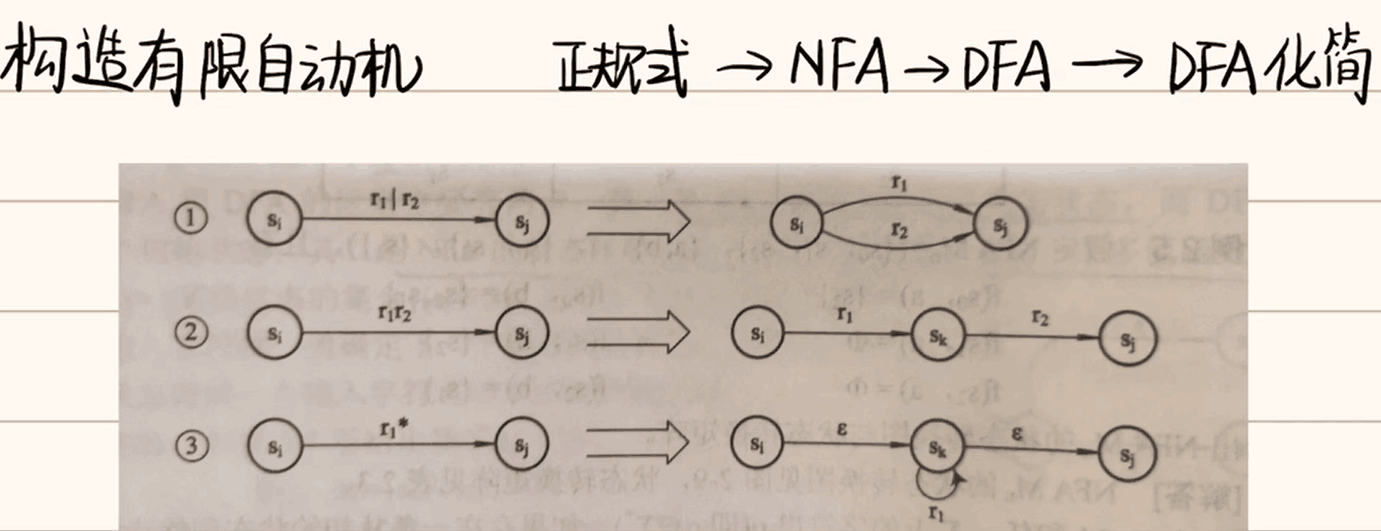
1. 通过正规式构造DFA（核心）

例题

这个题就是给你正规式，让你构造DFA，通过第一个正规式进行示例：

（1）把正规式转换为NFA

使用上面的三个规则，可以将正规式最终转化为一个NFA图

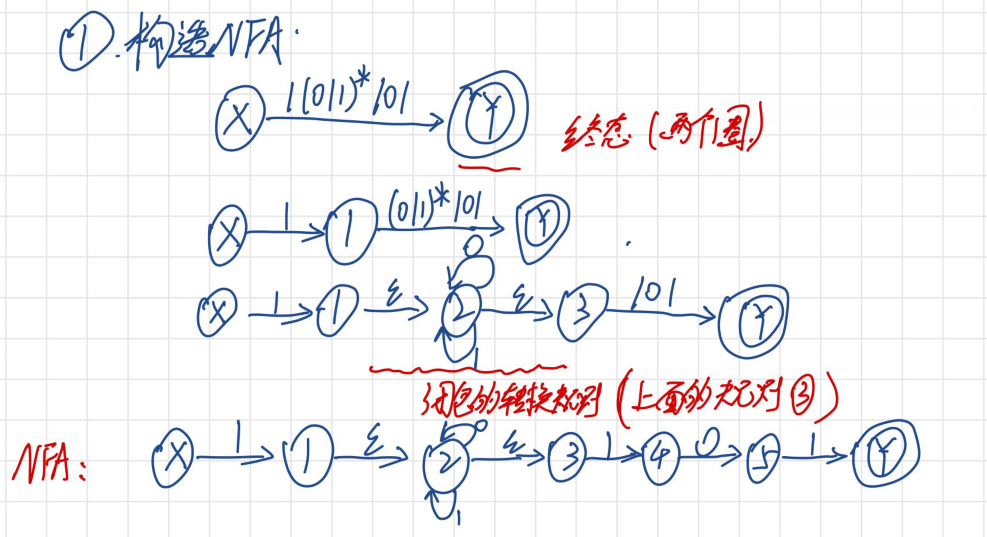
（2）把NFA通过子集构造法转换为DFA（确定化）

①先根据NFA图，画出状态转换矩阵如下：

②可以对矩阵进行编号，然后用其编号，画DFA的状态转换图：

③根据上面已经编过号的图，画出DFA的状态转换图，集合含终态的元素，注意要画两个圈圈；

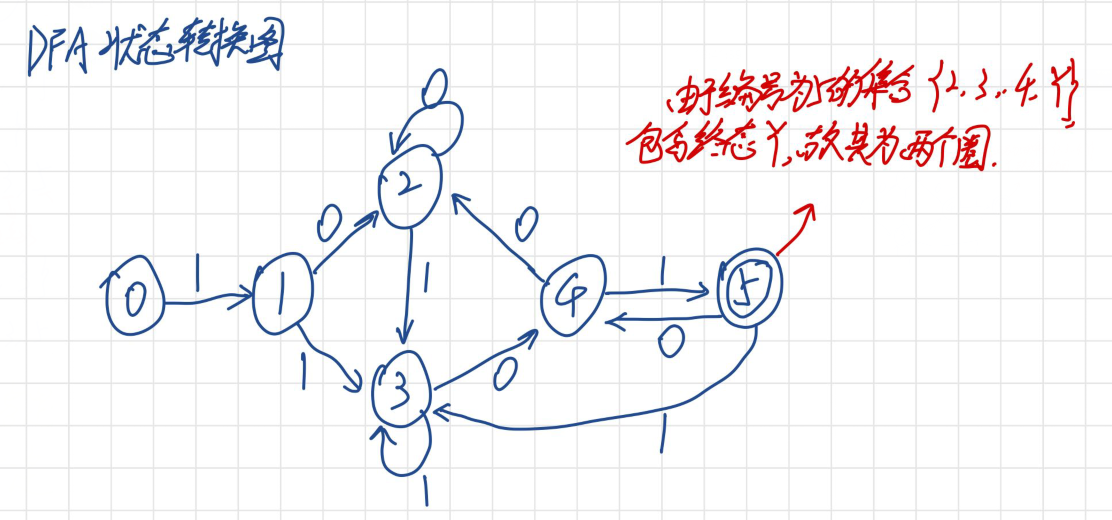
（3）把DFA通过分割法进行化简（最小化）

①最小化的分析过程

我这里刚开始写的比较繁琐，主要是方便理解，做熟悉的话，可以直接写出不成立条件，从集合里拆分出来即可，没必要把成立的也写一遍；这题最终确定的集合为：{0},{1,2},{3},{4},{5}，那么就可以删除一个点 2，因为1可以替代它；

②画出化简后的DFA状态转换图

通过和化简前的对比可以发现，没有删除的点，它都不变；把删除的点的自环传给替代它的点，把2的入边（原来指向2的边，现在指向它的替代，也就是指向1），2的出边（就是由2引出去的边）不用管；

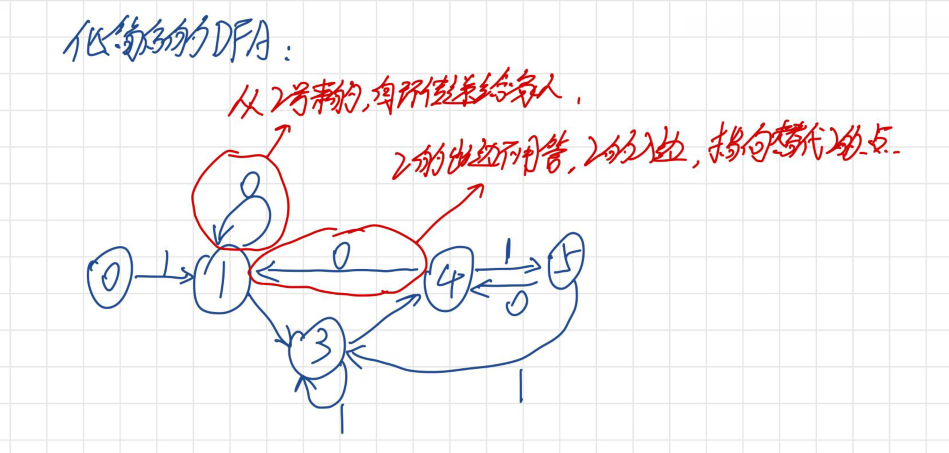
2.通过NFA图构造DFA

这种类型题其实和上面一样，只不过比上面少一步，不需要自己把正规式转化为NFA；

例题

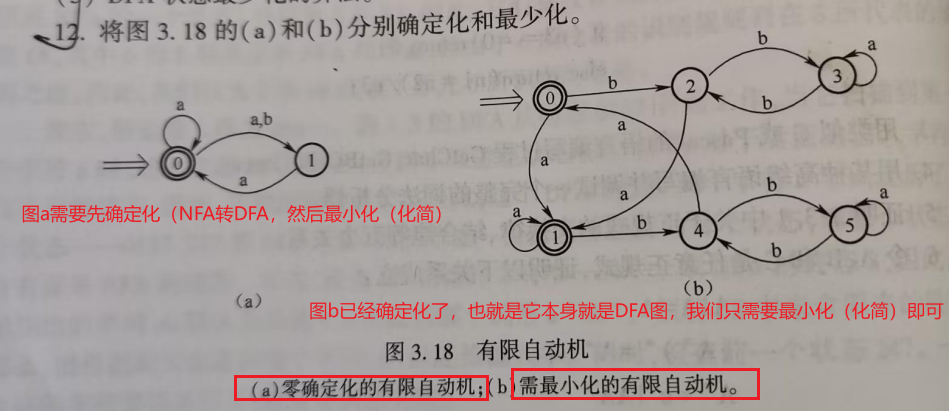
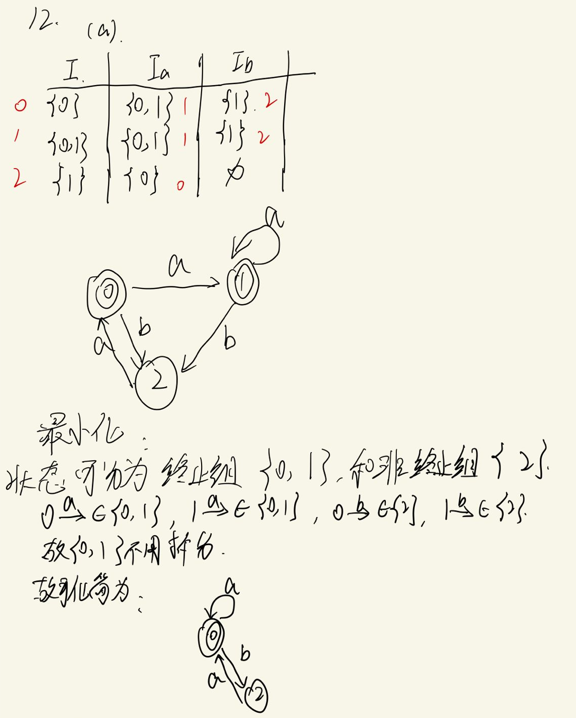
第一问，对于图a，和上面一样，先画出状态转换矩阵，对矩阵进行编号，然后画出DFA，然后通过分割法进行化简，然后画出化简后的DFA即可；

第二问直接分割法化简，然后根据化简结果，删除一些非必要的点画出DFA即可；

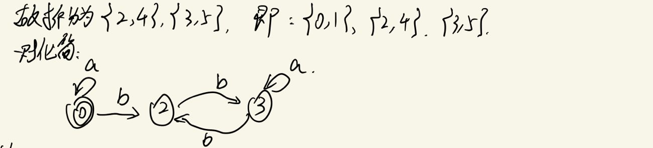
3.需要先求正规式再构造DFA

这种类型题，需要先把题目的描述用正规式表示出来，然后通过上面的步骤进行DFA的求解；

例题

这个符号串是由0和10构成的，所以它的正规式为：(0|10)*，然后这就是第一条的 通过正规式构造DFA，按照上述步骤解决即可；