一、题目描述

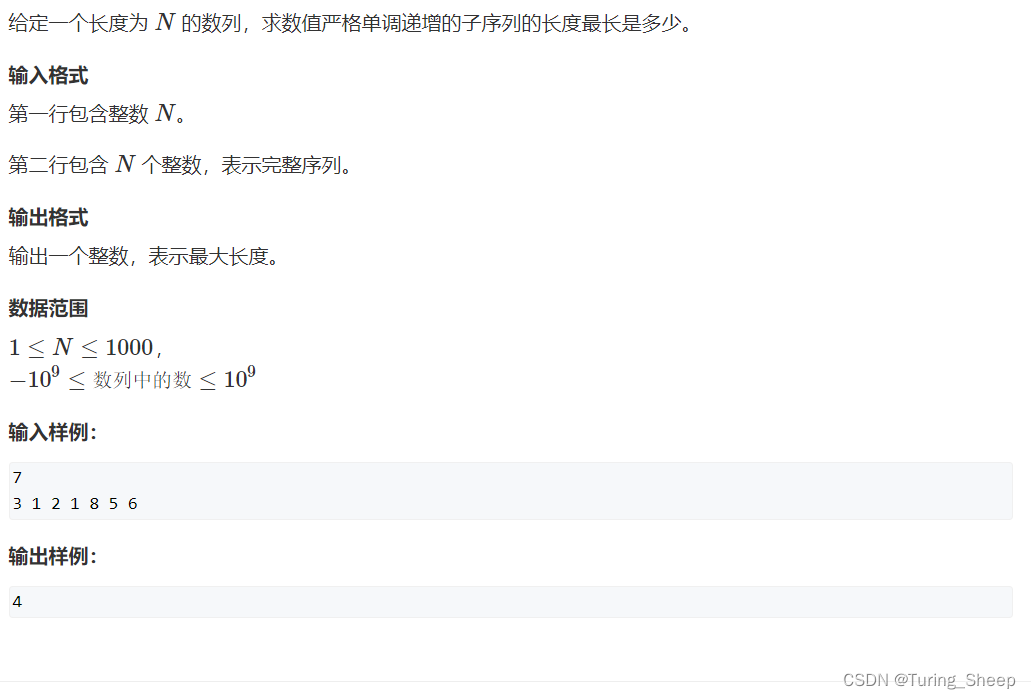
二、思路分析

1、问题分析

其实这道题第一个思路就是深度优先搜索，类似于全排列的感觉，我们只需要不断地枚举出所有的情况比较出最大值即可。但是这样的时间复杂度是非常高的。

那么我们先来思考一下，如何优化？

如果采用DFS的思路来做的话，
$$\begin{gathered} 3,8 \\ 1,2,8 \\ 2,8 \\ 8 \end{gathered}$$
我们可以枚举出上述几个子序列，假设我们在上述子序列的后面继续添加数字的话，我们必须保证我们添加的数字是大于$8$的，因为题目中要求的是最大上升子序列。也就是说，我们的下一位填什么只和当前子序列的最后一位有关系。

那么上述这四个子序列可以归结为一类，即以$8$为结尾的上升子序列。

另外，我们发现，由于最后一位是一样的，所以他们后面所添加的数字很有可能是一样的，我们假设后面补充了相同的$n$个数字，那么现在来看最长的依旧是当前序列中的第二个。

也就是说，在以$8$为结尾的上升子序列中，只有最长的那个子序列才有可能经过后续的补充成为答案。其余情况都不如这个长。所以我们每次只需要去对以某个数$i$结尾的子序列中最长的那个做后续的选择，其余情况不需要枚举。

经过上述的分析，我们得到两点：

1、下一个数字的选择只取决于子序列的最后一位。
2、我们只需要对具有相同最后一位的子序列中最长的子序列去进行后续的操作。

同时我们发现，一个最长子序列中包含很多子问题，因此它满足重叠子问题。其次，我们每次都是让子序列中最长的去继续枚举，也就是说我们每次只用最优解，因此，它符合最优子结构的性质。我们后续的选择，不会影响子问题的结果，因此，它也符合无后效性的性质。

综上，我们可以使用动态规划来解决，而动态规划其实本质上就是对搜索的优化，我们又恰好找到了优化的方法。所以，我们将利用我们刚刚上述的两条结论去写动态规划的代码。

2、思路分析

（1）状态转移方程

状态表示

$f(i)$表示的是以$i$为结尾的子序列中的最长子序列的长度。

状态转移

状态转移就是用小规模的问题去表示大规模的问题。

题目中给定一个序列，我们从左边遍历，也就是说以当前数字$i$左侧的数字结尾的最长子序列就是$f(i)$的子问题。那么我们现在要解决的就是如何用这些子问题去表示$f(i)$，很明显，其实就是看前面的各种子序列中是否能够选上$i$。如果子序列中的最后一个数小于$i$，那么就能够选$i$，此时这个序列的长度也加上了$1$。然后我们在这些序列中取出一个最大值，我们就能找到以$i$为结尾的子序列的最大值。

$$f(i)=max\{\begin{array}{ll}1& 只有i一个元素\\ f(k1)+1& k1<i\\ f(k2)+1& k1<i\\ ...& \\ f(k3)+1& k1<i\end{array}$$

（2）循环设计

循环很简单，就是从左遍历序列即可。

但是我们需要注意的是，我们最终得到的是以序列中不同数字为结尾时，子序列的最大值。但是题目中并没说以哪个数字为结尾，题目只需要一个最大值，因此，需要再在这些以不同数字结尾的子序列的最大值中取出一个最大值。

为了方便，我们将利用数组的下标去写方程。

三、代码实现

#include<iostream>
using namespace std;
const int N=1010;
int dp[N],a[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    
    for(int i=1;i<=n;i++)//从左遍历序列。
    {
        dp[i]=1;//只有一个元素a[i]的时候，子序列的长度为1，我们将其设置为默认值。
        for(int j=1;j<i;j++)//状态转移方程。
        {
           if(a[j]<a[i])
           {
               dp[i]=max(dp[j]+1,dp[i]);
           }
        }
    }
    int res = 0;//再次循环，挑出最大值。
    for (int i = 1; i <= n; i ++ ) res = max(res, dp[i]);
    cout<<res<<endl;
}