基础优化算法
- 梯度下降
- 选择学习率
- 小批量随机梯度下降
- 选择批量大小Batch_size
- 总结
梯度下降
- 挑选一个初始值 w 0 w_0 w0
- 重复迭代参数 t=1,2,3
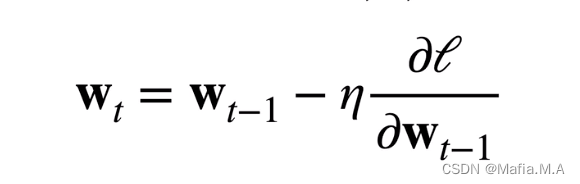
w t w_t wt等于上一个时刻 w t − 1 w_t-1 wt−1减去一个(学习率标量和损失函数关于 w t − 1 w_t-1 wt−1处的梯度) - 沿梯度方向将增加损失函数值
- 学习率:步长的超参数
选择学习率
- 不能太小:每一次走的步长很有限,到达一个点需要走非常多步,计算梯度次数太多(贵)
- 不能太长:步长太大,迈过了梯度下降的地方,使得一直在震荡并没有在下降
小批量随机梯度下降
- 在整个训练集上算梯度太贵(损失函数是对所有样本的统计)
一个深度神经网络模型可能需要数分钟至数小时 - 我们可以随机采样b个样本
i
1
,
i
2
,
.
.
.
,
i
b
i_1,i_2,..., i_b
i1,i2,...,ib来近似损失
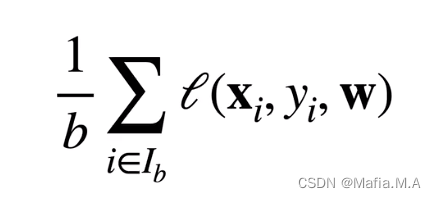
b是批量大小,另一个重要的超参数
选择批量大小Batch_size
- 不能太小:每次计算量太小,不适合并行来最大利用计算资源
- 不能太大:内存消耗增加浪费计算,例如如果所有样本都是相同的
总结
- 梯度下降通过不断沿着反梯度方向更新参数求解
- 小批量随机梯度下降时深度学习默认的求解算法
- 两个重要的超参数是批量大小和学习率
初始化模型参数、定义模型、定义损失函数、定义优化算法、训练
![B树(B-树) [数据结构与算法][Java]](https://img-blog.csdnimg.cn/a02d8fdaaf7c4993900a646268a857a4.png#pic_center)