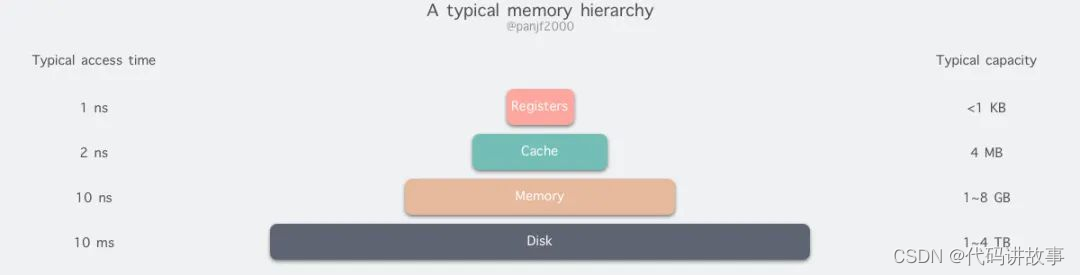
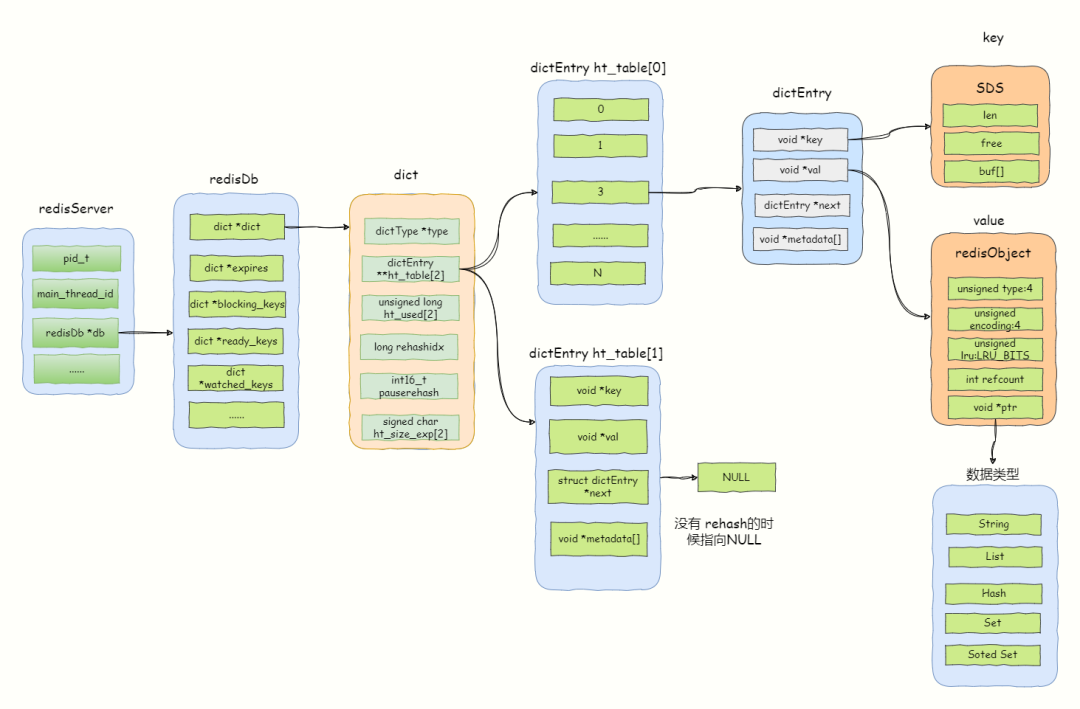
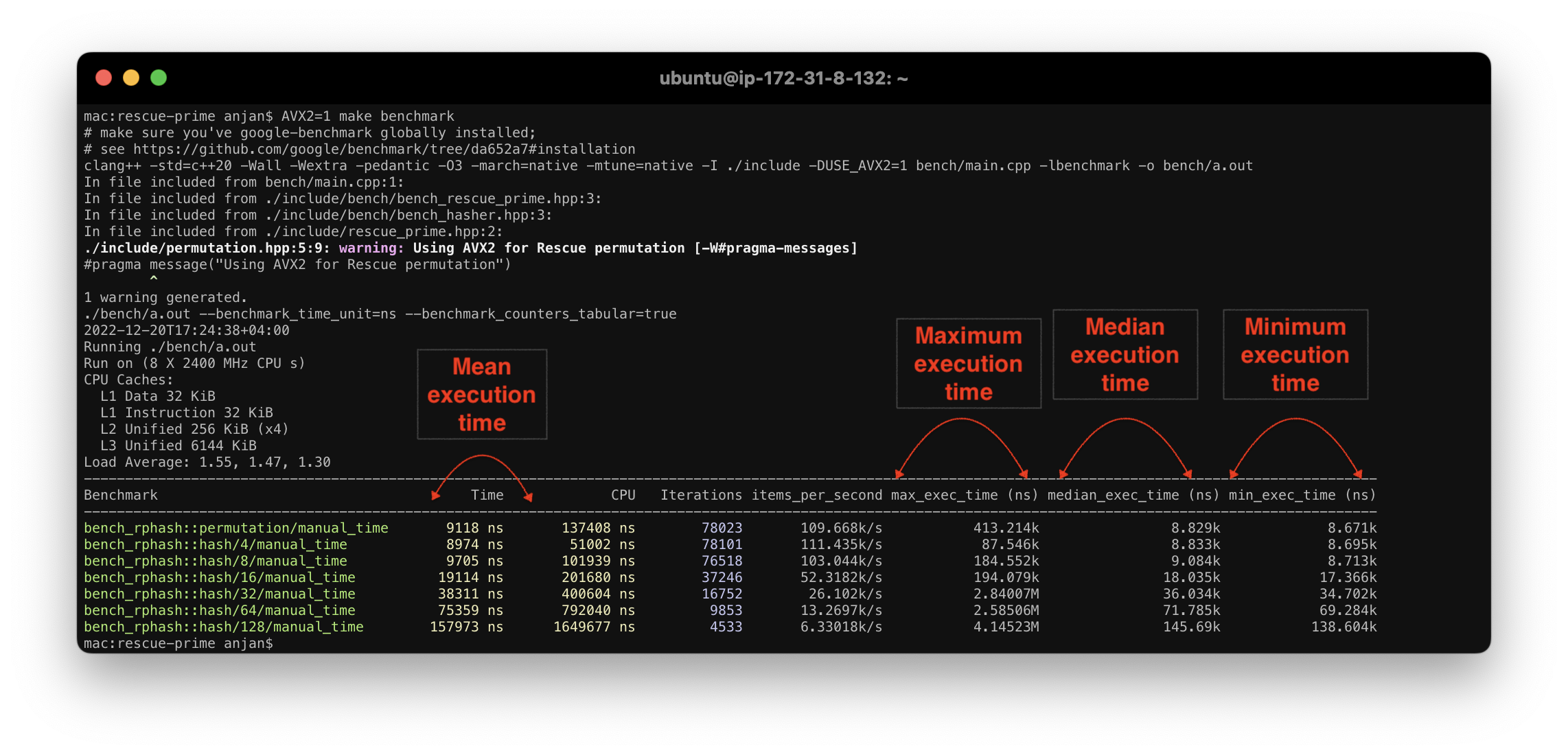
引入
树状数组和线段树具有相似的功能,但他俩毕竟还有一些区别:树状数组能有的操作,线段树一定有;线段树有的操作,树状数组不一定有。但是树状数组的代码要比线段树短,思维更清晰,速度也更快,在解决一些单点修改的问题时,树状数组是不二之选。
过程
下面这张图展示了树状数组的工作原理:
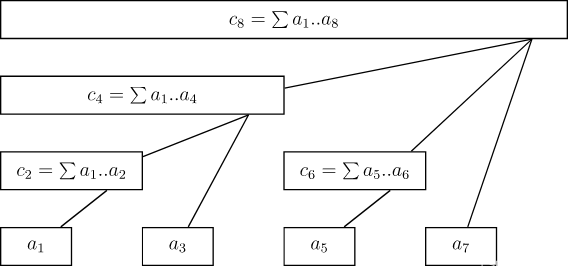
这个结构和线段树有些类似:用一个大节点表示一些小节点的信息,进行查询的时候只需要查询一些大节点而不是所有的小节点。
最上面的八个方块就代表数组 a a a。
他们下面的参差不齐的剩下的方块就代表数组 a a a 的上级—— c c c 数组。
从图中可以看出: 管理的是
c
2
c_2
c2
a
1
a_1
a1,
a
2
a_2
a2;
c
4
c_4
c4 管理的是
a
1
a_1
a1,
a
2
a_2
a2,
a
3
a_3
a3,
a
4
a_4
a4;
c
6
c_6
c6 管理的是
a
5
a_5
a5,
a
6
a_6
a6;
c
8
c_8
c8 则管理全部
8
8
8 个数。
如果要计算数组 a a a 的区间和,比如说要算 a 51 a_{51} a51 ~ a 91 a_{91} a91 的区间和,可以采用类似倍增的思想:
从 91 91 91 开始往前跳,发现 c n c_n cn( n 我也不确定是多少,算起来太麻烦,就意思一下)只管 a 91 a_{91} a91 这个点,那么你就会找 a 90 a_{90} a90 ,发现 c n − 1 c_{n-1} cn−1 管的是 a 90 a_{90} a90& a 89 a_{89} a89;那么你就会直接跳到 a 88 a_{88} a88, c n − 2 c_{n-2} cn−2 就会管 c 81 c_{81} c81~ c 88 c_{88} c88 这些数,下次查询从 a 80 a_{80} a80 往前找,以此类推。
用法及操作
那么问题来了,怎么知道 c i c_i ci 管理的数组 a a a 中的哪个区间呢? 这时,我们引入一个函数——lowbit:
int lowbit(int x) {
// x 的二进制表示中,最低位的 1 的位置。
// lowbit(0b10110000) == 0b00010000
// ~~~^~~~~
// lowbit(0b11100100) == 0b00000100
// ~~~~~^~~
return x & -x;
}
注释说明了 lowbit 的意思,对于
x
=
88
x=88
x=88:
8
8
(
10
)
=
101100
0
(
2
)
88_{(10)}=1011000_{(2)}
88(10)=1011000(2)
发现第一个
1
1
1 以及他后面的
0
0
0 组成的二进制是
1000
1000
1000
100
0
(
2
)
=
8
(
10
)
1000_{(2)}=8_{(10)}
1000(2)=8(10)
1000
1000
1000 对应的十进制是
8
8
8,所以
c
88
c_{88}
c88 一共管理
8
8
8 个
a
a
a 数组中的元素。 事实上,
c
i
c_i
ci 代表的区间就是
[
i
−
l
o
w
b
i
t
(
i
)
+
1
,
i
]
[i-lowbit(i)+1,i]
[i−lowbit(i)+1,i]。
在常见的计算机中,有符号数采用补码表示。在补码表示下,数 x 的相反数 -x = ~x + 1。
使用 lowbit 函数,我们可以实现很多操作,例如单点修改,将 a x a_x ax 加上 k k k,只需要更新 a x a_x ax 的所有上级:
void add(int x, int k) {
while (x <= n) { // 不能越界
c[x] = c[x] + k;
x = x + lowbit(x);
}
}
前缀求和:
int getsum(int x) { // a[1]..a[x]的和
int ans = 0;
while (x >= 1) {
ans = ans + c[x];
x = x - lowbit(x);
}
return ans;
}

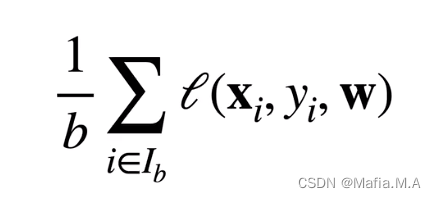
![B树(B-树) [数据结构与算法][Java]](https://img-blog.csdnimg.cn/a02d8fdaaf7c4993900a646268a857a4.png#pic_center)