在安装Homeblew的基础上
替换国内源
export HOMEBREW_API_DOMAIN="https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api"
export HOMEBREW_BREW_GIT_REMOTE="https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git"
brew update
安装Scrcpy
brew install scrcpy
安装adb
brew install android-platform-tools --cask
查看手机的VID,并将VID写入(新建)到~/.android/adb_usb.ini文件中
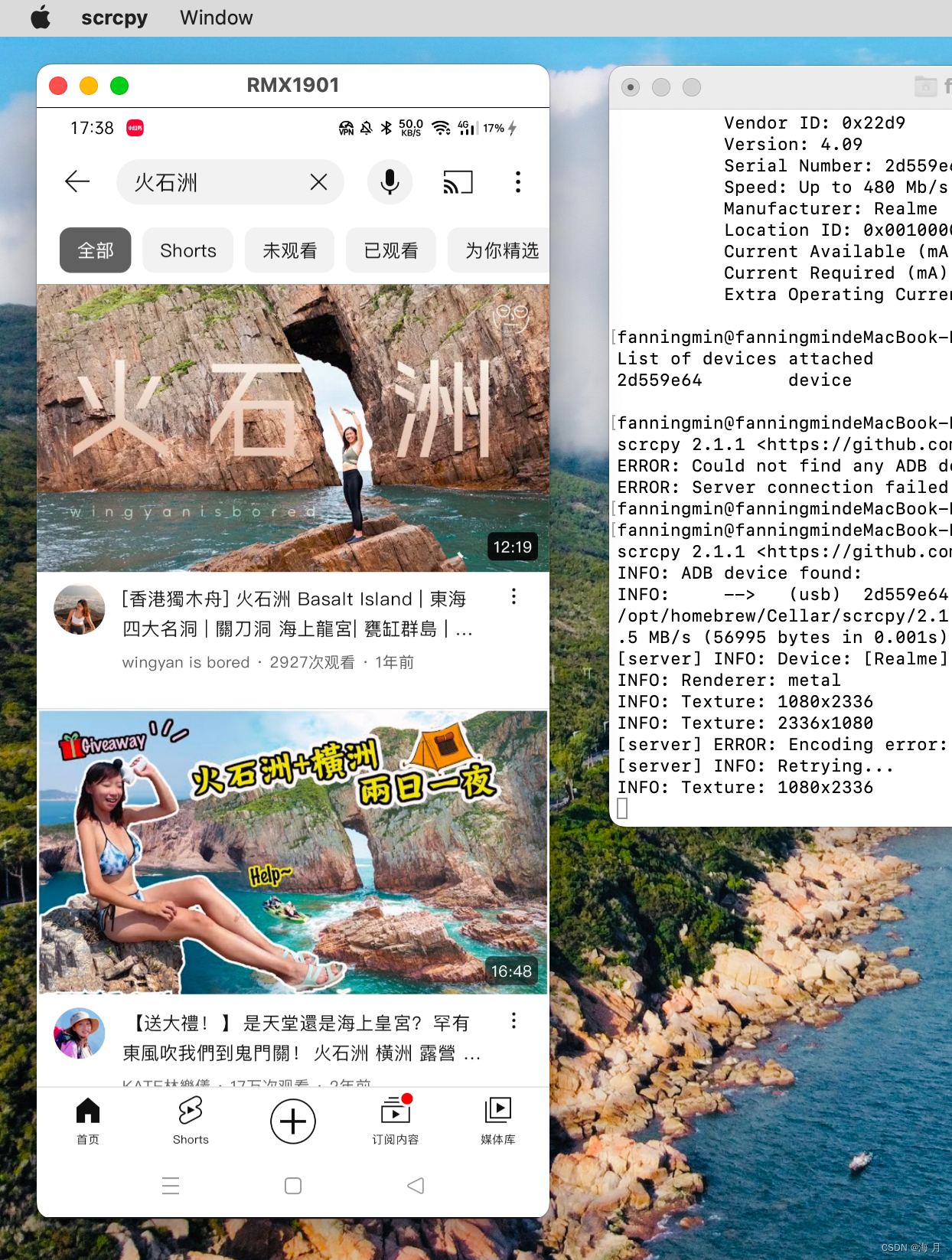
system_profiler SPUSBDataType


adb kill-server 关闭服务
adb start-server 启动服务
adb devices 查看连接状态
![]()
如果找不到设备,在手机设置中:




效果
支持横屏、竖屏




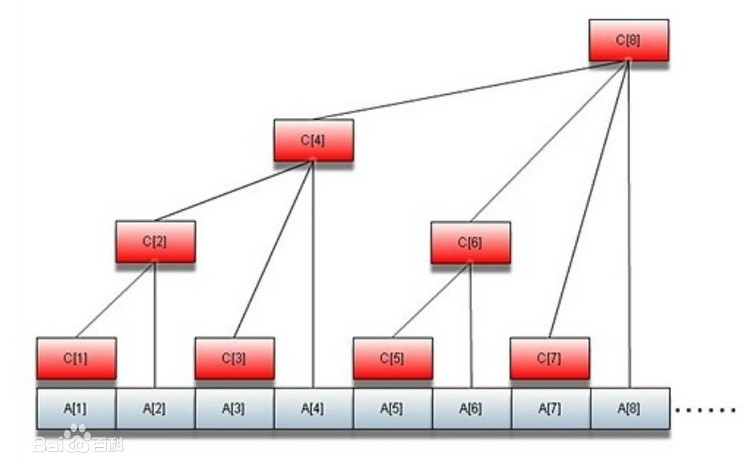
![[swift刷题模板] 树状数组(BIT/FenwickTree)](https://img-blog.csdnimg.cn/854b468cc6e04dfabf15c24059597d91.png)



![[AUTOSAR][网络管理] 什么是BusOff? 如何实现它?](https://img-blog.csdnimg.cn/239a85a05c5646989999126c58a823e7.png#pic_center)