CUDA编程入门系列（十）并行规约

一、什么是规约？

规约，用白话来说，就是将多个值变成一个值的操作，如向量求和，向量内积操作。

以向量求和为例，如果使用串行规约的话，那么就是依靠for循环来进行操作

for(int i = 0; i < nums.size(); i++) sum += nums[i];

但串行规约的话，此时算法的复杂度为O(N).

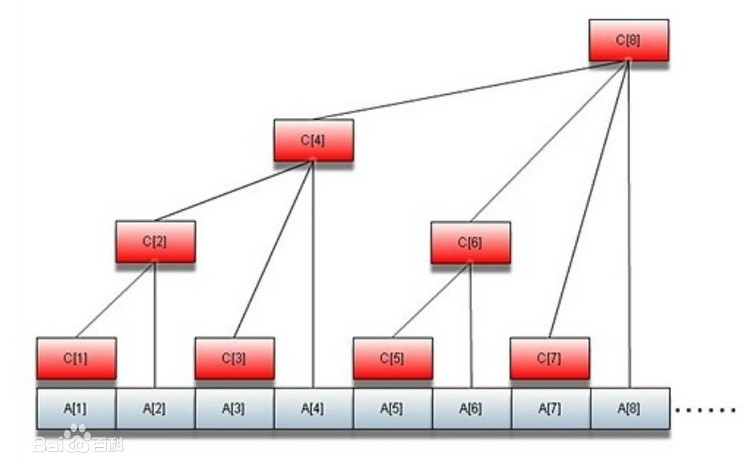
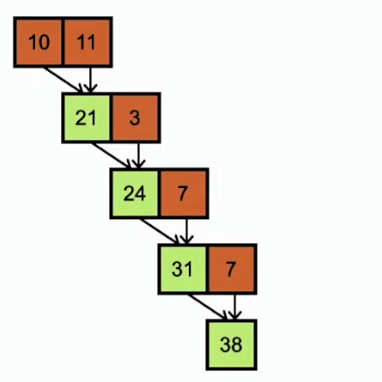
在并行计算中，其中有一种方法叫做二叉树算法，即先将元素两两求和，再进行计算。如下图所示。此时算法的复杂度为O(LogN).

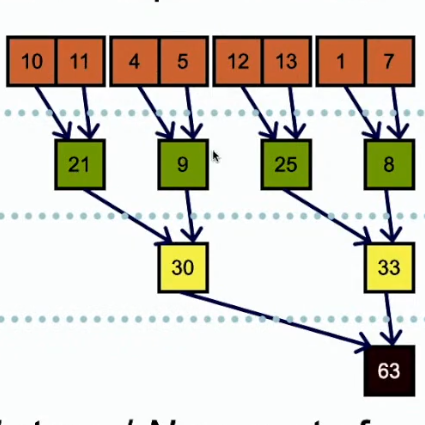
在GPU计算，存在多种策略进行计算。

（1）使用单个block进行计算：不足以充分利用资源

（2）使用多个block进行计算：每个块负责向量的部分计算，再把每个块的计算结果进行处理

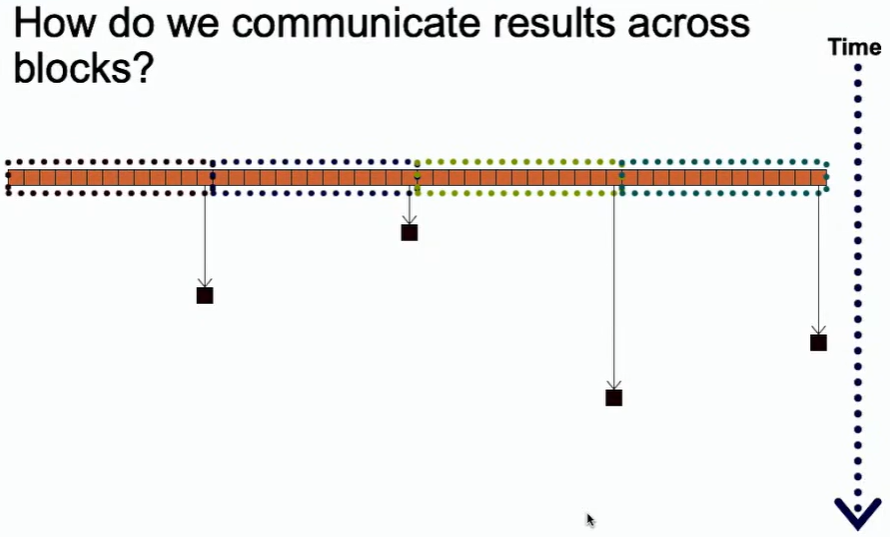
如果使用多个块进行并行规约，那么就可能存在同步问题，不同块的处理规约时间不同。所以，这里的关键就是需要一个全局的同步。

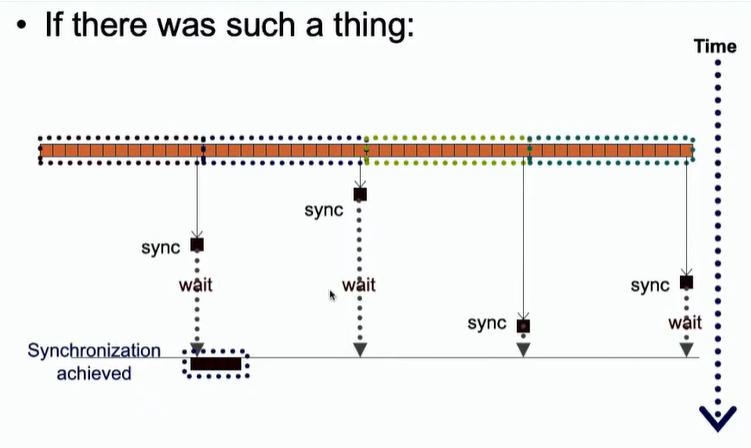
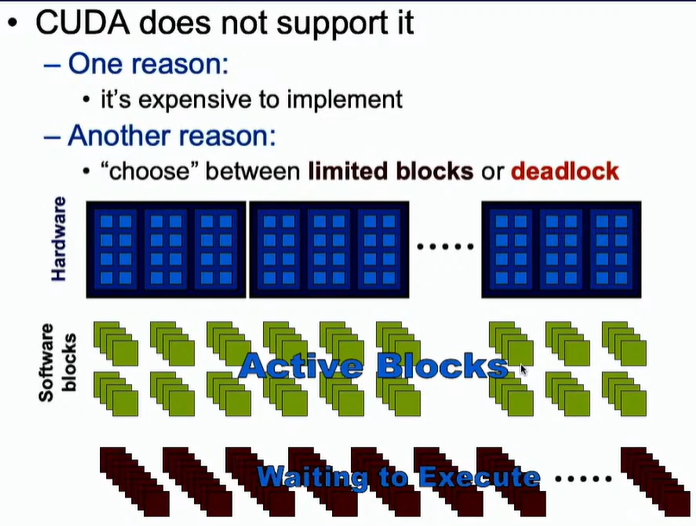
然而，CUDA并不支持全局同步。第一，如果使用全局同步的话，就会使得一些已执行完程序的块处于空闲状态，这会导致资源的浪费。第二，如果使用的块比较多的话，就有可能导致死锁。这里也比较好理解，即大部分的块都申请了SM资源，但不够，所以继续阻塞申请SM资源，也都不释放SM，这就会导致死锁。

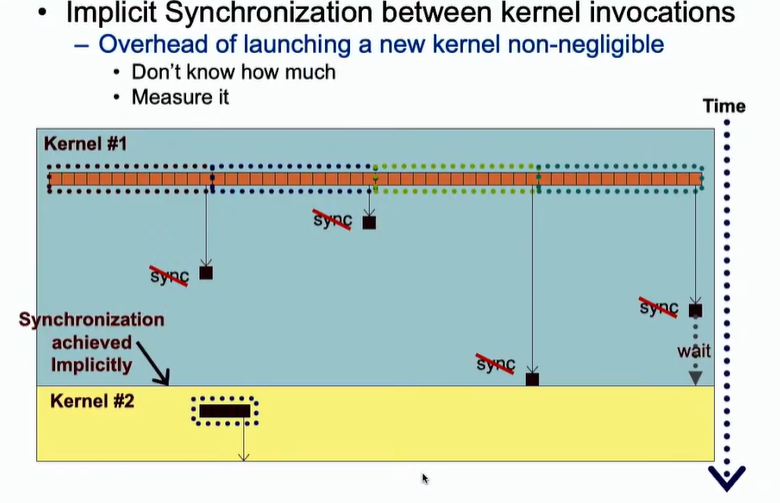
解决方法：分多个kernel进行处理。因为在不同的kenel之间存在隐式的同步，即第一个kernel执行完，才能执行第二个kernel。

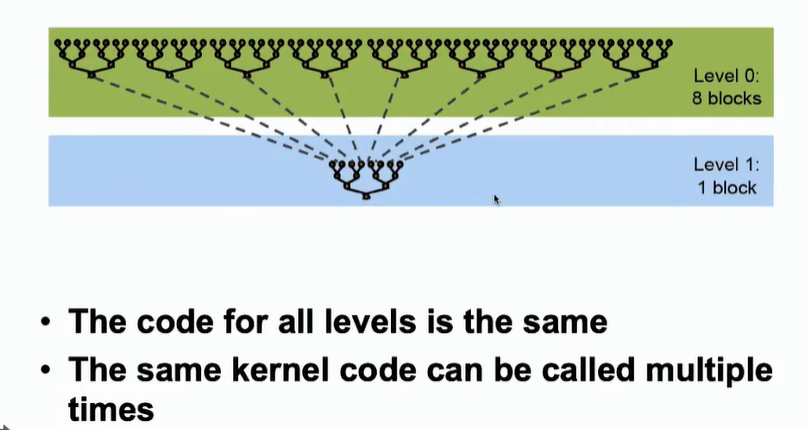
二、并行规约算法 --- 二叉树算法

使用并行规约就是为了最大化GPU的性能，指标包含：浮点运算数GFLOPS和有效带宽GB/s.

二叉树算法，即每两个数相加得到部分和，依次进行该操作，直到最后一个数。步骤如下：

① 将数据从全局内存加载到共享内存当中

② 进行规约操作，每个线程负责规约两个数，每一次规约之后都有一半的线程处于空闲状态。不断进行上述操作，直到只剩下一个线程。

③ 将结果返回到全局内存当中

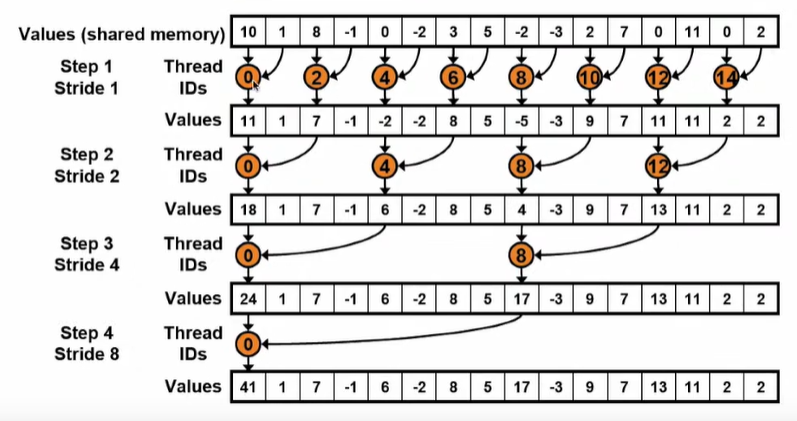
该算法的伪代码如下图所示：

其中 sdata[]代表所申请的共享内存，蓝色方框用以把数据从全局内存拷贝到共享内存。

黄色方框负责进行规约操作，这里只有偶数号线程会进行操作。奇数好线程不操作。这里的__syncthreads()是为了在每一次规约后同步所有线程，直到所有的线程都执行完毕再进行下一次规约。

橘色方框负责将规约结果从共享内存加载到全局内存当中。

消耗时间及带宽如下图所示

因为一个warp里面的32线程执行相同的指令，如果指令不同（即指令分化）的话，可能会导致32个线程按照串行的方式进行执行，这与我们并行的思想是相悖的。所以，这里存在一个问题，因为此处的线程要进行if的分支结构判断，所以就有可能导致不同的线程有不同的指令，导致指令分化，影响执行速度。

如下图所示，绿色方块代表线程处于活跃状态，灰白色方块代表线程处于空闲状态。在同一个warp之内，产生了指令分化。

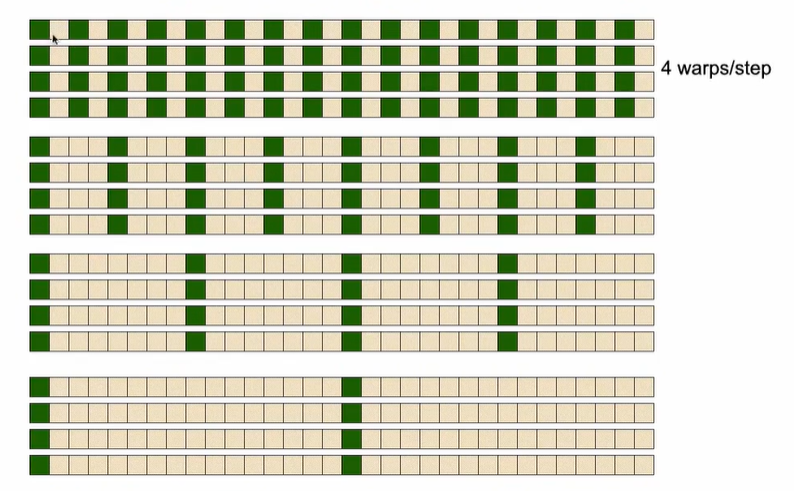
三、并行规约算法改进 warp divergence

由于上述算法存在指令分化问题，会影响执行的速度，所以需要进行改进。改进的思路就是要让一个warp里面的线程执行相同的指令。

改进的方式如黄色框的代码所示，只需要修改三行代码，即可缓解指令分化问题。

通过引入临时变量index，假如s = 1，blockdim=128，那么此时前64个线程都执行相同的指令，后64个线程也执行相同的指令，就避免了指令分化的问题。但是随着计算的进行，s的增大，越来越少的线程处于活跃状态，当活跃的线程小于一个warp的数量的时候，还是会产生指令分化的问题。

改进后的算法，其warp内线程的状态如下图所示：

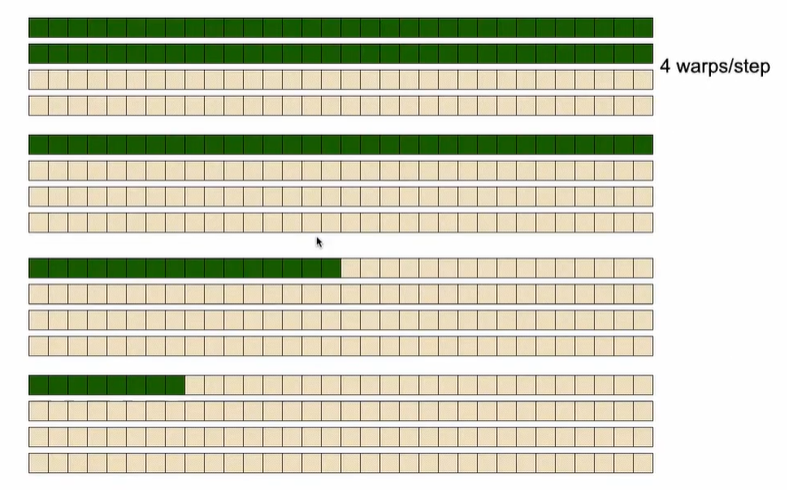
时间和带宽如下所示：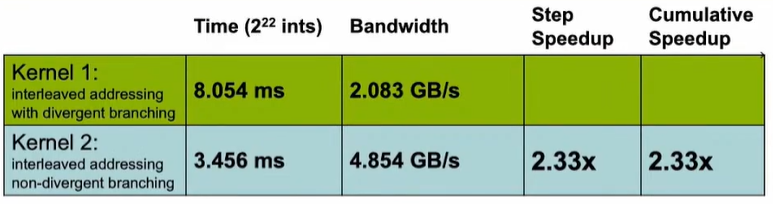

但这里又存在一个问题，会产生bank conflict。通过参考其他博客的内容，bank conflict的含义为：同一个warp中的不同线程，访问相同的bank，就会产生conflict。在这个例子中，其实我没太理解是如何产生冲突的。有一种可能就是比如说线程1 是将第0个数和第1个数进行相加，也就是说线程1要访问第0个数和第1个数，而线程2要访问第1个数和第2个数，这就导致了warp中的不同线程访问了相同的地址。不同的线程访问同一资源，要进行临界操作，由原来的并行操作变成串行操作，影响了执行速度。

四、并行规约算法改进消除bank conflict

在三中，通过不同的编码方式，消除了warp内指令分化的情况。但是也引进了bank conflict问题。bank conflict 会把访问相同bank的线程由并行执行改为串行执行，严重的影响了执行速度。

故而，我们对算法进行如下的改进，我们不再使用相邻数相加的方式，而是采用跳跃的方式进行相加，以”折半“的形式进行相加。每次规约都把后半部分的内容加到前半部分的中。

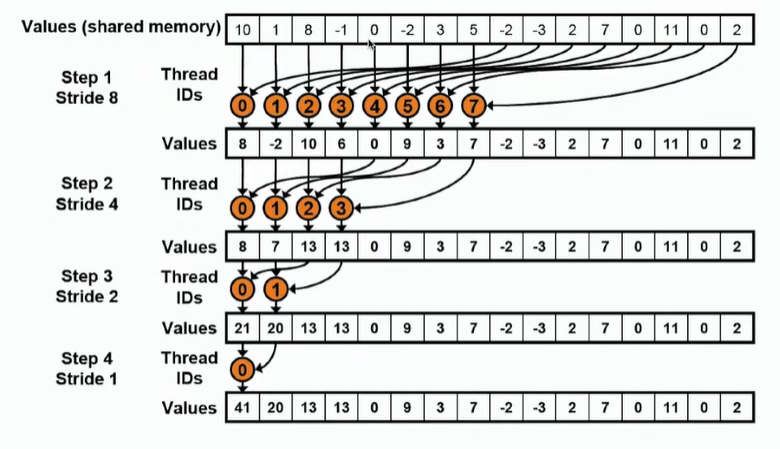
其伪代码如下图所示：

代码的执行速度和带宽如下图所示：

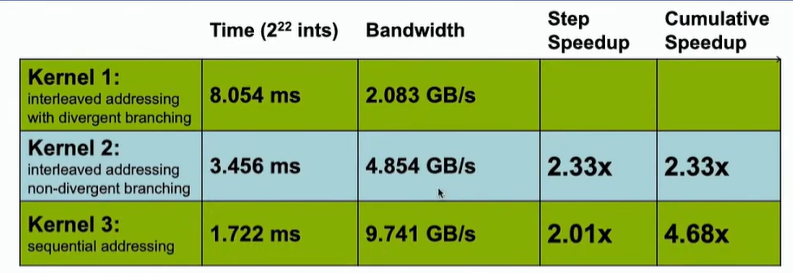
五、并行规约算法改进改进全局内存访问

下图中，橘色方框所示代码为将数据从全局内存加载到共享内存中的方式，每一个线程只加载一个元素。而黄色方框所示代码进行了改进，每一个线程加载两个元素，并且执行了第一步的规约。这就提高了程序的执行速度。但这里？黄色方框写的代码，不会导致g_idata访问越界吗？这里没太懂啊。。。

速度和带宽：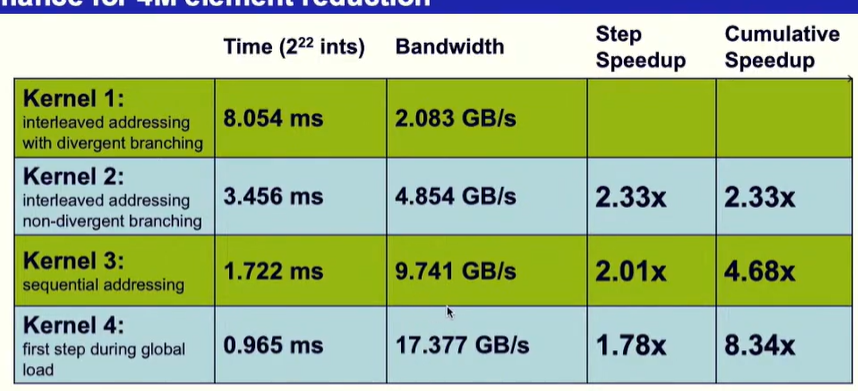

五、并行规约算法改进 warp内循环展开

四种的规约算法代码如下：在每一个步计算中都要使用同步语句来进行同步。

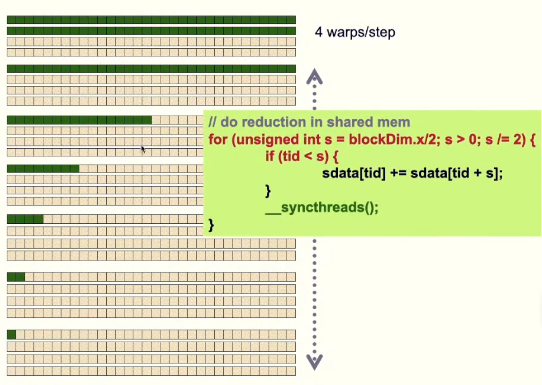
但根据warp的特性，warp内中32个线程会执行相同的指令。那么当活跃的线程数小于32个时，所有的活跃线程都在一个warp内执行相同的指令，因为执行相同的指令，所以这个时候就不需要__syncthreads() 同步点，因此减少开销。改进完的代码如下图所示：在黄色方框所示的代码当中，由于编译器会对代码进行优化，然而，共享内存中的数据是不断进行更新的。所以我们不希望编译器对代码进行优化，所以我们要对共享内存添加关键字volatile。

速度和带宽：

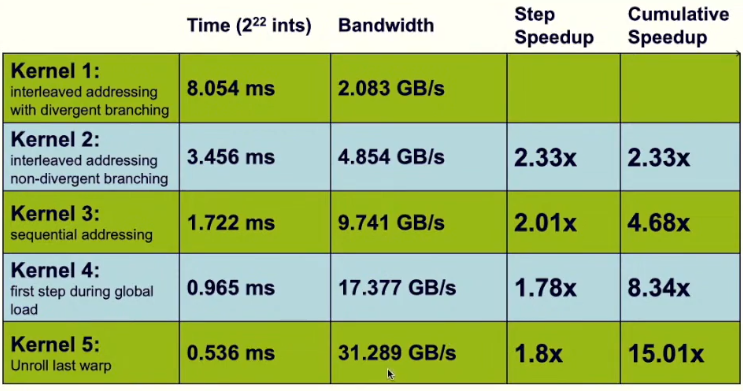
六、并行规约算法改进完全循环展开

在五中，我们对最后几个循环进行展开，减少了同步的次数，以此提高的执行效率。那么，能否将所有的循环全部展开？答案是可以的，但是存在以下前提：每个块中最多只有512个线程，且必须为2的n次方

速度和带宽：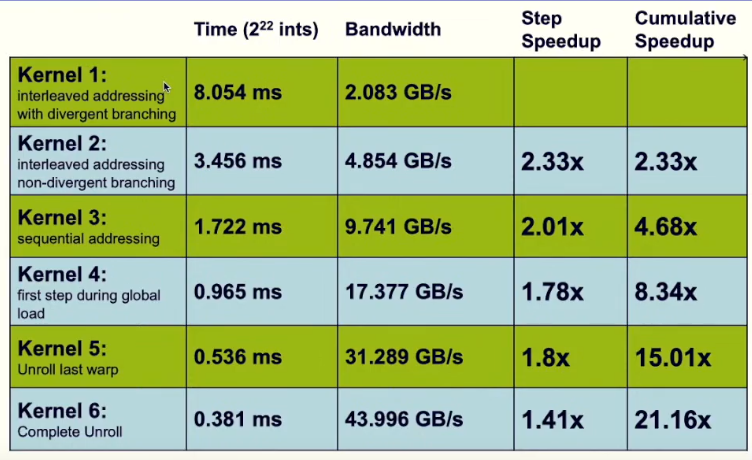

七、规约算法应用：向量内积


/* dot product of two vectors: d = <x, y> */

#include "aux.h"
#include <assert.h>

typedef double FLOAT;

/* host, add */
FLOAT dot_host(FLOAT *x, FLOAT *y, int N)
{
    int i;
    FLOAT t = 0;

    assert(x != NULL);
    assert(y != NULL);

    for (i = 0; i < N; i++) t += x[i] * y[i];

    return t;
}

__device__ void warpReduce(volatile FLOAT *sdata, int tid)
{
    sdata[tid] += sdata[tid + 32];
    sdata[tid] += sdata[tid + 16];
    sdata[tid] += sdata[tid + 8];
    sdata[tid] += sdata[tid + 4];
    sdata[tid] += sdata[tid + 2];
    sdata[tid] += sdata[tid + 1];
}

/* partial dot product */
__global__ void dot_stg_1(const FLOAT *x, FLOAT *y, FLOAT *z, int N)
{
    __shared__ FLOAT sdata[256];
    int idx = get_tid();
    int tid = threadIdx.x;
    int bid = get_bid();

    /* load data to shared mem */
    if (idx < N) {
        sdata[tid] = x[idx] * y[idx];
    }
    else {
        sdata[tid] = 0;
    }

    __syncthreads();

    /* reduction using shared mem */
    if (tid < 128) sdata[tid] += sdata[tid + 128];
    __syncthreads();

    if (tid < 64) sdata[tid] += sdata[tid + 64];
    __syncthreads();

    if (tid < 32) warpReduce(sdata, tid);

    if (tid == 0) z[bid] = sdata[0];
}

/* sum all entries in x and asign to y
 * block dim must be 256 */
__global__ void dot_stg_2(const FLOAT *x, FLOAT *y, int N)
{
    __shared__ FLOAT sdata[256];
    int idx = get_tid();
    int tid = threadIdx.x;
    int bid = get_bid();

    /* load data to shared mem */
    if (idx < N) {
        sdata[tid] = x[idx];
    }
    else {
        sdata[tid] = 0;
    }

    __syncthreads();

    /* reduction using shared mem */
    if (tid < 128) sdata[tid] += sdata[tid + 128];
    __syncthreads();

    if (tid < 64) sdata[tid] += sdata[tid + 64];
    __syncthreads();

    if (tid < 32) warpReduce(sdata, tid);

    if (tid == 0) y[bid] = sdata[0];
}

__global__ void dot_stg_3(FLOAT *x, int N)
{
    __shared__ FLOAT sdata[128];
    int tid = threadIdx.x;
    int i;

    sdata[tid] = 0;

    /* load data to shared mem */
    for (i = 0; i < N; i += 128) {
        if (tid + i < N) sdata[tid] += x[i + tid];
    }

    __syncthreads();

    /* reduction using shared mem */
    if (tid < 64) sdata[tid] = sdata[tid] + sdata[tid + 64];
    __syncthreads();

    if (tid < 32) warpReduce(sdata, tid);

    if (tid == 0) x[0] = sdata[0];
}

/* dz and d serve as cache: result stores in d[0] */
void dot_device(FLOAT *dx, FLOAT *dy, FLOAT *dz, FLOAT *d, int N)
{
    /* 1D block */
    int bs = 256;

    /* 2D grid */
    int s = ceil(sqrt((N + bs - 1.) / bs));
    dim3 grid = dim3(s, s);
    int gs = 0;

    /* stage 1 */
    dot_stg_1<<<grid, bs>>>(dx, dy, dz, N);

    /* stage 2 */
    {
        /* 1D grid */
        int N2 = (N + bs - 1) / bs;

        int s2 = ceil(sqrt((N2 + bs - 1.) / bs));
        dim3 grid2 = dim3(s2, s2);

        dot_stg_2<<<grid2, bs>>>(dz, d, N2);

        /* record gs */
        gs = (N2 + bs - 1.) / bs;
    }

    /* stage 3 */
    dot_stg_3<<<1, 128>>>(d, gs);
}

int main(int argc, char **argv)
{
    int N = 10000070;
    int nbytes = N * sizeof(FLOAT);

    FLOAT *hx = NULL, *hy = NULL;
    FLOAT *dx = NULL, *dy = NULL, *dz = NULL, *d = NULL;
    int i, itr = 20;
    FLOAT asd = 0, ash;
    double td, th;

    if (argc == 2) {
        int an;

        an = atoi(argv[1]);
        if (an > 0) N = an;
    }

    /* allocate GPU mem */
    cudaMalloc((void **)&dx, nbytes);
    cudaMalloc((void **)&dy, nbytes);

    cudaMalloc((void **)&dz, sizeof(FLOAT) * ((N + 255) / 256));
    cudaMalloc((void **)&d, sizeof(FLOAT) * ((N + 255) / 256));

    if (dx == NULL || dy == NULL || dz == NULL || d == NULL) {
        printf("couldn't allocate GPU memory\n");
        return -1;
    }

    printf("allocated %e MB on GPU\n", nbytes / (1024.f * 1024.f));

    /* alllocate CPU mem */
    hx = (FLOAT *) malloc(nbytes);
    hy = (FLOAT *) malloc(nbytes);

    if (hx == NULL || hy == NULL) {
        printf("couldn't allocate CPU memory\n");
        return -2;
    }
    printf("allocated %e MB on CPU\n", nbytes / (1024.f * 1024.f));

    /* init */
    for (i = 0; i < N; i++) {
        hx[i] = 1;
        hy[i] = 2;
    }

    /* copy data to GPU */
    cudaMemcpy(dx, hx, nbytes, cudaMemcpyHostToDevice);
    cudaMemcpy(dy, hy, nbytes, cudaMemcpyHostToDevice);

    /* let dust fall */
    cudaDeviceSynchronize();
    td = get_time();

    /* call GPU */
    for (i = 0; i < itr; i++) dot_device(dx, dy, dz, d, N);

    /* let GPU finish */
    cudaDeviceSynchronize();
    td = get_time() - td;

    th = get_time();
    for (i = 0; i < itr; i++) ash = dot_host(hx, hy, N);
    th = get_time() - th;

    /* copy data from GPU */
    cudaMemcpy(&asd, d, sizeof(FLOAT), cudaMemcpyDeviceToHost);

    printf("dot, answer: %d, calculated by GPU:%f, calculated by CPU:%f\n", 2 * N, asd, ash);
    printf("GPU time: %e, CPU time: %e, speedup: %g\n", td, th, th / td);

    cudaFree(dx);
    cudaFree(dy);
    cudaFree(dz);
    cudaFree(d);

    free(hx);
    free(hy);

    return 0;
}