树状数组

树状数组的用途，主要是可以以 $O(\log n)$ 的时间复杂度维护前缀和。

对于树状数组的使用，我们开一个数组 c，c[x] 表示 $[x-\text{lowbit}(x)+1,x]$ 的区间和。

于是乎，c 数组就构成了这样的结构，我们称 c 为树状数组：

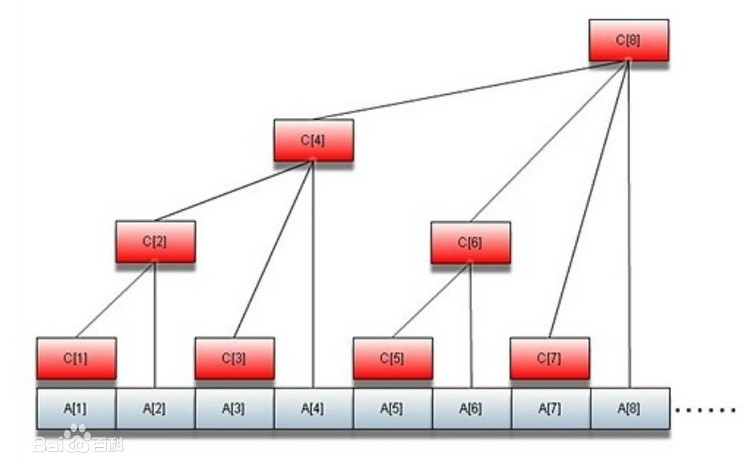
查询 $x$ 的前缀和，代码如下：

int ask(int x)
{
    int res=0;
    while(x) res+=c[x],x-=lowbit(x);
    return res;
}

单点修改，将 $x$ 增加 $v$，代码如下：

void add(int x,int v)
{
    while(x<=n) c[x]+=v,x+=lowbit(x);
    return;
}

---

树状数组 2

重点思想是通过差分把区间修改转化为单点修改。对于要记录的数组 a[i]，假设有 d[i]=a[i]=a[i-1] 且 d[1]=a[1]，那么 a[i] 就等于从 d[1] 到 d[i] 所有元素的和。我们存储的其实是 d 数组的树状数组。如果我们要把从 a[l] 到 a[r] 区间内的所有元素加$1$，其实从 d[l+1] 到 d[r] 都没有变化，只需要 add(l,x)、add(r+1,-x) 即可。

对于单点查询，由 a[i] 等于从 d[1] 到 d[i] 的元素和可知，直接输出前缀和即 ask(i) 即可。

注意，由于这里我们其实是把 a 数组做了一个类似于差分的操作，所以在 add 的时候要加的是当前值与前一位的值的差。

---

二维树状数组

• E. 【例题5】单点修改矩阵查询

  #include <bits/stdc++.h>
  using namespace std;
  typedef long long ll;
  
  const int maxn=5005;
  ll n,m,c[maxn][maxn];
  
  int lowbit(int x){return x&(-x);}
  
  void add(int x,int y,int k)
  {
  	for(int i=x;i<=n;i+=lowbit(i))
  		for(int j=y;j<=m;j+=lowbit(j))
  			c[i][j]+=k;
  }
  
  ll query(int x,int y)
  {
  	ll sum=0;
  	for(int i=x;i;i-=lowbit(i))
  		for(int j=y;j;j-=lowbit(j)) sum+=c[i][j];
  	return sum;
  }
  
  int main()
  {
  	cin>>n>>m;
  	int opt;
  	while(cin>>opt)
  	{
  		if(opt==1) {int x,y,k;cin>>x>>y>>k,add(x,y,k);}
  		else 
  		{
  			int a,b,c,d;cin>>a>>b>>c>>d;
  			cout<<query(c,d)-query(c,b-1)-query(a-1,d)+query(a-1,b-1)<<endl;
  		}
  	}
  	return 0;
  }
  

• F. 【例题6】矩阵修改矩阵查询

  #include<bits/stdc++.h>
  #define inl inline
  #define int long long
  #define ll long long
  
  using namespace std;
  const int N=2e3+50;
  int read()
  {
  	int sum=0,f=1;char c=getchar();
  	while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
  	while(isdigit(c)){sum=(sum<<3)+(sum<<1)+(c^48);c=getchar();}
  	return sum*f;
  }
  
  int lowbit(int x){return x&-x;}
  
  int t[N][N],ti[N][N],tj[N][N],tij[N][N];
  int n,m;
  
  inl void add(int x,int y,int k)
  {
  	for( int i=x;i<=n;i+=lowbit(i))
  		for( int j=y;j<=m;j+=lowbit(j))
          {
  			t[i][j]+=k;
  			ti[i][j]+=x*k;
  			tj[i][j]+=y*k;
  			tij[i][j]+=x*y*k;
  		}
  }
  
  ll query(int x,int y)
  {
  	int ans=0;
  	for( int i=x;i;i-=lowbit(i))
  		for( int j=y;j;j-=lowbit(j))
  			ans+=(x+1)*(y+1)*t[i][j]-ti[i][j]*(y+1)-tj[i][j]*(x+1)+tij[i][j];
  	return ans;
  }
  
  signed main()
  {
  	n=read(),m=read();
  	int opt;
  	while(scanf("%lld",&opt)!=EOF)
      {
  		int x=read(),y=read(),x2=read(),y2=read();
  		if(opt==1)
          {
  			int k=read();
  			add(x,y,k);add(x,y2+1,-k);add(x2+1,y,-k);add(x2+1,y2+1,k);
  		}
  		else
  			printf("%lld\n",query(x2,y2)+query(x-1,y-1)-query(x2,y-1)-query(x-1,y2));
  	}
  	return 0;
  }