题目描述：

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

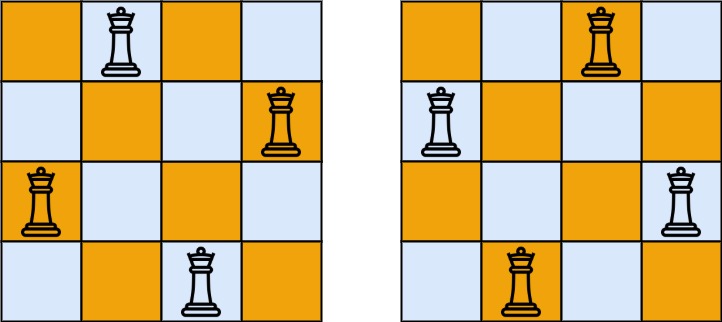
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 9

通过次数

130.8K

提交次数

158.8K

通过率

82.4%

思路和题解：

和第51题一样的思路，只不过是返回每一个解变成了返回解的个数。51：N皇后

通过代码：

class Solution {
public:
    int queen[10];//每一行皇后的位置
    bool attacked(int row,int col)
    {//判断是否被攻击
        for(int i=0;i<row;i++)
        {
            if(col==queen[i]) return true;
            if(row-i==col-queen[i]||row-i==queen[i]-col) return true;
        }
        return false;
    }
    void findspace(int row,int n,int &ans)
    {
        if(row==n)
        {//新的解法
            ans++;
            return ;
        }
        for(int col=0;col<n;col++)
        {
            if(!attacked(row,col))
            {
                queen[row]=col;
                findspace(row+1,n,ans);
                //同一行还有其他解法的时候，queen[row]会被覆盖，所以不需要设queen[row]=0;
            }
        }
    }
    int totalNQueens(int n) {
        memset(queen,0,sizeof(queen));
        int ans=0;
        findspace(0,n,ans);
        return ans;
    }
};