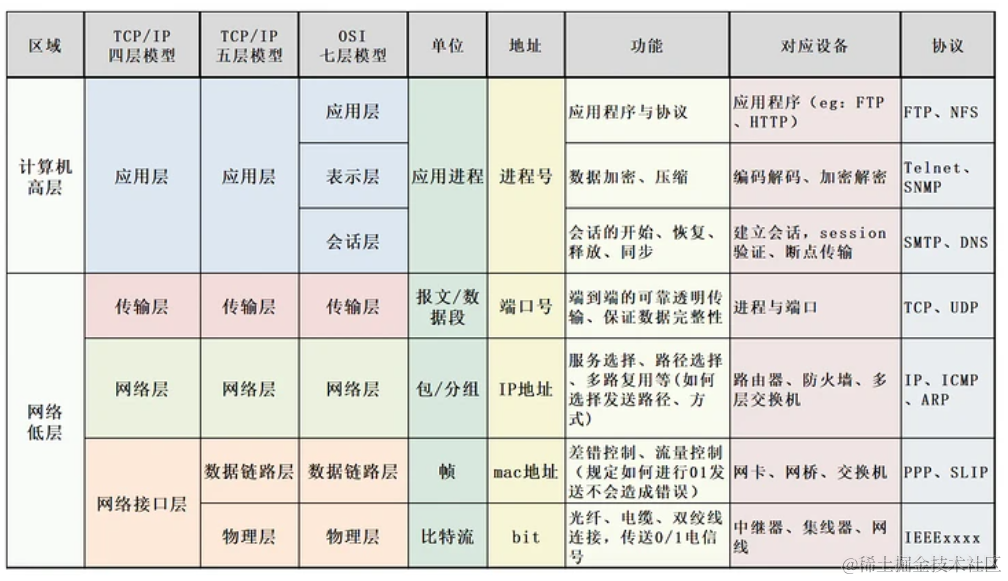
已知 f ( x ) = ln x x f\left(x\right) = \frac{\ln x}{x} f(x)=xlnx,若 f ( x ) = a f\left(x\right) = a f(x)=a有两个不用的零点 x 1 , x 2 x_1, x_2 x1,x2,且 x 1 < x 2 x_1<x_2 x1<x2,求证:
(1)求
a
a
a的范围
f
(
x
)
=
ln
x
x
f\left(x\right)=\frac{\ln x}{x}
f(x)=xlnx
f
′
=
1
−
ln
x
x
2
f^{\prime} = \frac{1-\ln x}{x^2}
f′=x21−lnx
极值点为
x
=
e
x=e
x=e
x
∈
(
0
,
e
)
x\in\left(0,e\right)
x∈(0,e),
f
f
f单调递增
x
∈
(
e
,
+
∞
)
x\in\left(e,+\infty\right)
x∈(e,+∞),
f
f
f单调递减
lim
x
→
0
+
f
(
x
)
=
−
∞
\lim\limits_{x\to 0^+} f\left(x\right) = -\infty
x→0+limf(x)=−∞
lim
x
→
+
∞
f
(
x
)
=
0
\lim\limits_{x\to +\infty} f\left(x\right) = 0
x→+∞limf(x)=0
f
(
e
)
=
1
e
f\left(e\right) = \frac{1}{e}
f(e)=e1
因此
0
<
a
<
1
e
0<a<\frac{1}{e}
0<a<e1
ALG不等式
x
1
x
2
<
x
1
−
x
2
ln
x
1
−
ln
x
2
<
x
1
+
x
2
2
\sqrt{x_1x_2} <\frac{x_1- x_2}{\ln x_1 - \ln x_2}<\frac{x_1+x_2}{2}
x1x2<lnx1−lnx2x1−x2<2x1+x2
x
1
<
e
<
x
2
x_1<e<x_2
x1<e<x2
ln
x
1
=
a
x
1
\ln x_1 = a x_1
lnx1=ax1
ln
x
2
=
a
x
2
\ln x_2 = a x_2
lnx2=ax2
(2) x 1 + x 2 > 2 a x_1+x_2 >\frac{2}{a} x1+x2>a2
x 1 + x 2 > 2 x 1 − x 2 ln x 1 + ln x 2 = 2 a x_1+x_2 > 2 \frac{x_1 - x_2}{\ln x_1 +\ln x_2}=\frac{2}{a} x1+x2>2lnx1+lnx2x1−x2=a2
(3) x 1 + x 2 > 2 e x_1+x_2 > 2e x1+x2>2e
由(2)
x
1
+
x
2
>
2
a
>
2
e
x_1+x_2 >\frac{2}{a}> 2e
x1+x2>a2>2e
(4) x 1 + x 2 > 2 a \sqrt{x_1} + \sqrt{x_2} > \frac{2}{\sqrt{a}} x1+x2>a2
x
1
+
x
2
>
2
x
1
−
x
2
ln
x
1
−
ln
x
2
=
4
a
1
x
1
+
x
2
\sqrt{x_1} + \sqrt{x_2}>2\frac{\sqrt{x_1} - \sqrt{x_2}}{\ln\sqrt{x_1}-\ln\sqrt{x_2}}=\frac{4}{a}\frac{1}{\sqrt{x_1} + \sqrt{x_2}}
x1+x2>2lnx1−lnx2x1−x2=a4x1+x21
因此
x
1
+
x
2
>
4
a
=
2
a
\sqrt{x_1} + \sqrt{x_2}>\sqrt{\frac{4}{a}}=\frac{2}{\sqrt{a}}
x1+x2>a4=a2
(7)
x
1
x
2
<
1
a
2
x_1x_2<\frac{1}{a^2}
x1x2<a21
x
1
x
2
<
x
1
−
x
2
ln
x
1
−
ln
x
2
=
1
a
\sqrt{x1x_2} < \frac{x_1 - x_2}{\ln x_1 - \ln x_2} = \frac{1}{a}
x1x2<lnx1−lnx2x1−x2=a1
因此
x
1
x
2
<
1
a
2
x_1x_2<\frac{1}{a^2}
x1x2<a21
(5) 1 x 1 + 1 x 2 > 2 a \frac{1}{x_1}+\frac{1}{x_2} >2a x11+x21>2a
由(2)和(7)
1
x
1
+
1
x
2
=
x
1
+
x
2
x
1
x
2
>
2
a
a
2
=
2
a
\frac{1}{x_1}+\frac{1}{x_2} = \frac{x_1+x_2}{x_1x_2}>\frac{2}{a}a^2=2a
x11+x21=x1x2x1+x2>a2a2=2a
(6)
e
2
<
x
1
x
2
e^2<x_1x_2
e2<x1x2
由(2)
x
1
x
2
=
e
ln
x
1
+
ln
x
2
=
e
a
(
x
1
+
x
2
)
>
e
a
2
a
=
e
2
x_1x_2 = e^{\ln x_1 + \ln x_2}=e^{a\left(x_1+x_2\right)}>e^{a\frac{2}{a}}=e^2
x1x2=elnx1+lnx2=ea(x1+x2)>eaa2=e2
(9)
x
1
+
x
2
<
−
2
ln
a
a
x_1 +x_2 < \frac{-2\ln a}{a}
x1+x2<a−2lna
由(7)
x
1
+
x
2
=
ln
x
1
+
ln
x
2
a
=
ln
x
1
x
2
a
<
ln
1
a
2
a
=
−
2
ln
a
a
x_1+x_2 = \frac{\ln x_1 + \ln x_2}{a}=\frac{\ln x1_x2}{a}<\frac{\ln \frac{1}{a^2}}{a}=\frac{-2\ln a}{a}
x1+x2=alnx1+lnx2=alnx1x2<alna21=a−2lna
(16)
(
x
1
+
1
)
(
x
2
+
1
)
<
3
a
2
−
2
a
+
1
\left(x_1+1\right)\left(x_2+1\right) <\frac{3}{a^2} -\frac{2}{a}+1
(x1+1)(x2+1)<a23−a2+1
即证明
x
1
+
x
2
+
x
1
x
2
<
3
a
2
−
2
a
=
3
−
2
a
a
2
x_1+x_2 +x_1x_2 < \frac{3}{a^2} -\frac{2}{a}=\frac{3-2a}{a^2}
x1+x2+x1x2<a23−a2=a23−2a
由(9)和(7)
x
1
+
x
2
+
x
1
x
2
<
−
2
ln
a
a
+
1
a
2
=
1
−
2
a
ln
a
a
2
x_1+x_2 +x_1x_2 < \frac{-2\ln a}{a} + \frac{1}{a^2} = \frac{1-2a\ln a}{a^2}
x1+x2+x1x2<a−2lna+a21=a21−2alna
即证明
1
−
2
a
ln
a
<
3
−
2
a
1-2a\ln a <3-2a
1−2alna<3−2a
设
g
(
a
)
=
2
a
ln
a
−
2
a
+
2
(
0
<
a
<
1
e
)
g\left(a\right)=2a\ln a-2a+2\left(0<a<\frac{1}{e}\right)
g(a)=2alna−2a+2(0<a<e1)
g
′
(
a
)
=
2
ln
a
+
2
−
2
=
2
ln
a
<
0
g^{\prime}\left(a\right)=2 \ln a+2-2=2\ln a <0
g′(a)=2lna+2−2=2lna<0
g
(
a
)
>
g
(
1
e
)
=
0
g\left(a\right)>g\left(\frac{1}{e}\right)=0
g(a)>g(e1)=0
因此成立
(25)
f
′
(
x
1
)
+
f
′
(
x
2
)
>
0
f^{\prime}\left(x_1\right) +f^{\prime}\left(x_2\right)>0
f′(x1)+f′(x2)>0
由(5)
f
′
(
x
1
)
+
f
′
(
x
2
)
=
1
−
ln
x
1
x
1
2
+
1
−
ln
x
2
x
2
2
=
1
−
a
x
1
x
1
2
+
1
−
a
x
2
x
2
2
=
1
x
1
2
x
2
2
(
x
1
2
+
x
2
2
−
a
x
1
x
2
(
x
1
+
x
2
)
)
>
1
x
1
2
x
2
2
(
x
1
2
−
x
2
2
ln
x
1
−
ln
x
2
−
a
x
1
x
2
(
x
1
+
x
2
)
)
>
1
x
1
2
x
2
2
(
x
1
2
−
x
2
2
a
x
1
−
a
x
2
−
a
1
a
2
(
x
1
+
x
2
)
)
=
0
\begin{aligned} f^{\prime}\left(x_1\right) +f^{\prime}\left(x_2\right)&=\frac{1-\ln x_1}{x_1^2}+\frac{1-\ln x_2}{x_2^2}\\ &=\frac{1-a x_1}{x_1^2}+\frac{1-a x_2}{x_2^2}\\ &=\frac{1}{x_1^2x_2^2}\left(x_1^2+x_2^2-ax_1x_2\left(x_1+x_2\right)\right)\\ &>\frac{1}{x_1^2x_2^2}\left(\frac{x_1^2-x_2^2}{\ln x_1-\ln x_2}-ax_1x_2\left(x_1+x_2\right)\right)\\ &>\frac{1}{x_1^2x_2^2}\left(\frac{x_1^2-x_2^2}{a x_1-a x_2}-a\frac{1}{a^2}\left(x_1+x_2\right)\right)\\ &=0 \end{aligned}
f′(x1)+f′(x2)=x121−lnx1+x221−lnx2=x121−ax1+x221−ax2=x12x221(x12+x22−ax1x2(x1+x2))>x12x221(lnx1−lnx2x12−x22−ax1x2(x1+x2))>x12x221(ax1−ax2x12−x22−aa21(x1+x2))=0
(29)证明:当 m ≥ 1 m\ge 1 m≥1时, x 1 x 2 m > e m + 1 x_1x_2^m >e^{m+1} x1x2m>em+1
由(6)
x
1
x
2
m
=
x
1
x
2
x
2
m
−
2
>
e
2
e
m
−
2
=
e
m
+
1
x_1 x_2^m =x_1x_2 x_2^{m-2}>e^2 e^{m-2}=e^{m+1}
x1x2m=x1x2x2m−2>e2em−2=em+1
构造函数放缩型[同小]
g
(
x
)
=
ln
x
−
3
x
−
e
x
+
e
g\left(x\right) = \ln x - \frac{3x-e}{x+e}
g(x)=lnx−x+e3x−e
g
′
(
x
)
=
(
x
−
e
)
2
(
x
+
e
)
2
>
0
g^{\prime}\left(x\right) = \frac{\left(x-e\right)^2}{\left(x+e\right)^2}>0
g′(x)=(x+e)2(x−e)2>0
g
(
e
)
=
0
g\left(e\right) = 0
g(e)=0
因此
x
<
e
x<e
x<e时,
ln
x
<
3
x
−
e
x
+
e
\ln x < \frac{3x-e}{x+e}
lnx<x+e3x−e
x
>
e
x>e
x>e时,
ln
x
>
3
x
−
e
x
+
e
\ln x > \frac{3x-e}{x+e}
lnx>x+e3x−e
(12)
3
x
−
e
x
+
e
=
a
x
⇒
a
x
2
+
(
a
e
−
3
)
x
+
e
=
0
\frac{3x-e}{x+e}=ax\Rightarrow ax^2+\left(ae-3\right)x+e=0
x+e3x−e=ax⇒ax2+(ae−3)x+e=0
Δ
=
(
a
e
−
1
)
(
a
e
−
9
)
>
0
\Delta = \left(ae-1\right)\left(ae-9\right)>0
Δ=(ae−1)(ae−9)>0
设
x
3
,
x
4
x_3,x_4
x3,x4为
3
x
−
e
x
+
e
=
a
x
\frac{3x-e}{x+e}=ax
x+e3x−e=ax的两个根
x
3
x
4
=
e
a
x_3x_4 = \frac{e}{a}
x3x4=ae

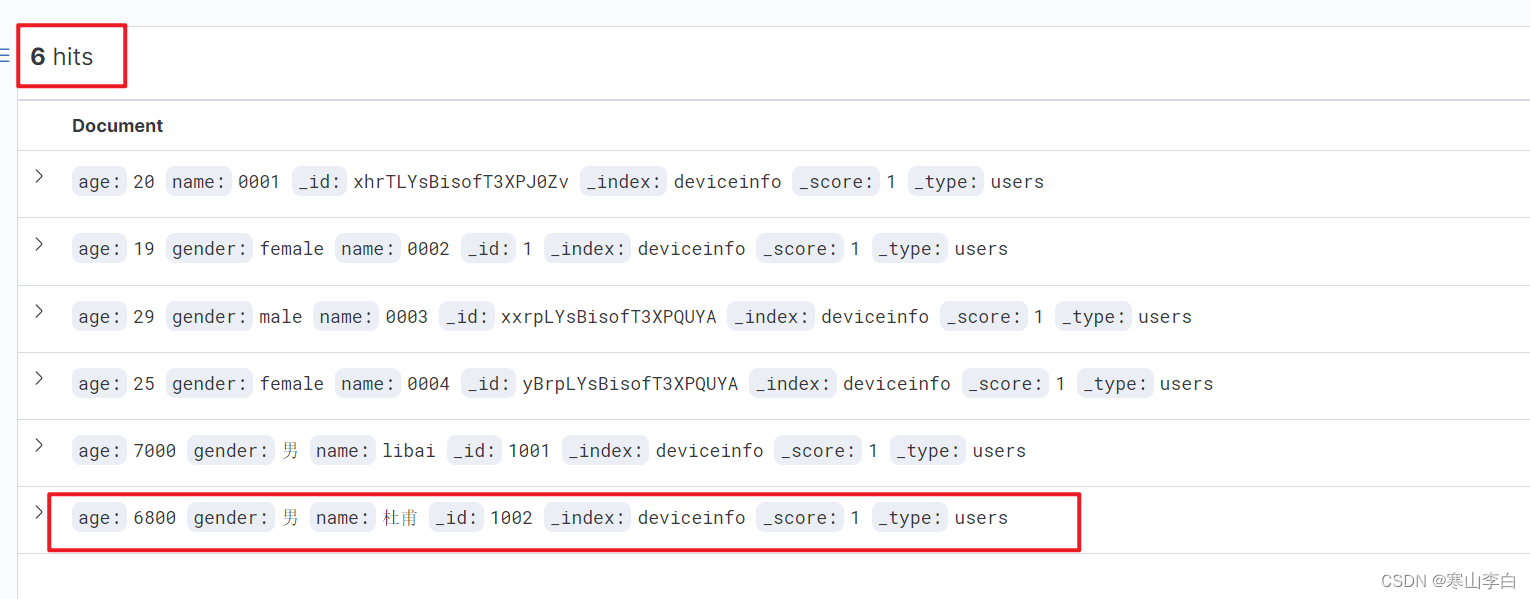
根据图像
x
3
<
x
1
<
e
<
x
2
<
x
4
x_3 < x_1 < e < x_2 < x4
x3<x1<e<x2<x4
因此
x
1
x
2
>
x
3
x
4
=
e
a
x_1 x_2 > x_3 x_4 = \frac{e}{a}
x1x2>x3x4=ae
(11)
ln
x
1
+
ln
x
2
>
1
−
ln
a
\ln x_1 + \ln x_2 >1-\ln a
lnx1+lnx2>1−lna
由(12)
ln
x
1
+
ln
x
2
=
ln
x
1
x
2
>
1
−
ln
a
\ln x_1 +\ln x_2=\ln x_1 x_2 >1-\ln a
lnx1+lnx2=lnx1x2>1−lna
(10)
x
1
+
x
2
>
1
−
ln
a
a
x_1 + x_2 >\frac{1-\ln a}{a}
x1+x2>a1−lna
x
1
+
x
2
=
ln
x
1
+
ln
x
2
a
>
1
−
ln
a
a
x_1 + x_2 =\frac{\ln x_1 +\ln x_2}{a}>\frac{1-\ln a}{a}
x1+x2=alnx1+lnx2>a1−lna
(8)
x
1
+
x
2
>
3
a
−
e
x_1 + x_2 > \frac{3}{a}-e
x1+x2>a3−e
g
(
a
)
=
−
2
−
ln
a
+
e
a
g\left(a\right) = -2-\ln a +ea
g(a)=−2−lna+ea
g
′
(
a
)
=
−
1
a
+
e
<
0
g^{\prime}\left(a\right)=-\frac{1}{a}+e<0
g′(a)=−a1+e<0
g
(
a
)
>
g
(
1
a
)
=
0
g\left(a\right)>g\left(\frac{1}{a}\right)=0
g(a)>g(a1)=0
由(10)
x
1
+
x
2
>
1
−
ln
a
a
>
3
a
−
e
x_1 + x_2 >\frac{1-\ln a}{a}> \frac{3}{a}-e
x1+x2>a1−lna>a3−e
(17)
x
1
2
x
2
+
x
2
2
x
1
>
2
e
a
2
x_1^2 x_2 +x_2^2 x_1 >\frac{2e}{a^2}
x12x2+x22x1>a22e
由(2),(12)
x
1
2
x
2
+
x
2
2
x
1
=
x
1
x
2
(
x
1
+
x
2
)
>
e
a
2
a
=
2
e
a
2
x_1^2 x_2 +x_2^2 x_1=x_1 x_2\left(x_1+x_2\right)>\frac{e}{a}\frac{2}{a}=\frac{2e}{a^2}
x12x2+x22x1=x1x2(x1+x2)>aea2=a22e
构造函数放缩型[同大]
g
(
x
)
=
ln
x
−
x
2
e
+
e
2
x
−
1
g\left(x\right) = \ln x -\frac{x}{2e}+\frac{e}{2x}-1
g(x)=lnx−2ex+2xe−1
g
′
(
x
)
=
−
(
x
−
e
)
2
2
e
x
2
<
0
g^{\prime}\left(x\right) = -\frac{\left(x-e\right)^2}{2ex^2}<0
g′(x)=−2ex2(x−e)2<0
x
<
e
x<e
x<e时,
ln
x
>
x
2
e
−
e
2
x
+
1
\ln x> \frac{x}{2e}-\frac{e}{2x}+1
lnx>2ex−2xe+1
x
>
e
x>e
x>e时,
ln
x
<
x
2
e
−
e
2
x
+
1
\ln x< \frac{x}{2e}-\frac{e}{2x}+1
lnx<2ex−2xe+1
(13) 1 x 1 + 1 x 2 > 2 e \frac{1}{x_1}+\frac{1}{x_2} > \frac{2}{e} x11+x21>e2
x
2
e
−
e
2
x
+
1
=
a
x
⇒
(
2
a
e
−
1
)
x
2
−
2
e
x
+
e
2
=
0
\frac{x}{2e}-\frac{e}{2x}+1 = ax \Rightarrow \left(2ae -1\right)x^2-2ex+e^2=0
2ex−2xe+1=ax⇒(2ae−1)x2−2ex+e2=0
Δ
=
8
e
2
(
1
−
a
e
)
>
0
\Delta=8e^2\left(1-ae\right)>0
Δ=8e2(1−ae)>0
设
x
2
e
−
e
2
x
+
1
=
a
x
\frac{x}{2e}-\frac{e}{2x}+1 = ax
2ex−2xe+1=ax两个根为
x
5
,
x
6
x_5, x_6
x5,x6
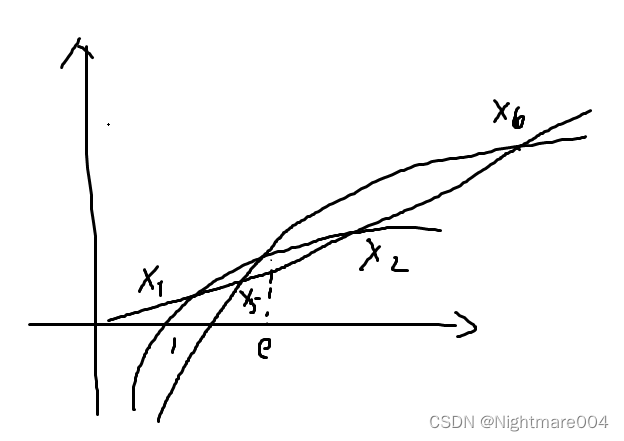
x
1
<
x
5
<
e
<
x
2
<
x
6
x_1 <x_5 < e<x_2 < x_6
x1<x5<e<x2<x6
x
5
+
x
6
=
2
e
2
a
e
−
1
x_5+x_6 = \frac{2e}{2ae-1}
x5+x6=2ae−12e
x
5
x
6
=
e
2
2
a
e
−
1
x_5x_6 = \frac{e^2}{2ae-1}
x5x6=2ae−1e2
1 x 1 + 1 x 2 > 1 x 5 + 1 x 6 = x 5 + x 6 x 5 x 6 = 2 e \frac{1}{x_1}+\frac{1}{x_2} >\frac{1}{x_5}+\frac{1}{x_6}=\frac{x_5+x_6}{x_5x_6}=\frac{2}{e} x11+x21>x51+x61=x5x6x5+x6=e2
(15)
1
ln
x
1
+
1
ln
x
2
>
2
a
e
\frac{1}{\ln x_1} + \frac{1}{\ln x_2} > 2ae
lnx11+lnx21>2ae
由(13)
1
ln
x
1
+
1
ln
x
2
=
1
a
(
1
x
1
+
1
x
2
)
=
2
a
e
>
2
a
e
\frac{1}{\ln x_1} + \frac{1}{\ln x_2}=\frac{1}{a}\left(\frac{1}{x_1}+\frac{1}{x_2}\right)=\frac{2}{ae}>2ae
lnx11+lnx21=a1(x11+x21)=ae2>2ae
构造函数放缩型[间距减小]
g
(
x
)
=
ln
x
−
2
+
e
x
g\left(x\right)=\ln x - 2 +\frac{e}{x}
g(x)=lnx−2+xe
g
′
(
x
)
=
x
−
e
x
2
g^{\prime}\left(x\right)=\frac{x-e}{x^2}
g′(x)=x2x−e
g
(
x
)
≥
g
(
e
)
=
0
g\left(x\right)\ge g\left(e\right)=0
g(x)≥g(e)=0
当且仅当
x
=
e
x=e
x=e时
g
(
x
)
=
0
g\left(x\right)=0
g(x)=0
(19)
x
1
<
1
−
1
−
a
e
a
x_1 < \frac{1-\sqrt{1-ae}}{a}
x1<a1−1−ae
2
−
e
x
=
a
x
⇒
a
x
2
−
2
x
+
e
=
0
2-\frac{e}{x}=ax\Rightarrow ax^2-2x+e=0
2−xe=ax⇒ax2−2x+e=0
Δ
=
4
(
1
−
a
e
)
>
0
\Delta = 4\left(1-ae\right)>0
Δ=4(1−ae)>0
设
2
−
e
x
=
a
x
2-\frac{e}{x}=ax
2−xe=ax的根为
x
7
,
x
8
x_7,x_8
x7,x8
x
7
=
1
−
1
−
a
e
a
,
x
8
=
1
+
1
−
a
e
a
x_7=\frac{1-\sqrt{1-ae}}{a},x_8=\frac{1+\sqrt{1-ae}}{a}
x7=a1−1−ae,x8=a1+1−ae
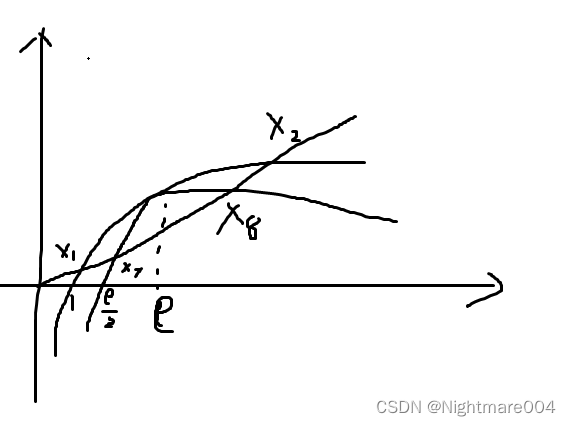
x
1
<
x
7
<
x
8
<
x
2
x_1<x_7<x_8<x_2
x1<x7<x8<x2
因此
x
1
<
1
−
1
−
a
e
a
x_1 < \frac{1-\sqrt{1-ae}}{a}
x1<a1−1−ae
(20)
x
2
>
1
+
1
−
a
e
a
x_2>\frac{1+\sqrt{1-ae}}{a}
x2>a1+1−ae
由(19)成立
(18)
x
1
x
2
<
a
e
\frac{x_1}{x_2}<ae
x2x1<ae
x
1
x
2
<
1
−
1
−
a
e
a
a
1
+
1
−
a
e
=
1
−
1
−
a
e
1
+
1
−
a
e
=
a
e
(
1
+
1
−
a
e
)
2
<
a
e
\frac{x_1}{x_2}<\frac{1-\sqrt{1-ae}}{a}\frac{a}{1+\sqrt{1-ae}}=\frac{1-\sqrt{1-ae}}{1+\sqrt{1-ae}}=\frac{ae}{\left(1+\sqrt{1-ae}\right)^2}<ae
x2x1<a1−1−ae1+1−aea=1+1−ae1−1−ae=(1+1−ae)2ae<ae
(21)
x
2
−
x
1
>
2
1
−
a
e
a
x_2-x_1>\frac{2\sqrt{1-ae}}{a}
x2−x1>a21−ae
由(19),(20)显然
(22)
x
2
−
x
1
>
1
−
a
e
a
x_2-x_1>\frac{\sqrt{1-ae}}{a}
x2−x1>a1−ae
由(21)显然
(23)
x
2
−
x
1
>
1
−
a
e
x_2-x_1>\sqrt{1-ae}
x2−x1>1−ae
由(22)显然
(24)
x
2
−
x
1
>
2
e
a
−
e
2
x_2-x_1>2\sqrt{\frac{e}{a}-e^2}
x2−x1>2ae−e2
由(21)
x
2
−
x
1
>
2
1
−
a
e
a
>
2
e
a
−
e
2
=
2
e
a
1
−
a
e
x_2-x_1>\frac{2\sqrt{1-ae}}{a}>2\sqrt{\frac{e}{a}-e^2}=2\sqrt{\frac{e}{a}}\sqrt{1-ae}
x2−x1>a21−ae>2ae−e2=2ae1−ae
(26) x 2 − x 1 > ( e 2 − 2 ) ( 1 − a e ) x_2-x_1>\left(e^2-2\right)\left(1-ae\right) x2−x1>(e2−2)(1−ae)
e
≈
2.718
e \approx 2.718
e≈2.718
3
≈
1.73
\sqrt{3}\approx 1.73
3≈1.73
因此
e
<
3
+
1
e<\sqrt{3}+1
e<3+1
e
2
−
2
−
2
e
=
(
e
+
3
−
1
)
(
e
−
3
−
1
)
<
0
e^2-2-2e=\left(e+\sqrt{3}-1\right)\left(e-\sqrt{3}-1\right)<0
e2−2−2e=(e+3−1)(e−3−1)<0
由(21)
x
2
−
x
1
>
2
1
−
a
e
a
>
2
e
1
−
a
e
>
(
e
2
−
2
)
1
−
a
e
>
(
e
2
−
2
)
(
1
−
a
e
)
x_2-x_1>\frac{2\sqrt{1-ae}}{a}>2e\sqrt{1-ae}>\left(e^2-2\right)\sqrt{1-ae}>\left(e^2-2\right)\left(1-ae\right)
x2−x1>a21−ae>2e1−ae>(e2−2)1−ae>(e2−2)(1−ae)
(27)
x
2
−
x
1
>
2
(
e
−
2
)
1
−
a
e
x_2-x_1>2\left(e-2\right)\sqrt{1-ae}
x2−x1>2(e−2)1−ae
由(21)
x
2
−
x
1
>
2
1
−
a
e
a
>
2
e
1
−
a
e
>
2
(
e
−
2
)
1
−
a
e
x_2-x_1>\frac{2\sqrt{1-ae}}{a}>2e\sqrt{1-ae}>2\left(e-2\right)\sqrt{1-ae}
x2−x1>a21−ae>2e1−ae>2(e−2)1−ae
切线放缩[间距增大]及特殊非对称式
(28)
x
2
−
x
1
<
4
e
3
2
−
1
−
(
2
e
2
+
1
)
a
(
3
2
e
3
2
<
a
<
1
e
)
x_2-x_1 < 4e^{\frac{3}{2}}-1-\left(2e^2+1\right)a\left(\frac{3}{2e^{\frac{3}{2}}}<a<\frac{1}{e}\right)
x2−x1<4e23−1−(2e2+1)a(2e233<a<e1)
(30)若
1
a
<
(
1
−
m
)
x
1
+
m
x
2
\frac{1}{a}<\left(1-m\right)x_1+m x_2
a1<(1−m)x1+mx2恒成立,求
m
m
m的取值范围
即
m
>
1
a
−
x
1
x
2
−
x
1
m>\frac{\frac{1}{a}-x_1}{x_2-x_1}
m>x2−x1a1−x1
令
s
=
x
2
−
1
a
s=x_2-\frac{1}{a}
s=x2−a1
t
=
1
a
−
x
1
t=\frac{1}{a}-x_1
t=a1−x1
1
a
−
x
1
x
2
−
x
1
=
t
s
+
t
=
1
1
+
s
t
\frac{\frac{1}{a}-x_1}{x_2-x_1}=\frac{t}{s+t}=\frac{1}{1+\frac{s}{t}}
x2−x1a1−x1=s+tt=1+ts1
由(19),(20)
s
t
>
1
+
1
−
a
e
a
−
1
a
1
a
−
1
−
1
−
a
e
a
=
1
\frac{s}{t}>\frac{\frac{1+\sqrt{1-ae}}{a}-\frac{1}{a}}{\frac{1}{a}-\frac{1-\sqrt{1-ae}}{a}}=1
ts>a1−a1−1−aea1+1−ae−a1=1
因此
1
1
+
s
t
<
1
2
\frac{1}{1+\frac{s}{t}}<\frac{1}{2}
1+ts1<21
因此
m
∈
[
1
2
,
+
∞
]
m\in\left[\frac{1}{2},+\infty\right]
m∈[21,+∞]
(14) 2 ln x 1 + ln x 2 > e 2\ln x_1 + \ln x_2 >e 2lnx1+lnx2>e
参考:
https://www.zhihu.com/question/442349127/answer/1711515692