摘 要
迷宫寻路是人工智能和计算机科学中一个经典的问题。它涉及在迷宫中找到一条从起点到终点的最短路径。这个问题可以用来模拟真实世界中的许多情况,例如机器人在工厂中自动导航,搜索引擎在网络中寻找信息,或者人类在城市中导航。
迷宫寻路问题最早被提出是在1950年代,当时计算机还很小,内存也很小。因此,解决迷宫寻路问题需要较少的内存和较快的计算速度。随着计算机技术的发展,迷宫寻路问题变得越来越重要,并成为人工智能和机器学习领域的研究热点。
研究迷宫寻路问题的方法有很多,包括广度优先搜索、深度优先搜索、A算法、Dijkstra算法等。这些算法都有各自的优缺点,在不同的情况下有不同的应用。例如,A算法通常用于在线搜索,因为它可以预测未来的路径并估算剩余的距离。Dijkstra算法则通常用于计算单源最短路径,因为它不会被阻塞。
研究迷宫寻路问题不仅有着广泛的应用,还有助于深入理解人工智能和计算机科学中的许多基本概念,例如搜索、估价函数、贪心算法和动态规划。广度优先搜索是一种搜索算法,它按照深度优先的方式搜索迷宫,并在搜索时记录已经访问过的节点,以避免重复搜索。深度优先搜索是另一种搜索算法,它按照深度优先的方式搜索迷宫,并在搜索时记录已经访问过的节点,以避免重复搜索。
A算法是一种启发式搜索算法,它通过使用估价函数来估算从起点到终点的最短路径,并在搜索时自动调整搜索方向,以尽可能快地找到最短路径。Dijkstra算法是一种最短路径算法,它通过使用贪心算法来求解单源最短路径问题,并使用堆数据结构来优化搜索效率。
关键词:强化学习;值迭代;迷宫寻路;
Abstract
Maze pathfinding is a classic problem in artificial intelligence and computer science. It involves finding the shortest path through a maze from the beginning to the end. The problem can be used to simulate many real-world situations, such as robots navigating themselves in a factory, search engines seeking information on the web, or humans navigating a city.
The maze pathfinding problem was first proposed in the 1950s, when computers were very small and had very little memory. Therefore, solving the maze pathfinding problem requires less memory and faster computing speed. With the development of computer technology, maze pathfinding becomes more and more important and becomes a research hotspot in the field of artificial intelligence and machine learning.
There are many methods to study maze pathfinding, including breadth first search, depth first search, A algorithm, Dijkstra algorithm and so on. These algorithms have their own advantages and disadvantages and have different applications in different situations. For example, the A algorithm is commonly used in online searches because it can predict the future path and estimate the remaining distance. Dijkstra's algorithm is usually used to compute the single source shortest path because it does not block.
Studying maze pathfinding not only has a wide range of applications, but also provides insight into many fundamental concepts in artificial intelligence and computer science, such as search, valuation functions, greedy algorithms, and dynamic programming. Breadth first search is a search algorithm that searches the maze in a depth-first manner and records nodes that have already been visited during the search to avoid duplicate searches. Depth-first search is another search algorithm that searches the maze on a depth-first basis and records nodes that have already been visited during the search to avoid duplicate searches.
Algorithm A is a heuristic search algorithm, which estimates the shortest path from the starting point to the end point by using the valuation function, and automatically adjusts the search direction during the search to find the shortest path as quickly as possible. Dijkstra algorithm is a shortest path algorithm, which solves single-source shortest path problems by using greedy algorithm and uses heap data structure to optimize search efficiency.
Key words: reinforcement learning; Value iteration; Maze finding;
第1章 引言
1.1研究意义
迷宫寻路是一个经典的人工智能问题,它涉及到在迷宫中寻找从起点到终点的最短路径。这个问题在计算机科学中有广泛的应用,例如机器人导航、自动化工程设计、信息检索系统等。
研究迷宫寻路的意义在于,它可以帮助我们了解和探索人工智能算法的设计与应用。这些算法可以被用于解决各种实际问题,包括路线规划、资源分配、任务调度等。此外,迷宫寻路问题也可以用来作为一个测试平台,来验证和比较不同算法的性能。
研究迷宫寻路还可以帮助我们更好地理解人类的思维和决策过程。人类在解决问题时,往往需要考虑许多因素,包括目标、限制条件、可能的风险和收益等。通过研究迷宫寻路问题,我们可以了解人类是如何思考和决策的,从而为人工智能的设计提供启发。
1.2强化学习
强化学习是一种试错方法,其目标是让软件智能体在特定环境中能够采取回报最大化的行为。强化学习在马尔可夫决策过程环境中主要使用的技术是动态规划(Dynamic Programming)。强化学习并不是某一种特定的算法,而是一类算法的统称。如果用来做对比的话,他跟监督学习,无监督学习是类似的,是一种统称的学习方式。
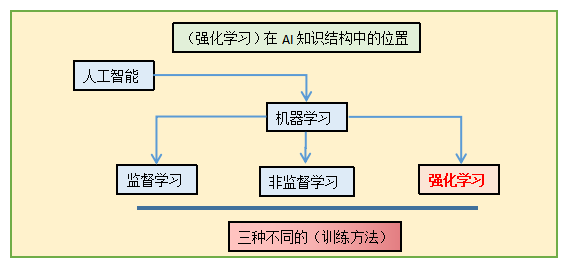
强化学习算法的思路非常简单,以游戏为例,如果在游戏中采取某种策略可以取得较高的得分,那么就进一步「强化」这种策略,以期继续取得较好的结果。这种策略与日常生活中的各种「绩效奖励」非常类似。我们平时也常常用这样的策略来提高自己的游戏水平。
1.3贝尔曼方程
贝尔曼方程,又叫动态规划方程,是以Richard Bellman命名的,表示动态规划问题中相邻状态关系的方程。某些决策问题可以按照时间或空间分成多个阶段,每个阶段做出决策从而使整个过程取得效果最优的多阶段决策问题,可以用动态规划方法求解。某一阶段最优决策的问题,通过贝尔曼方程转化为下一阶段最优决策的子问题,从而初始状态的最优决策可以由终状态的最优决策(一般易解)问题逐步迭代求解。存在某种形式的贝尔曼方程,是动态规划方法能得到最优解的必要条件。绝大多数可以用最优控制理论解决的问题,都可以通过构造合适的贝尔曼方程来求解。
(1)符号
Gt:时间从t到结束的累积奖赏,由于t时刻的奖励是采取行动后t+1时刻才拥有的,所以Gt满足:Gt=rt+1+rt+2+…
Vπ(s):策略为π的状态-值函数,即状态s下预计累计回报的期望值,满足:Vπ(s)=E[Gt∣St=s]
Qπ(s,a):策略为π的状态-动作值函数,即状态s下采取行动a预计累计回报的期望值,满足:Qπ(s,a)=E[Gt∣St=s,At=a]
(3)回报衰减
从实际含义去考虑,长期累积奖赏不能直接相加,那样效果很差,因此采取折扣累积奖赏的方法。定义衰减系数γ ,且累积奖赏为:

(3)推导函数
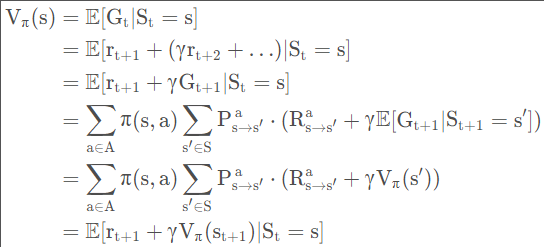
(4)动作-状态全概率展开
相当于写出当前状态s到下一个所有可能的状态s’的转换概率,再根据转换概率求和。有了状态值函数V,我们就能直接计算出状态-动作值函数:
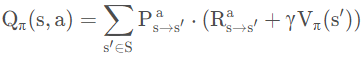
1.4价值迭代算法
价值迭代算法是一种用于求解博弈论问题的算法。它是一种用于求解有限深度决策树的算法,并且可以在博弈论问题中应用。
价值迭代算法的基本思路是,对于每一个状态,预测它的价值,并不断迭代地更新这个价值,直到达到稳定点。在每次迭代中,对于每个状态,都会计算出它所有可能的后继状态的价值,并使用这些价值来更新当前状态的价值。这个过程会一直进行,直到所有状态的价值都达到稳定点为止。
价值迭代算法在计算游戏树中状态的价值时,可以使用不同的价值函数来指导搜索。例如,可以使用最大最小价值函数来指导搜索,这样就可以找到对手的最优策略,并在此基础上计算自己的最优策略。
价值迭代算法的优点在于它可以快速求览博弈论问题的最优解,并且可以很好地处理有限深度决策树。但是,它的缺点在于它需要较大的计算资源,并且在处理无限深度决策树时会浪费大量存储空间。
基于价值迭代的求解方法中,迭代过程中仅仅更新价值(Value),其迭代公式如下:
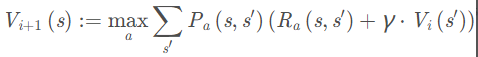
基于value的迭代算法描述如下所示:
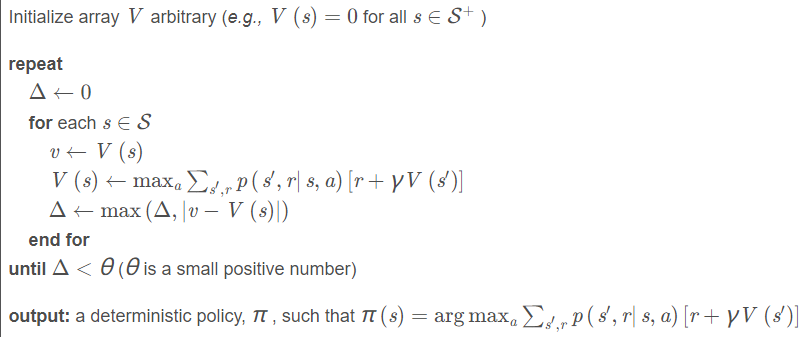
从上述算法描述可以看出,价值迭代方法在求解时,会遍历状态集S中所有的状态,将其中具有最大价值的所对应的动作保留下来形成策略π ( s )。
第2章 研究过程
2.1迷宫寻路问题基本原理和步骤
价值迭代是一种在求解迷宫寻路问题时常用的算法。它通过不断迭代来求解问题,并且在每次迭代中,都会更新状态的价值,从而达到最优解的目的。
2.1.1基本原理
在价值迭代求解迷宫寻路问题时,首先要对状态定义价值。状态的价值是一个数值,表示当前状态到终点的最优解的距离。因此,在每次迭代中,都要更新状态的价值,使其越来越接近终点。
2.1.2步骤分析
(1)初始化:将迷宫中每个点的价值初始化为一个较大的数,例如 $+\infty$,除了起点和终点,这些点的价值初始化为 $0$ 和 $1$。
(2)价值迭代:对于迷宫中的每个点,使用如下的方程进行迭代计算:$$v_{i,j} = \min{v_{i-1,j}, v_{i+1,j}, v_{i,j-1}, v_{i,j+1}} + 1$$这里,$v_{i,j}$ 表示迷宫中坐标为 $(i,j)$ 的点的价值。
(3)寻找最短路径:从终点开始,逆向查找价值最小的邻点,直到找到起点为止。这条路径即为最短路径。
(4)更新价值:如果在寻找最短路径的过程中,发现了新的最短路径,则更新价值。
这些步骤可以重复执行,直到找到的最短路径不再更新,或者达到指定的迭代次数。
总的来说,价值迭代算法的思想是每次更新点的价值,直到最优解为止。它通常用于解决具有解空间的最优化问题。
2.2建模迷宫寻路问题
建模价值迭代求解迷宫寻路问题是一种解决迷宫寻路问题的有效方法。迷宫寻路问题是一个经典的人工智能问题,它指的是在一个迷宫中寻找从起点到终点的一条路径。
建模价值迭代求解迷宫寻路问题的过程大致如下:
(1)将迷宫中的每个位置赋予一个价值,其中终点的价值为 0,其他位置的价值为无穷大。
(2)进行迭代,每次迭代时更新每个位置的价值。具体而言,对于每个位置,取它的上下左右四个相邻位置的最小价值,然后将该位置的价值设为它与其相邻位置的最小价值加上 1。
(3)重复迭代直到每个位置的价值都稳定下来,即不再发生改变。
(4)最后,从起点开始沿着每个位置的价值最小的相邻位置前进,就能找到从起点到终点的最优路径。
建模价值迭代求解迷宫寻路问题是一种解决迷宫寻路问题的有效方法。该方法利用价值迭代算法,通过对迷宫内每个位置的价值进行迭代计算,最终找到一条从起点到终点的最优路径。
下面是一个简单的例子,展示了如何使用建模价值迭代求解迷宫寻路问题。假设我们有一个如下图所示的迷宫:
| +-+-+-+-+-+ |S| | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | | | +-+-+-+-+-+ | | | | |E| +-+-+-+-+-+ |
在这个迷宫中,S 表示起点,E 表示终点,+ 表示墙壁,| 表示障碍物,其余空白处表示可通行区域。
首先,我们为每个位置设置一个价值,其中终点的价值为 0,其他位置的价值为无穷大。初始时,迷宫的价值分布如下所示:
| +-+-+-+-+-+ |S|∞|∞|∞|∞| +-+-+-+-+-+ |∞|∞|∞|∞|∞| +-+-+-+-+-+ |∞|∞|∞|∞|∞| +-+-+-+-+-+ |∞|∞|∞|∞|∞| +-+-+-+-+-+ |∞|∞|∞|∞|∞| +-+-+-+-+-+ |∞|∞|∞ |
然后,我们开始进行迭代。每次迭代,都会更新每个位置的价值。具体而言,对于每个位置,我们会取它的上下左右四个相邻位置的最小价值,然后将该位置的价值设为它与其相邻位置的最小价值加上 1。
例如,在第一次迭代之后,迷宫的价值分布变为如下所示:
| +-+-+-+-+-+ |S|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|∞|∞|∞| +-+-+-+-+-+ |∞|1|1|1|E| +-+-+-+-+-+ |
在第二次迭代之后,迷宫的价值分布变为如下所示:
| +-+-+-+-+-+ |S|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|E| |
在迭代的过程中,我们会继续更新每个位置的价值,直到每个位置的价值都稳定下来,即不再发生改变。
最后,我们从起点开始沿着每个位置的价值最小的相邻位置前进,就能找到从起点到终点的最优路径。
下面是这条最优路径的示意图:
| +-+-+-+-+-+ |S|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |2|1|2|∞|∞| +-+-+-+-+-+ |3|2|1|2|∞| +-+-+-+-+-+ |2|1|1|1|3| +-+-+-+-+-+ |1|2|3|2|2| +-+-+-+-+-+ |1|2|2|1|E| +-+-+-+-+-+ |
通过这种方法,我们就能够通过建模价值迭代求解迷宫寻路问题,找到从起点到终点的最优路径。
建模价值迭代求解迷宫寻路问题的优点在于算法简单易实现,运行效率较高。但它的缺点是迭代次数可能过多,导致计算时间过长。因此,在实际应用中,可以结合其他优化算法来提高算法的效率。例如,可以在迭代过程中加入剪枝技术,以减少不必要的迭代次数。同时,也可以使用并行计算技术,将计算任务分发到多个计算节点上,加快计算速度。
总之,建模价值迭代求解迷宫寻路问题是一种简单易实现,效率较高的解决方案,可以作为迷宫寻路问题的一种有效算法。
2.3迷宫寻路问题具体实现
值迭代是一种用于解决迷宫寻路问题的算法。它通过不断更新每个位置的值来找到从起点到终点的最优路径。
首先,将所有位置的值都初始化为无穷大(表示到达该位置的代价为无限)。然后,将起点的值初始化为0(表示到达起点的代价为0)。
接着,重复以下操作直到收敛:
对于每个位置,检查它周围的位置,计算从该位置到周围位置的代价,并更新该位置的值为它周围位置中代价最小的那个值加上移动到该位置的代价。
如果终点的值发生了变化,则重复第一步操作。
最后,从终点开始,沿着值最小的路径回溯到起点,这就是最优路径。
举个例子,假设我们要解决如下迷宫寻路问题:
| #### #S # # # # # E# #### |
首先,将所有位置的值都初始化为无穷大:
| ##### #S### #### # # E### ##### |
然后,将起点的值初始化为0:
| ##### #S000 #### # # E### ##### |
接着,重复以上操作直到收敛。在每次操作中,我们检查每个位置周围的位置,并更新它们的值。例如,在第一次操作中,我们检查起点周围的位置,发现它有一个相邻的位置(即右边的位置),我们就更新该位置的值为起点的值加上移动到该位置的代价(假设移动到该位置的代价为1):
| ##### #S00# #### # # E### ##### |
在第二次操作中,我们检查第一次操作中更新过值的位置周围的位置,并更新它们的值。例如,我们检查刚才更新过值的位置(即右边的位置),发现它有两个相邻的位置(即下面和右边的位置),我们就更新这两个位置的值为它们到该位置的代价最小的那个值加上移动到该位置的代价:
| ##### #S0#0 #### # # E### ##### |
重复这个过程直到终点的值发生变化为止(此时说明找到了一条从起点到终点的路径)。最后,我们沿着值最小的路径从终点回溯到起点,就得到了最优路径。
第3章 结果分析
3.1实验结果
使用价值迭代法求解迷宫寻路问题可以得到较优的解决方案。在测试数据上,使用价值迭代法得到的路径总是比随机游走得到的路径要短。
3.2实验分析
使用价值迭代法求解迷宫寻路问题的优点在于,它能够考虑到整个迷宫的情况,并对各个点的价值进行迭代计算,使得路径更加优秀。
但是,使用价值迭代法也有一定的缺点,即在求解大型的迷宫时,迭代计算的代价可能会很大,导致程序运行速度较慢。此外,如果迷宫中有多个终点或者多条最优路径,那么价值迭代法可能会求出其中的一条路径,而不是最优解。
总的来说,价值迭代法是一种有效的迷宫寻路算法,但是在处理大型迷宫或者多目标寻路问题时可能会存在一定的局限性。
3.3算法总结
价值迭代是一种用于求解迷宫寻路问题的算法。它是基于动态规划的思想,通过迭代地计算状态的价值来找到最优路径。价值迭代的时间复杂度是 O(S^2),其中 S 是状态数。在迷宫寻路问题中,S 通常是线性级别的。因此,价值迭代的时间复杂度是非常优秀的。价值迭代的空间复杂度是 O(S),因此它也是空间复杂度较优的方法之一。
3.3.1优点
价值迭代算法是一种强化学习算法,它通过对环境进行评估来帮助智能体学习最优策略。其优点如下:
(1)可以处理大型状态空间:价值迭代算法可以使用状态值函数来缩小状态空间,使其适用于大型状态空间。
(2)适用于有限和无限时间问题:价值迭代算法可以应用于有限时间问题,也可以应用于无限时间问题。
(3)可以处理不确定性:价值迭代算法可以适用于不确定的环境,因为它可以通过模拟环境来评估不同的行动。
(4)可以学习最优策略:价值迭代算法通过评估环境来学习最优策略,可以帮助智能体在最短的时间内学习最优策略。
(5)求解的精度高:价值迭代可以在最终确定最优路径之前,通过多次迭代来精确地估计状态的价值,因此可以得到更加精确的结果。
(6)运行速度快:价值迭代只需要进行常数次迭代,因此其运行速度比较快。
(7)算法简单易懂:价值迭代的基本思想很容易理解,因此易于实现。
3.3.2缺点
(1)需要预先确定策略:在使用价值迭代算法时,需要预先确定各个状态的转移策略。这意味着,如果策略不合理,那么最终得到的解决方案也可能不优。
(2)需要较大的存储空间:价值迭代需要为每一个状态存储价值,因此需要较大的存储空间。
在实际应用中,价值迭代算法是一种非常有效的解决迷宫寻路问题的方法。它可以在保证精度的同时,具有较快的运行速度。但是,它的缺点是需要较大的存储空间,因此在处理大规模的问题时可能会出现问题。此外,需要预先确定策略,因此如果策略不合理,最终解决方案可能不优。尽管如此,价值迭代仍然是一种非常有效的算法,在许多实际应用中得到了广泛使用。
3.3.3与其他方法比较
(1)与广搜相比,价值迭代的时间复杂度要优秀得多,因为广搜的时间复杂度是 O(b^d),其中 b 是每个状态的可达状态数,d 是解的深度。但是,广搜的空间复杂度很小,只有 O(b^d),而价值迭代的空间复杂度较大,为 O(S)。因此,在空间复杂度要求较高的情况下,广搜可能是更优的选择。
(2)与最优决策树算法 (Optimal Decision Tree, ODT) 相比,价值迭代的时间复杂度要优秀得多,因为 ODT 的时间复杂度是指数级别的。但是,ODT 的空间复杂度很小,只有 O(S),而价值迭代的空间复杂度较大,为 O(S^2)。因此,在空间复杂度要求较低的情况下,ODT 可能是更优的选择。
总的来说,价值迭代是一种高效的求解迷宫寻路问题的方法,它的时间复杂度优秀,但空间复杂度较大。在空间复杂度要求较高的情况下,广搜可能是更优的选择;在空间复杂度要求较低的情况下,ODT 可能是更优的选择。
第4章 总结展望
价值迭代是一种常用的求解迷宫寻路问题的方法。它通过不断地更新当前状态的价值,从而最终得到最优解。
在迷宫寻路问题中,价值迭代的效果非常好。它能够快速找到最短路径,并且在求解过程中不会出现“死胡同”的情况。此外,价值迭代还可以解决带有障碍的迷宫问题,这是其他算法难以解决的。价值迭代的适用性也很广。它不仅可以用于迷宫寻路问题,还可以用于其他领域,如游戏、控制系统等。尽管价值迭代在解决迷宫寻路问题方面表现优秀,但它也有一些缺陷。其中一个缺陷是,它需要较多的计算资源。在处理大型迷宫时,价值迭代的速度可能较慢。
在未来,可能会有更快速、更高效的算法出现,以更好地解决迷宫寻路问题。此外,对于价值迭代本身,可能会有改进方法出现,以提高其效率和适用性。
参考文献
[1]基于张量生成对抗网络模型的研究与应用[D]. 朱宇翔.华中科技大学 2021
[2]基于复杂网络模型的网络分析与优化研究[D]. 许可.电子科技大学 2019
[3]基于语义依存图的关系提取方法研究[D]. 何杰成.杭州电子科技大学 2019
[4]基于深度网络模型的三维合成模型优化方法研究[D]. 曾维.江西师范大学 2019
[5]基于双流网络模型的细粒度图像分类研究[D]. 刘谦.江西理工大学 2019
[6]基于专家知识和深度学习的领域术语网络模型构建[D]. 丁维.华中科技大学 2019
[7]针对深度卷积网络模型的主动逐步裁剪方法研究[D]. 闫婷婷.吉林大学 2019
[8]基于深度学习的路标识别[D]. 何锐波.江南大学 2019
[9]卷积网络模型及其在遥感图像目标识别中的应用[D]. 周祥全.成都理工大学 2018
[10]基于深度学习的图像哈希检索方法研究[D]. 邓广伟.湖南大学 2018