回归算法

线性回归

• 求解线性回归方法
  • 正规方程
  • 梯度下降
    • 迭代

API

• sklearn.linear_model.LinearRegression

  • 正规方程优化
  • fit_intercept 是否计算偏置量，没有的化经过原点
  • 属性
    • coef_ 回归系数
    • intercept_ 偏置量

• sklearn.linear_model.SGDRegressor

  • 使用随机梯度下降优化
  • 参数
    • loss
      • 损失函数，默认=‘squared_error’，还有huber，epsilon_insensitive，squared_epsilon_insensitive
    • learning_rate
      • 学习率的算法，默认invscaling，
      • constant $\eta ={\eta }_0$
      • optimal $\eta =1.0/(\alpha \ast (t+t_0))$
      • invscaling $\eta ={\eta }_0/t^{powe{r}_t}$
      • adaptive

代码示例

波士顿房价预测

• LinearRegression

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt 

data = load_boston()

x_train,x_test,y_train,y_test = train_test_split(data.data,data.target)
transfer = StandardScaler()

#数据标准化
x_train=transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

reg = LinearRegression()
#使用LinearRegression
reg.fit(x_train,y_train)

print(reg.coef_,reg.intercept_)
y_predict = reg.predict(x_test)

print(y_test)
print(y_predict)

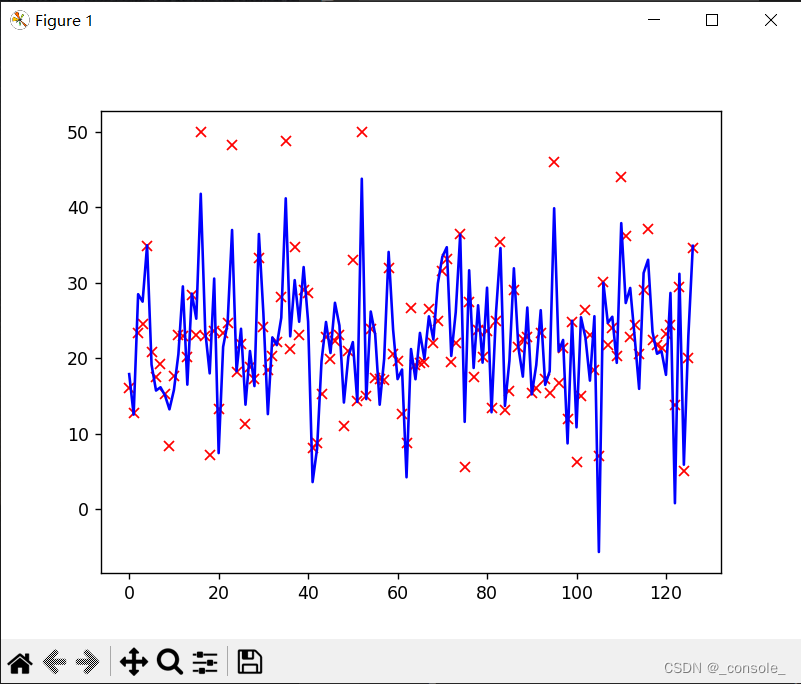
#绘图显示差异
x = list(range(len(y_test)))
plt.plot(x,y_test,'rx')
plt.plot(x,y_predict,'b-')
plt.show()

• SGDRegressor

from sklearn.linear_model import SGDRegressor
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt 

data = load_boston()

x_train,x_test,y_train,y_test = train_test_split(data.data,data.target)
transfer = StandardScaler()

#数据标准化
x_train=transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

reg = SGDRegressor()
#SGDRegressor
reg.fit(x_train,y_train)

print(reg.coef_,reg.intercept_)
y_predict = reg.predict(x_test)

print(y_test)
print(y_predict)

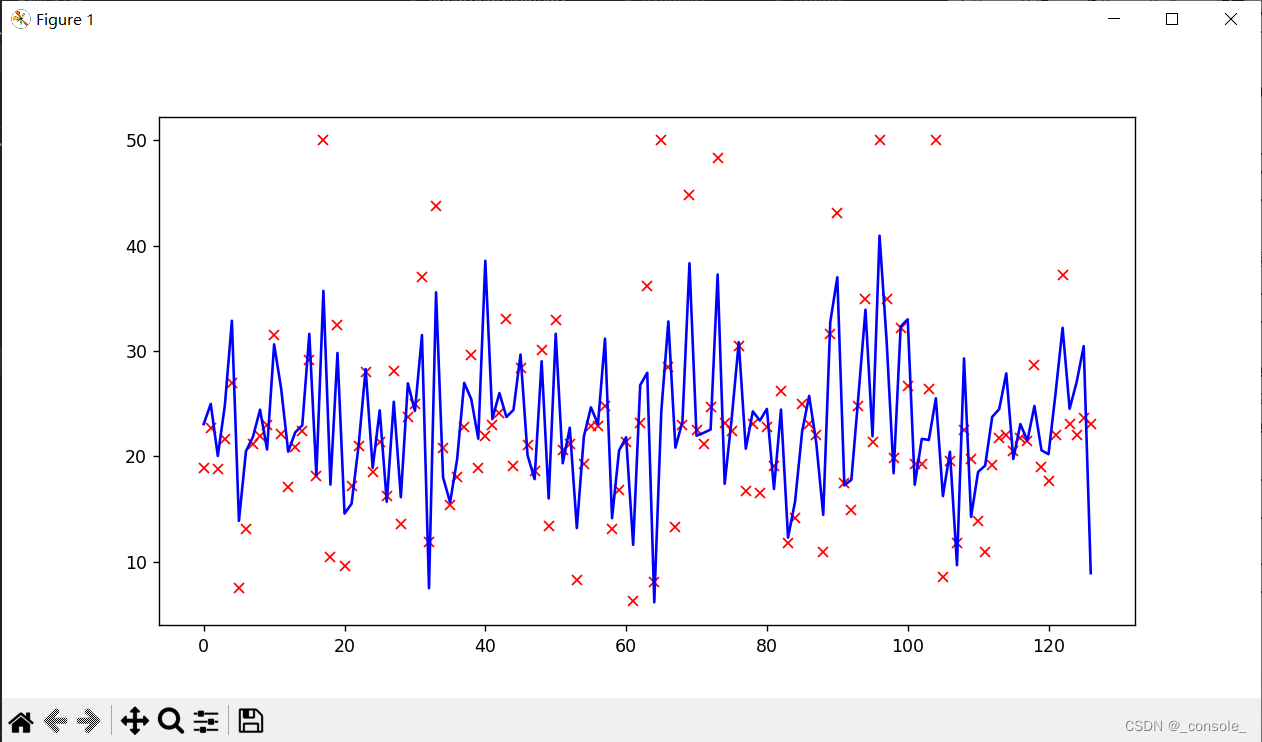
x = list(range(len(y_test)))
plt.plot(x,y_test,'rx')
plt.plot(x,y_predict,'b-')
plt.show()

回归模型评估

• 方法： 均方误差
• API sklearn.metrics.mean_squared_error

mse = mean_squared_error(y_test,y_predict)

岭回归

实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

• API

  • sklearn.linear_model.Ridge
  • 参数
    • alpha: 正则化力度，取值 0-1，1-10
    • solver：优化方法，默认auto
      • auto, svd, cholesky, lsqr, sparse_cg, sag, saga, lbfgs
    • normalize: 是否进行数据标准化

• 带有交叉验证的岭回归

  from sklearn.linear_model import RidgeCV
  

代码示例

波士顿房价预测

from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt 
import pandas as pd
import numpy as np

data = load_boston()

x_train,x_test,y_train,y_test = train_test_split(data.data,data.target,random_state=0)
transfer = StandardScaler()

#数据标准化
x_train=transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

reg = Ridge(max_iter=10000,alpha=0.8)
#使用LinearRegression
reg.fit(x_train,y_train)

print(reg.coef_,reg.intercept_)
y_predict = reg.predict(x_test)

# print(y_test)
# print(y_predict)
mse = mean_squared_error(y_test,y_predict)
print('方差为：',mse)

x = list(range(len(y_test)))
plt.plot(x,y_test,'rx')
plt.plot(x,y_predict,'b-')
plt.show()

逻辑回归

• 逻辑回归是分类算法，准确来说是解决二分类

• 激活函数

  • sigmoid函数

  $$g(x)=\frac{1}{1+e^{-x}}$$

  函数图像如下
  

• 输出结果

  • 大于0.5，输出1，小于0.5，输出0

• 损失函数

  • 对数似然损失
    $$cost(h_{\theta }(x),y)=\{\begin{array}{cc}-log(h_{\theta }(x))& ify=1\\ -log(1-h_{\theta }(x))& ify=0\end{array}$$
    函数图像

y=1时，预测结果（横轴）越接近1，损失越小

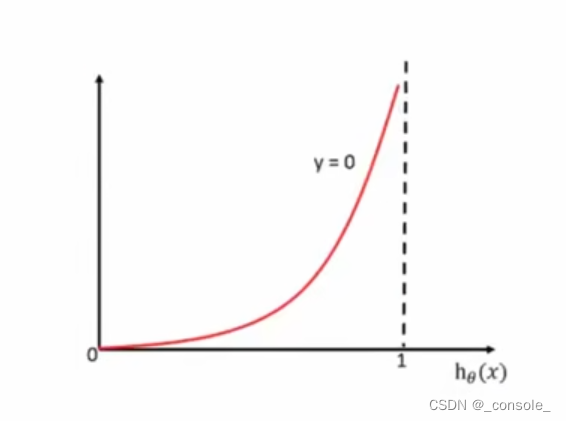
y=0时，预测结果（横轴）越接近1，损失越大

• 损失函数
  $$cost(h_{\theta }(x),y)=\sum _{i=1}^m(-y_{i}log(h_{\theta }(x))-(1-y_i)log(1-h_{\theta }(x)))$$