论文导读 | 关于内存子图匹配算法的调研

前言

近年来，图数据结构在学术界和工业界的应用越来越广泛，包括社交网络分析、道路分析、化学分子合成、生物蛋白质网络分析、金融欺诈检测等等。子图匹配（Subgraph Matching）是图分析领域研究的一个重要课题，其旨在一个大的数据图上匹配一个给定的查询子图，获得这个子图的所有同构嵌入（embedding）。由于子图匹配是一个NP-hard的问题，因此如何在一个大的数据图上有效的时间内枚举所有的查询结果是子图匹配问题研究的重中之重。当前对子图匹配问题的研究以提升查询效率为目的，本文主要调研了关于内存的子图匹配算法，对不同实现形式和不同实现框架的相关子图匹配工作进行了简要的介绍。

问题定义

给定一张数据顶点带标签的数据图 $G$ 、一个查询顶点带标签的查询图 $Q$ ，子图匹配问题是从数据图中找到所有的不同的子图，其中这些子图与查询图 $Q$ 是同构的，即对应顶点的标签要相同，对应顶点间的连边也要相同。

背景

子图匹配算法，在图分析领域有着广泛的应用，许多常见的图分析问题都可以被看作是子图匹配算法的延伸，子图匹配算法是它们重要的核心算子。例如，频繁图模式挖掘，旨在从一个大的数据图中挖掘出频繁的子图模式，多用于社区发现等算法；子图计数，旨在计算某一类子图在数据图中出现的次数，最常见也是最为人所广泛研究的就是三角形计数问题；子图搜索，旨在从许多数据图中找到包含某子图的那些数据图，也可以称为子图包含问题；图数据库中的图查询问题，如gStore的查询过程就可以看作是查询图在数据图中的匹配过程。由于子图匹配算法在图分析领域的广泛应用，研究如何加速子图匹配算法的性能就变得很有意义。一般而言，常见的子图匹配算法分为两种实现方式：基于探索的方法和基于连接的方法。基于探索的方法[2, 4, 5]采用的是Ullmann[1]提出的回溯模型，通过某一个查询顶点匹配顺序迭代地将查询顶点映射到数据顶点以扩展中间结果。换句话说，是按照匹配顺序进行深度优先搜索，如果下一个查询顶点没有有效的匹配或者到了最后的深度，那么就会递归回溯。基于连接的方法[3, 6]则不同，它们会将查询子图建模为一个关系查询，然后通过一系列的关系操作去执行这个查询，例如：选择操作（selection）和连接操作（join）。换句话说，它们是从关系（也就是边）的角度去匹配的。一些传统的关系数据库例如MonetDB和PostgreSQL会将子图匹配问题实现为一系列的二元连接，即每一步通过匹配一条边（关系）来扩展中间结果。一些最近的工作[3, 6]通过最坏情况下最优连接（WCOJ）的方式在每一步匹配连接到某一个查询顶点的多条边（关系）来扩展中间结果，获得了更好的性能。本文涉及的基于连接的方法采用的是WCOJ的连接方式。不管是用哪一种方式实现的子图匹配算法，都一般会采用下述两种框架之一：

直接枚举框架（direct-enumeration framework）：此类子图匹配算法不会提前产生辅助索引结构进行预处理，而是在枚举的过程中通过一些过滤策略对候选点进行剪枝，因此在枚举过程中是直接访问原数据图来匹配查询图的顶点和边的。
索引枚举框架（indexing-enumeration framework）：此类子图匹配算法会对数据图和给定的查询图进行预处理，生成辅助索引结构维护候选顶点和候选顶点之间的侯选边，在枚举过程中，匹配查询图的顶点和边时会访问这个索引结构而不是直接访问原来的数据图，这可以减少许多无效的访问。

下文将从两种不同的子图匹配框架的角度简述几个具有代表性的子图匹配算法，包括基于探索的方法和基于连接的方法。本文仅考虑内存中的串行精确算法。

直接枚举框架

QuickSI[2]是一篇比较经典的使用直接枚举框架的子图匹配算法，它是一种基于探索的方法。

对于一个给定的查询图，QuickSI提出了一种QI序列（QI-Sequence）的结构来约束在子图同构检验过程中的搜索空间大小。具体来说，一个查询图 $q$ 的QI序列可以被表示成如下的正则表达式： $SEQ_q = [[T_iR_{ij}^*]^\beta]$ 这个正则表达式可以被看成是 $q$ 的有根生成树的序列表示。其中，每个 $T_i$ 是生成树的一个节点，保存了该节点的基本信息，包括三个成员变量： $T_i.v$ 记录了查询顶点， $T_i.p$ 记录了该查询顶点在生成树中的父顶点， $T_i.l$ 记录了该查询顶点的标签。每一个 $T_i$ 后可能会跟着若干额外信息 $R_{ij}$ ，一种是度约束 $[d e g : d]$ ，保存查询顶点 $v_i$ 的度数，另一种是非树边 $[e d g e : k]$ ，记录与 $v_i$ 关联但没有出现在生成树中的边。注意，由于度数为2以下的点不会出现非树边，因此为避免冗余计算，不会记录度数为2以下的点的 $R_{ij}$ 信息。 $\beta$ 表示的是查询图中查询顶点的数目。很显然，每一个不同的图都会对应一个QI序列，因此子图匹配问题就被转化为了QI序列的匹配问题。QuickSI算法通过递归的方式迭代地匹配QI序列，如果数据图中的一个子图的QI序列可以完全匹配查询图的QI序列，那么就得到了一个结果。
每一个QI序列的顺序其实就对应了查询顶点的匹配顺序，而找到一个好的匹配顺序有利于加速子图同构检验的效率。QuickSI通过寻找最小生成树的方法来确定它的匹配顺序。具体来说，QuickSI首先将查询图 $q$ 转化为一个带权重的图 $q^w$ ，其中每个顶点 $u$ 的权重为 $\in V(G)|L(v)=L(u)}|$ ，每条边 $e(u,u^\prime)$ 的权重为 $w(e(u,u^\prime))=|{e(v,v^\prime) \in E(G)|L(v)=L(u) \wedge L(v^\prime)=L(u^\prime)}|$ ，然后根据边的权重找到最小生成树，最后从权重最小的边的权重最小的顶点开始得到一个有效的QI序列。

CBWJ[3]则是一篇使用直接枚举框架的基于连接的子图匹配算法，它的优化方向主要是生成有效的查询计划。

CBWJ使用动态规划的方法生成查询计划。CBWJ没有使用单一的二元连接或WCOJ，而是将二者结合，使用混合计划来优化子图匹配。CBWJ生成所有的计划空间（full plan space），每一个查询计划可以被表示为一棵查询树。其中，叶子节点被表示为查询图的一条查询边，CBWJ称其为SCAN操作，用于访问邻居列表匹配一条查询边。查询树的根节点表示原本的查询图。每个内部节点可能有一个子节点或两个子节点，如果只有一个子节点，那么相当于扩展了一个顶点，即采取了WCOJ的方式，将参与连接的多个顶点的邻居列表进行集合求交。如果有两个子节点，那么则是左右孩子进行二元连接得到的该节点，CBWJ使用Hash-join的方式执行二元连接操作。对于WCOJ计划，CBWJ引入了一个新的成本度量模型，称为交集代价（intersection cost，i-cost），它是由不同WCOJ计划访问和相交的邻接列表大小决定的。具体如下：
$\sum\limits_{Q_{k-1} \in Q_2...Q_{m-1}}^{} {\sum\limits_{t \in Q_{k-1}} {\sum\limits_{(i,dir) \in A_{k-1} s.t. (i,dir) is accessed}^{} {|t[i].dir|} } }$
其中， $A_{k-1}$ 是邻接列表描述符， $t$ 是一个部分匹配， $∣ t . d i r ∣$ 表示不同邻居列表的大小。对于二元连接计划，它的执行代价由它的两个孩子的产生的中间结果决定，假设它们分别有 $n_1$ 和 $n_2$ 个结果，那么代价为 $w_1 n_1+w_2 n_2$ ，其中 $w_1$ 是生成哈希表代价， $w_2$ 是哈希映射代价，这两个变量是由实验测量的。最后，CBWJ会用动态规划的方式枚举所有查询计划的代价，从中选择最优的查询计划。由于实际计算所有部分匹配的代价时不切实际的，因此WCOJ采用基数估计的方式估算查询计划的代价。很明显，查询计划空间的大小是与查询顶点数目呈指数相关的，因此当查询图变大时，生成查询计划的开销会很大，因此CBWJ对于大于10个顶点的查询只会每次枚举代价前5小的查询计划，此时查询计划可能只是局部最优。

由于查询计划是通过基数估计估算的查询代价，并且在整个枚举开始前提前生成的一个固定的全局计划，因此它有可能对于部分匹配来说不是一个好的查询计划。因此，CBWJ将包含两个或多个WCOJ操作的计划替换为了自适应的计划，它们可以通过实际的邻居列表大小修改全局的查询计划，以适应具体的环境。

索引枚举框架

CFL[4]是一篇比较经典的使用索引枚举框架的子图匹配算法，它是一种基于探索的方法。

CFL的一大贡献是提出了CFL分解的查询图分解方法，这个方法在其之后的很多子图匹配工作中都被使用。CFL分解的动机是希望延后笛卡尔积操作，而将具有更强剪枝能力的非树边验证尽可能的在回溯过程中提前处理。这样做可以减少无用的中间结果的产生。具体来说，CFL分解是core-forest-leaf分解的缩写，包括core-forest分解和forest-leaf分解。对于core-forest分解，一个core结构就是查询图的2-core（每个顶点的度数都大于等于2），而查询图的剩余部分则是一个forest结构。对于forest-leaf分解，将上一步forest中的所有一度顶点拿走作为leaf，剩下的就是forest结构。这样查询图就被分为了三个部分，CFL会按照core-forest-leaf的执行顺序分别进行匹配，因此非树边会被优先验证。
CFL提出了CPI辅助索引结构，它类似于一棵有着父子关系的BFS树，CPI中任意两个邻接顶点之间同样有着父子关系。CPI结构维护了每个查询顶点的候选点，并且维护了相邻顶点间的侯选边。如图所示：
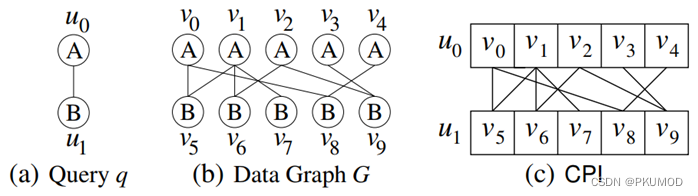
而对于匹配顺序的选择上，CFL利用CPI结构确定匹配顺序。对于一个core结构，其中查询顶点的匹配顺序是一个基于路径的顺序。由于CPI对应于一棵BFS树，因此一个core可以被分成多条根到叶子的路径，CFL通过贪心的方法依次选择代价最小的路径作为下一条路径。简单来说，CFL希望下一条路径生成的候选匹配越少越好，并且关联的非树边越多越好。对于forest来说也是同理，只不过没有了非树边的约束。

DAF[5]同样是一篇使用索引枚举框架的基于探索的子图匹配算法，它的性能在串行精确子图匹配算法中是比较优秀的。

由于CFL的CPI结构是以BFS生成树为基础的，因此它只能维护相邻顶点间的边，而对于非树边则没有维护，因此在枚举过程中，当匹配的查询顶点存在非树边时，CFL需要访问原数据图去验证非树边。DAF采用了有向无环图（DAG），用CS辅助索引结构减少候选空间。与CPI不同，CS不仅维护相邻顶点间的边，还维护不相邻顶点间的非树边，因此CS结构可以作为完整的搜索空间而不再需要原数据图。换句话说，CS结构是完备的。因此DAF只需要构造一个尽可能小的CS结构即可。DAF通过不断的交替使用查询 $Q$ 的有向无环图和反向无环图对CS结构进行自底向上的修剪，可以使CS结构不断缩小至收敛。当然，这样代价是很高的，因此DAF一般只会精简三次，此时大部分无效候选基本都被过滤了。
由于CFL的基于CPI的匹配顺序是一个全局的匹配顺序，因此对于许多部分匹配来说它是一个次优的匹配顺序。因此，DAF提出了一种可适应的匹配顺序。DAF的可适应的匹配顺序是以DAG顺序为基础的，对于一个部分匹配 $M$ 来说，查询 $Q$ 的有向无环图中的未访问的顶点 $u$ 的父顶点都已经在 $M$ 中被匹配了，那么 $u$ 就是可扩展的顶点，DAG顺序则是每一步要匹配的顶点都要从可扩展的顶点中选择。之所以称其为自适应的匹配顺序，由于每一步可扩展的顶点有很多，不同的部分匹配会根据不同的邻居列表分布计算得到不同的匹配顺序。每一个部分匹配都会选择产生局部候选最少的匹配顺序。
错误集修剪（pruning failing sets）。错误集定义了一些一定不会生成结果的扩展路径，而如果扩展路径上的点与错误集的点属于不同的祖先路径，那么这些部分结果都可以被剪枝。这个思想也被RapidMatch所采用。

RapidMatch[6]是一篇使用索引枚举框架的基于连接的子图匹配算法。

RapidMatch发现一般情况下，对于小查询图来说，基于连接的子图匹配算法性能较好，而对于大查询图来说，基于探索的子图匹配算法较好。通过对两种实现方式的算法的比较，RapidMatch认为基于探索的算法的性能优势很大程度上来自其辅助索引结构，而基于连接的算法之所以不利于大图，一方面正是由于它的直接枚举框架，它会访问更多的无效数据，另一方面是由于它产生的指数级的查询计划。因此，RapidMatch希望利用基于探索的方法中的优势来加快基于连接的子图匹配算法。
RapidMatch因此设计了个关系过滤器来减少关系的候选，其本质上是类似于基于探索的方法中预先生成辅助索引结构。它首先保存每个查询边的侯选边，然后根据查询顶点间的邻域关系对侯选边进行修剪，最后得到一个小且完备的候选空间。
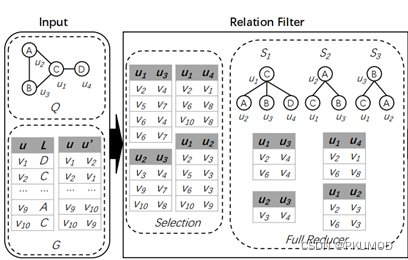
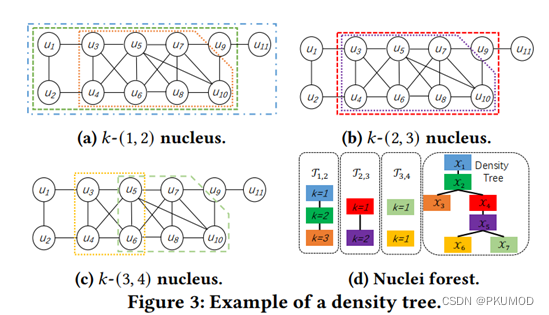
RapidMatch同样利用了CFL的查询图分解技术，不过它对core结构进行了进一步的分解，它利用了核分解（nucleus decomposition）的方法，将查询图的core结构分为了 $k - (1, 2)$ 核、 $k - (2, 3)$ 核、 $k - (3, 4)$ 核，其中 $k - (i, j)$ 表示图中每个顶点的度数大于等于 $i$ 且每条边的支持度大于等于 $j - 2$ 。如图所示，RapidMatch会将分解后的这些子图组织成密度树的形式，然后按照自底向上的执行顺序进行匹配。因此它的匹配顺序本质上可以看作是从查询图的连接密度高的部分开始匹配，因为一般来说这些子图是低频的。

在这里插入图片描述

总结

目前前沿的子图匹配相关工作大多都采用了索引枚举的框架，而且就大多数的实验结果来看，预先对查询图和数据图处理生成辅助索引结构的确可以有效的提高子图匹配的效率，不管是基于探索的方法还是基于连接的方法都倾向于采取这种方案。至于基于探索的方法和基于连接的方法的优劣，目前看来是各自有各自的优势。

参考文献

[1] Julian R Ullmann. 1976. An algorithm for subgraph isomorphism. Journal of the ACM (JACM) 23, 1 (1976), 31-42

[2] Haichuan Shang, Ying Zhang, Xuemin Lin, and Jeffrey Xu Yu. 2008. Taming verification hardness: an efficient algorithm for testing subgraph isomorphism. Proceedings of the VLDB Endowment 1, 1 (2008), 364-375.

[3] Amine Mhedhbi and Semih Salihoglu. 2019. Optimizing subgraph queries by combining binary and worst-case optimal joins. Proceedings of the VLDB Endowment 12, 11 (2019), 1692-1704.

[4] Fei Bi, Lijun Chang, Xuemin Lin, Lu Qin, and Wenjie Zhang. 2016. Efficient subgraph matching by postponing cartesian products. In Proceedings of the 2016 International Conference on Management of Data. 1199-1214.

[5] Myoungji Han, Hyunjoon Kim, Geonmo Gu, Kunsoo Park, and Wook-Shin Han. 2019. Efficient subgraph matching: Harmonizing dynamic programming, adaptive matching order, and failing set together. In Proceedings of the 2019 International Conference on Management of Data. 1429-1446.

[6] Shixuan Sun, Xibo Sun, Yulin Che, Qiong Luo, and Bingsheng He. 2020. Rapidmatch: a holistic approach to subgraph query processing. Proceedings of the VLDB Endowment 14, 2 (2020), 176-188.