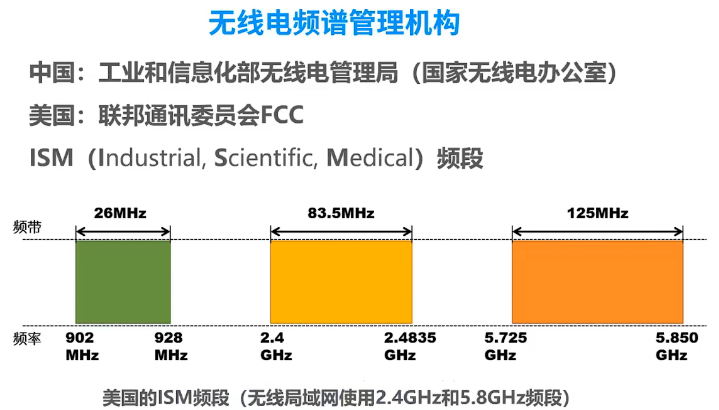
1. 利用邻接矩阵创建图并打印输出
2. 利用递归完成dfs算法遍历
3. 利用非递归完成bfs算法遍历
4. 利用prim算法得出最小生成树
5. 利用kruskal算法得出最小生成树

#include <iostream>

#include <cstdlib>//包含一些特定函数

#include <string>

//邻接矩阵结构存储图

#define what 0

#define maxvertex 10

#define maxedge 40

using namespace std;

typedef enum {DG,DN,UDG,UDN}graphkind;//以枚举存储图的种类

typedef char vertextype;//顶点数据类型

typedef struct arccell

{

int adj;//有权值则为权值

}adjmatrix[maxvertex][maxvertex];//创建一个能存储10个结点的邻接矩阵

typedef struct

{

vertextype vexs[maxvertex];//顶点向量

adjmatrix arcs;//邻接矩阵

int vexnum,arcnum;//图的当前顶点数和弧数

graphkind kind;

}mygraph;

mygraph G;

int visited[maxvertex];//创建一个标记数组

int locatevex(mygraph G,vertextype v1)

{

int i;

for(i=1;i<=G.vexnum;i++)//功能是找出顶点v1

{

if(G.vexs[i]==v1)

return i;

}

return -1;

}

int creatUDN(mygraph &G)

//创造一个无向图带权重

{

vertextype v1,v2;

int w,j,i;

cout<<"输入图的顶点数"<<endl;

cin>>G.vexnum;

cout<<"输入图的边数"<<endl;

cin>>G.arcnum;//记录顶点数和边数

cout<<"输入顶点向量(向量定义最小为1)"<<endl;

for(i=1;i<=G.vexnum;i++)

{

cin>>G.vexs[i];

}

for(i=1;i<=G.vexnum;i++)

for(j=1;j<=G.vexnum;j++)

{

G.arcs[i][j].adj=0;//权值进行初始化

}

for(int k=1;k<=G.arcnum;k++)//边的创建及边的权值的赋值

{

cout<<"输入边依附的两个顶点"<<endl;

cin>>v1>>v2;

cout<<"输入此边的权值"<<endl;

cin>>w;

i=locatevex(G,v1);

j=locatevex(G,v2);

G.arcs[i][j].adj=w;

G.arcs[j][i].adj=G.arcs[i][j].adj;//通过对i,j的位置分别赋值创建一个对称的邻接矩阵

}

return 1;

}

void dismygraph(mygraph G)

{

cout<<"图的邻接矩阵是："<<endl;

for(int i=1;i<=G.vexnum;i++)

{

for(int j=1;j<=G.vexnum;j++)//用for循环显示邻接矩阵

cout<<"  "<<G.arcs[i][j].adj;

cout<<endl;

}

}

void dfs(int V,int n)//n为顶点数

{

int w;

cout<<G.vexs[V]<<" ";

visited[V]=1;//当遍历过了就标记为1

w=1;

while(w<n && G.arcs[V][w].adj==0)//如果遍历还在顶点数范围内，并且邻接矩阵元素等于0，则跳过此元素继续遍历下去

w++;

while(w<=n)

{

if(visited[w]==0 && G.arcs[V][w].adj!=0)//如果标记数组未标记，并且邻接矩阵元素不等于0，则遍历此元素

dfs(w,n);

w++;

}

}

void bfs(int V,int n)//bfs遍历程序

{

int i,j,visit[10];

for(i=0;i<=n;i++)

visit[i]=0;//标记数组，并且初始化

cout<<G.vexs[1]<<" ";

visit[1]=1;

for(j=1;j<=n;j++)

for(i=1;i<=n;i++)

{

if(visit[i]==0 && G.arcs[j][i].adj!=0)//如果在同一行遇到不为0的就输出

{

visit[i]=1;//如果在下一行遇到同一个数不为0则无视

cout<<G.vexs[i]<<" ";

}

}

cout<<"  "<<endl;

}

void prim(int V,int n)

{

int lowcost[maxvertex][maxvertex],closest[maxvertex],a[maxvertex];

int i,j,k,m,min,b,g,sum;

sum=0;

for(m=1;m<=n;m++)

for(i=1;i<=n;i++)

{

lowcost[m][i]=G.arcs[m][i].adj;//将所有与第一个结点有关的结点的权值都记录下来

// closest[i]=1;//所有都标为未遍历，剩下第一个结点

}

lowcost[1][1]=0;//第一个结点标记为已遍历

k=1;

cout<<"1"<<"  "<<"0"<<endl;

for(i=1;i<n;i++)

{

a[i]=k;

min=maxedge;//将最大的权值赋给min

for(g=1;g<=i;g++)

{

b=a[g];

for(j=2;j<=n;j++)

{

if((lowcost[b][j]<min) && (lowcost[b][j]!=0) && G.vexs[j]!=0)//寻找最小的权值，并且权值不为0

{

min=lowcost[b][j];

k=j;

m=b;

}

}//经过循环后min有最小的权值，k为该结点

}

cout<<k<<"-"<<m<<"  "<<"权值为:"<<" "<<min<<endl;

sum=sum+min;

lowcost[b][k]=0;

G.vexs[k]=0;

}

cout<<"总权值为： "<<sum<<endl;

}

void kruskal(int V,int n)

{

int set[10], i, j,sum=0;//sum记录总权值

int k=1, a=1, b=1, min=maxedge;

for(i=1;i<=n;i++)

G.vexs[i]=i;//初始化顶点

for(i=1; i<=G.vexnum; i++)

set[i]=i;//各个顶点属于各个集合

while(k < G.vexnum)//有n-1条边将n个结点连在一起

{

for(i=1; i<=G.vexnum; i++)//对上半边矩阵进行遍历查找

for(j=i; j<=G.vexnum; j++)

if(G.arcs[i][j].adj<min && G.arcs[i][j].adj!=0)

{

min=G.arcs[i][j].adj;

a=i;

b=j;

}//找到最小的，并且没有被标记过的边记录下来

G.arcs[a][b].adj=0;//将找到的边标记为已读

if(set[a]!=set[b])//如果两个顶点不相同则打印，两个相等则形成了环路(边的两个顶点不属于一个集合)

{

printf("%d-%d  权值为: %d\n",G.vexs[a],G.vexs[b],min);

k++;//边数加1

sum=sum+min;

for(i=1; i<=G.vexnum; i++)

if(set[i]==set[b])//将顶点b所在集合并入顶点a集合

set[i]=set[a];

}

min=maxedge;//将标记当前最小边重置

}

cout<<"总权值为： "<<sum<<endl;

}

int main()

{//函数的调用和一些基本的打印提示语句

string input;

int i,n;

creatUDN(G);

dismygraph(G);

for(i=0;i<maxvertex;i++)//对标记数组进行初始化

visited[i]=0;

cout<<"深度遍历请输入A"<<endl;

cout<<"广度遍历请输入B"<<endl;

cout<<"prim算法生成最小生成树请输入C"<<endl;

cout<<"kruskal算法生成最小生成树请输入D"<<endl;

cout<<"end结束输入/输入错误重载输入"<<endl;

cin>>input;

while(input!="end")

{

if(input=="A")

{

cout<<"dfs遍历结果为："<<endl;

dfs(1,G.vexnum);

}

if(input=="B")

{

cout<<"bfs遍历结果为："<<endl;

bfs(1,G.vexnum);

}

if(input=="C")

{

cout<<"prim遍历结果为："<<endl;

prim(1,G.vexnum);

}

if(input=="D")

{

cout<<"kruskal遍历结果为："<<endl;

kruskal(1,G.vexnum);

}

cin>>input;

}

return 0;

}

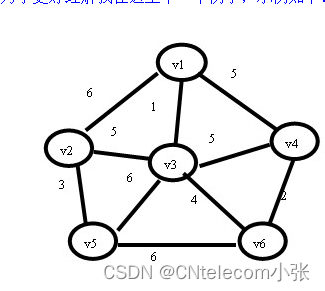
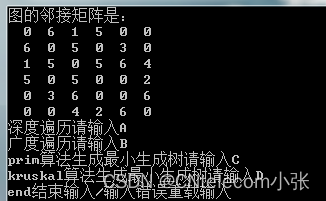
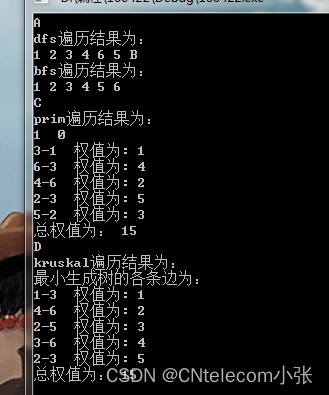
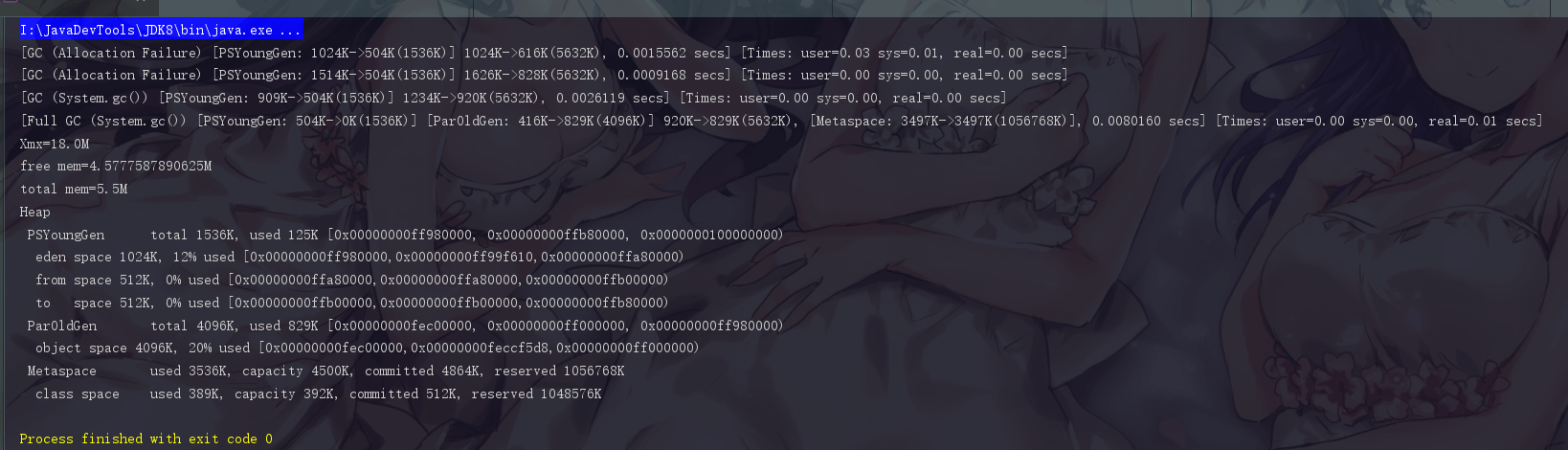
下面为程序运行截图：