一、本周周赛总结

• 只会T1\T3。
• T1对向双指针。
• T2 dp
• T3 dfs
• T4 贪心构造模拟

二、 [Easy] 2465. 不同的平均值数目

链接: 2465. 不同的平均值数目

1. 题目描述

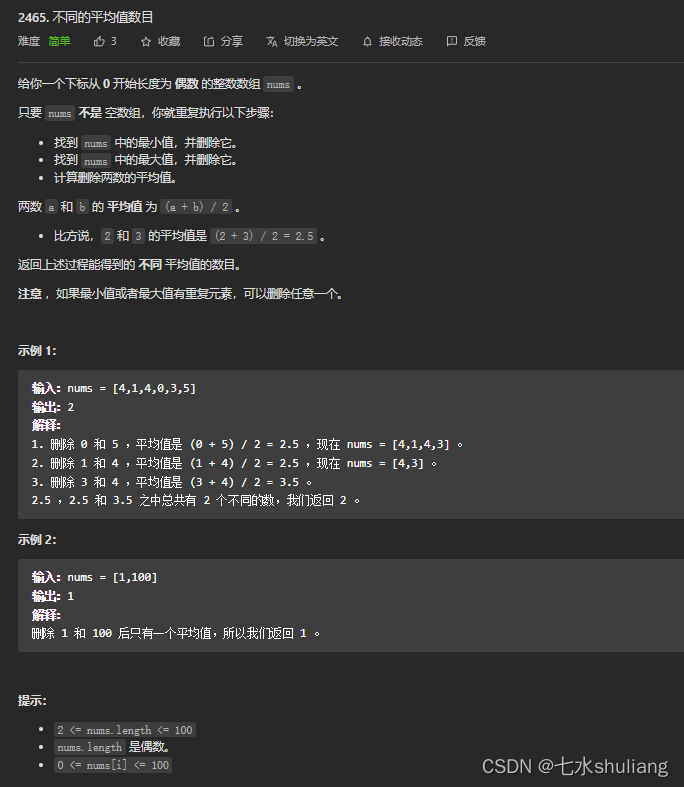
2. 思路分析

按题意模拟即可。

• 排序后使用对向双指针，避免下标算不明白。
• 注意由于平均值可能有浮点型为了避免精度损失直接记录和即可，相当于都乘2。

3. 代码实现

class Solution:
    def distinctAverages(self, nums: List[int]) -> int:
        nums.sort()
        n = len(nums)
        l, r = 0,n-1
        ans = set()
        while l < r:
            ans.add(nums[l]+nums[r])            
            l+=1
            r-=1
        return len(ans)

三、[Medium] 2466. 统计构造好字符串的方案数

链接: 2466. 统计构造好字符串的方案数

1. 题目描述

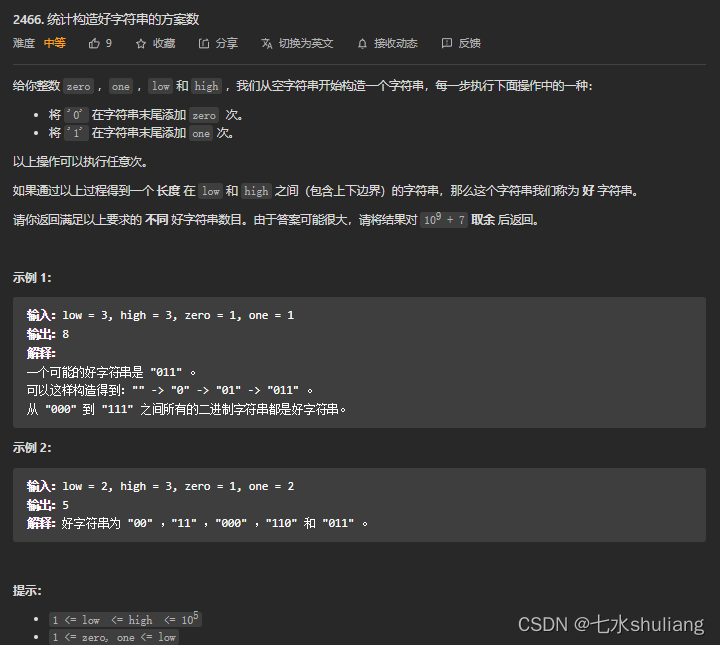
2. 思路分析

爬楼梯变装版。

• 真没想出来，后来说zero和one其实就是步数。
• 需要好好思索。

3. 代码实现

MOD = 10**9+7
class Solution:
    def countGoodStrings(self, low: int, high: int, zero: int, one: int) -> int:
        f = [0]*(high+1)
        f[0] = 1
        # f[zero] = 1
        # f[one] = 1
        for i in range(1,high+1):
            if i >= zero:
                f[i] += f[i-zero]
            if i >= one:
                f[i] += f[i-one]
            f[i] %= MOD
        return sum(f[low:]) % MOD

四、[Medium] 2467. 树上最大得分和路径

链接: 2467. 树上最大得分和路径

1. 题目描述

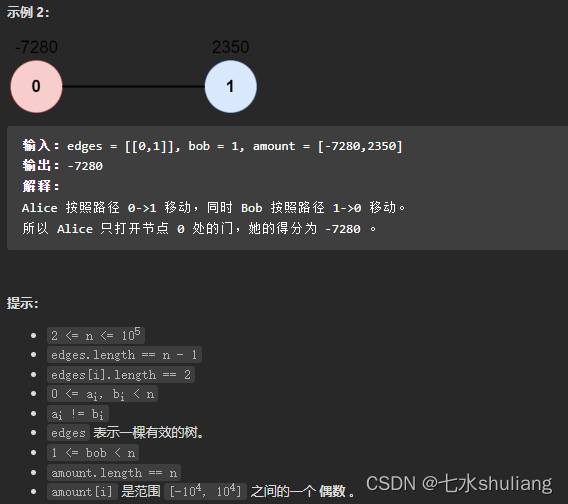
2. 思路分析

• 题目看似很长，其实题意比较简单，bob的路径和每个时刻的位置是固定的。因此可以先把bob的每个时刻位置求出来。
• 然后对alice的可能位置dfs，注意传入时间，来判断某个时刻bob是否到达了/已到达过这个位置，决定这个位置的得分是否能拿到。
• 因此两个dfs即可。
• 注意第二个dfs可以先根遍历也可以后根遍历，我个人觉得后根遍历好写；如果先根的话需要从根记录答案，向下传递。

3. 代码实现

class Solution:
    def mostProfitablePath(self, edges: List[List[int]], bob: int, amount: List[int]) -> int:
        n = len(edges)+1
        g = [[] for _ in range(n)]
        for u,v in edges:
            g[u].append(v)
            g[v].append(u)
        
        fas = {}
        def dfs(u,fa):
            fas[u] = fa
            for v in g[u]:
                if v != fa:
                    dfs(v,u)
        dfs(0,-1)
        
        b_path = {bob:0}
        t = 0
        b = 0
        while bob != -1:
            b_path[bob]=t
            t += 1
            b += amount[bob]
            # amount[bob] = 0
            bob = fas[bob]
        
        def f(u,fa,t):
            if fa!= -1 and len(g[u]) == 1:
                ans = 0
            else:                
                ans = -inf
            for v in g[u]:
                if v != fa:
                    ans = max(ans, f(v,u,t+1))
            print(u,ans,amount[u])
            if u not in b_path or t < b_path[u]:
                return ans + amount[u]
            if t == b_path[u]:
                return ans + amount[u]//2            
            return ans 
        return f(0,-1,0) 
        
        
            

五、[Hard] 2468. 根据限制分割消息

链接: 2468. 根据限制分割消息

1. 题目描述

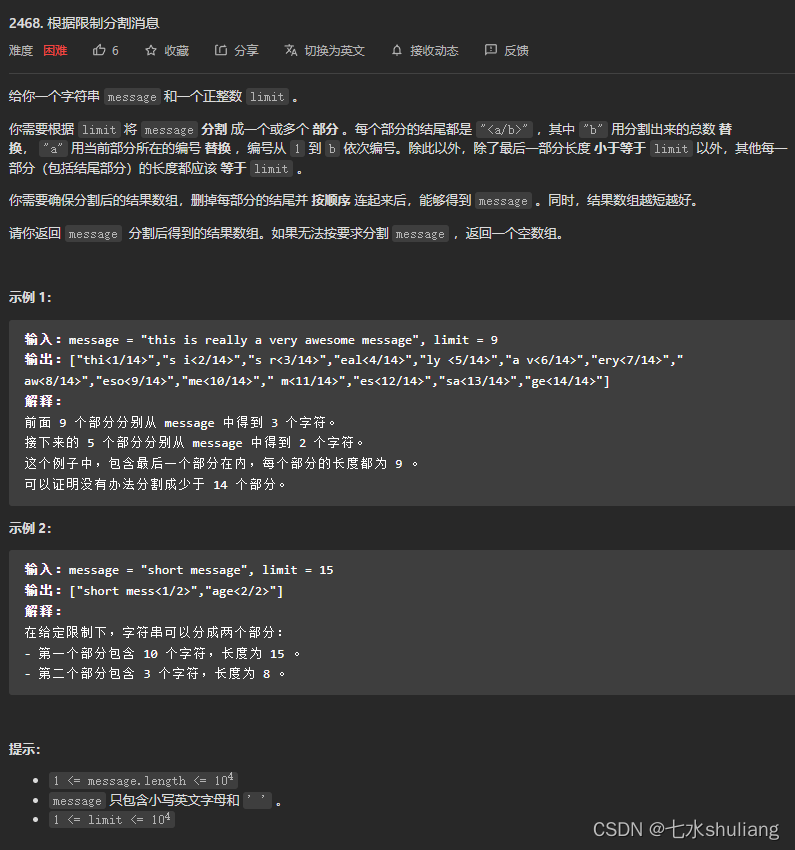
2. 思路分析

• 这题完全不会做，算构造模拟题吧。也可说是贪心枚举。
• 注意没有单调性，但分段是有单调性的，可能可以分段二分（在10,100，1000，10000的位置分段）。
• 显然message具体是啥没有用，只有长度n有用。
• 从小到大枚举分段数，计算在这个分段数下，能容纳多少个字符，容量cap需要>=n才表示可以构造答案了。
• 由于枚举是O(n),难点在于每次计算容量时是否能以O(1)或O(lg)的代价计算出cap，这里就是用了一些办法从上一个状态转移。
• 因此边转移边算就能算出来了。具体怎么算的可以看代码注释。

3. 代码实现

class Solution:
    def splitMessage(self, message: str, limit: int) -> List[str]:
        """贪心模拟，枚举分段数是i时，总共能容纳的字符长度，如果超过n，则可以产生答案；否则分段应该增加；如果发现结尾大于limit了，则无法构造
        要点在于如何线性的计算容量cap,即均摊O(1)的计算cap，这里是i增加时，从前一个i状态转移过来；而不是每次i增加都要从1枚举分段到i。
        时间复杂度，枚举i是O(n/(limit-tail_len)),构造答案是O(nlogn)
        """
        i = cap = 0
        n = len(message)
        while True:
            i += 1  # 枚举分段数，且枚举时认为这是最后一段，这样可以从前边状态转移(即计算了当分i段时，总共的i段加起来能容纳多少字母:cap)
            if i<10:
                tail_len = 5  # i<10时结尾形如<9/9>,长度是5
            elif i<100:  
                if i == 10:  # 如果分母多位了,前边的分母也要多位，从1位变2位，一共有9个
                    cap -= 9
                tail_len = 7  # i < 100时结尾形如<99/99>,长度是7
            elif i<1000:
                if i == 100:  # 如果分母多位了,前边的分母也要多位，从2位变3位，一共有99个
                    cap -= 99
                tail_len = 9
            else:
                if i == 100:
                    cap -= 999
                tail_len = 11
            if tail_len >= limit:
                return []
            cap += limit - tail_len
            if cap < n:
                continue
            ans = []
            k = 0
            for j in range(1,i):
                tail = f'<{j}/{i}>'
                m = limit - len(tail)
                ans.append(message[k:k+m]+tail)
                k += m
            
            ans.append(message[k:]+f'<{i}/{i}>')
            return ans

六、参考链接