前言

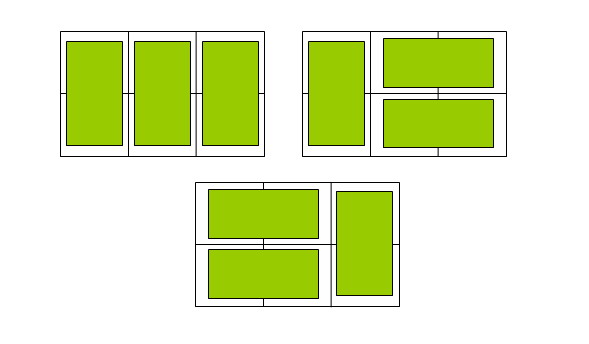
C40-1003-1.jpg (589×344) (hdu.edu.cn)

用1*2的骨牌铺满一个平面，是非常经典的一系列dp题目

(各大平台几乎都有这类题)

并且随着平面的要求不同，难度也是层层递增

对于n*m若数据量不同，则对应处理的算法也不一样

楼主本人还未完全理解明白这系列的所有题，因此本文主要就是为了记录代码，不做过多讲解

题目

2*n

awing:3687. 骨牌

51nod:骨牌覆盖 - 51Nod 1031

杭电：骨牌铺方格- 2046

若读者这题还不会，建议先学习学习基础的dp推导

/**
 * https://www.acwing.com/problem/content/3690/
 * 用 1×2 和 2×1 的骨牌铺满大小为 2×n 的地板，请问共有多少种不同铺法。
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int mod = 999983;
const int M = 10 + 10000;

int dp[M];

signed main() {
    int n;
    cin >> n;

    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i += 1) {
        // 竖着`1`，横着`二`
        dp[i] = dp[i - 1] + dp[i - 2];
        dp[i] %= mod;
    }

    cout << dp[n] << endl;

    return 0;
}

3*n

51nod:骨牌覆盖 V2 - 51Nod 1032

本题可以直接推到，也可以用状态机dp的思路

相关的思路的题目：专题：(经典dp) I型 L型铺盖2*n

推荐题解：XTU1161 骨牌（12的骨牌铺N3的地板）

/**
 * https://vjudge.csgrandeur.cn/problem/51Nod-1032
 * 骨牌覆盖 V2
 * 3 * n 放 1*2的骨牌，求摆放种类
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int mod = 1e9 + 7;
const int M = 10 + 1000;

// 定义考虑作用第i列的时候
// 第i列所处状态的方案数
int dp[M][2 * 2 * 2];

signed main() {
    int n;
    cin >> n;

    // 或者从0开始初始化
    // 0状态，铺满当作墙壁
    dp[0][0b111] = 1;
    // dp[1][0b000] = 1;
    // dp[1][0b011] = 1;
    // dp[1][0b110] = 1;
    // 110和011对称
    // 100和001对称
    // 010和101是无限循环永远为0的情况
    for (int i = 1; i <= n; i += 1) {
        dp[i][0b111] = (dp[i - 1][0b011] + dp[i - 1][0b110] + dp[i - 1][0b000]) % mod;
        // 这为什么不 2 * dp[i - 1][0b001]
        // 因为我们定义的是作用于第i列
        // 若先构成了dp[i-1][0b111]再转换则违背定义
        // 且会和单独考虑dp[i-1][0b111]冲突，或者说就是包含在这里了
        dp[i][0b110] = (dp[i - 1][0b111] + dp[i - 1][0b001]) % mod;
        dp[i][0b101] = (dp[i - 1][0b010]) % mod;
        dp[i][0b100] = (dp[i - 1][0b011]) % mod;
        dp[i][0b011] = (dp[i - 1][0b111] + dp[i - 1][0b100]) % mod;
        dp[i][0b010] = (dp[i - 1][0b101]) % mod;
        dp[i][0b001] = (dp[i - 1][0b110]) % mod;
        dp[i][0b000] = (dp[i - 1][0b111]) % mod;
    }

    cout << dp[n][0b111] << endl;
    return 0;
}

交流群的一位大佬直接用代码写代码

        dp[i][0b111] = (dp[i][0b111] + dp[i - 1][0b000]) % mod;
        dp[i][0b110] = (dp[i][0b110] + dp[i - 1][0b001]) % mod;
        dp[i][0b101] = (dp[i][0b101] + dp[i - 1][0b010]) % mod;
        dp[i][0b100] = (dp[i][0b100] + dp[i - 1][0b011]) % mod;
        dp[i][0b111] = (dp[i][0b111] + dp[i - 1][0b011]) % mod;
        dp[i][0b011] = (dp[i][0b011] + dp[i - 1][0b100]) % mod;
        dp[i][0b010] = (dp[i][0b010] + dp[i - 1][0b101]) % mod;
        dp[i][0b001] = (dp[i][0b001] + dp[i - 1][0b110]) % mod;
        dp[i][0b111] = (dp[i][0b111] + dp[i - 1][0b110]) % mod;
        dp[i][0b000] = (dp[i][0b000] + dp[i - 1][0b111]) % mod;
        dp[i][0b011] = (dp[i][0b011] + dp[i - 1][0b111]) % mod;
        dp[i][0b110] = (dp[i][0b110] + dp[i - 1][0b111]) % mod;

///    

	private static String not(String state) {
		char[] data = state.toCharArray();
		for (int i = 0; i < data.length; i++) {
			data[i] = data[i] == '1' ? '0' : '1';
		}
		return String.valueOf(data);
	}
	
	private static boolean canConvertTo(String state1, String state2) {
		state1 = not(state1);
		if (state1.equals(state2)) return true;
		if (state1.startsWith("00")) {
			if (("11" + state1.charAt(2)).equals(state2)) {
				return true;
			}
		}
		if (state1.endsWith("00")) {
			if ((state1.charAt(0) + "11").equals(state2)) {
				return true;
			}
		}
		return false;
	}

n*m

n < 5 && m < 1e9

51nod:骨牌覆盖 V2 - 51Nod 1033

计算出第一行的所有情况

在叠加行数，用矩阵快速幂叠加

/**
 * https://vjudge.csgrandeur.cn/problem/51Nod-1033
 * 2个数M N，中间用空格分隔（2 <= m <= 10^9，2 <= n <= 5）
 * ==============================================
 * 参考题解：
 * https://blog.csdn.net/blessLZH0108/article/details/78106856
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int mod = 1e9 + 7;
// n <= 5
int n, m;

// 矩阵乘法
vector<vector<int>> matrixMultiply(const vector<vector<int>>& matrixA,
                                   const vector<vector<int>>& matrixB) {
    int n = matrixA.size();
    int m = matrixA[0].size();
    int p = matrixB[0].size();
    vector<vector<int>> ans(n, vector<int>(p));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            for (int k = 0; k < p; k++) {
                ans[i][k] = (ans[i][k] + matrixA[i][j] * matrixB[j][k]) % mod;
            }
        }
    }
    return ans;
}
// 快速幂，此处不考虑0次幂的情况
vector<vector<int>> matrixBinPow(vector<vector<int>> matrix, int k) {
    if (k == 1) {
        return matrix;
    }
    // 迭代法，单位矩阵
    // vector<vector<int>> ans(matrix.size(), vector<int>(matrix[0].size()));
    // for (int i = 0; i < ans.size(); i += 1) {
    //     ans[i][i] = 1;
    // }
    // while (k) {
    //     if (k & 1) {
    //         ans = matrixMultiply(ans, matrix);
    //     }
    //     matrix = matrixMultiply(matrix, matrix);
    //     k >>= 1;
    // }
    // return ans;

    auto ans = matrixBinPow(matrix, k >> 1);
    ans = matrixMultiply(ans, ans);
    if (k & 1) {
        return matrixMultiply(ans, matrix);
    } else {
        return ans;
    }
}

void dfs(vector<vector<int>>& matrix, int col, int pre, int cur) {
    // dp[pre][cur]=1，表示能从pre状态转换到cur状态
    if (col == n) {
        matrix[pre][cur] = 1;
        return;
    }
    //竖放，第col+1列由空变为放骨牌
    dfs(matrix, col + 1, pre << 1, cur << 1 | 1);
    //不放，第col+1列由放骨牌变为空
    dfs(matrix, col + 1, pre << 1 | 1, cur << 1);
    //横放，col+1和col+2列均放骨牌
    if (col + 2 <= n) {
        dfs(matrix, col + 2, pre << 2 | 3, cur << 2 | 3);
    }
}

signed main() {
    cin >> m >> n;
    int mask = 1 << n;
    m += 1;
    
    // 定义dp[][] 位于ij的种类数
    vector<vector<int>> matrix(mask, vector<int>(mask));
    dfs(matrix, 0, 0, 0);

    matrix = matrixBinPow(matrix, m);
    cout << matrix[0][mask - 1] << endl;

    return 0;
}

n*m < 100

杭电:Mondriaan’s Dream- 1400

poj:2411 – Mondriaan’s Dream

52nod:骨牌覆盖 V3 - 51Nod 1034 一直Runtime Error似乎是个历史遗留问题

2411_1.jpg (599×33) (poj.org)

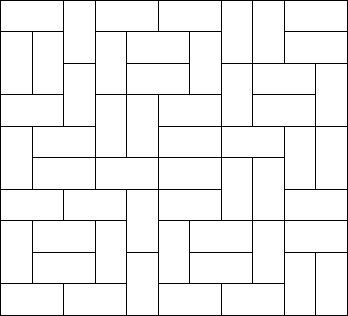
2411_2.jpg (348×316) (poj.org)

n*m < 100 -> min(n, m) <= 10

一行一行处理，每个点三种可能

与上一层竖放
与前一个横放
不放

/**
 * https://vjudge.csgrandeur.cn/problem/POJ-2411
 * Mondriaan's Dream
 * 1*2的骨牌摆放n*m
 */
#include <string.h>

#include <iostream>
using namespace std;
#define int long long

// 滚动数组
// 第一位滚动，便于初始化
int dp[2][1 << 12];

signed solve(int n, int m) {
    memset(dp, 0, sizeof(dp));
    // 让m作为较小的一个
    if (n < m) {
        swap(n, m);
    }
    int MASK = 1 << m;

    // 假设处理前的一个状态是满状态的
    dp[0][MASK - 1] = 1;
    int cur = 0;
    // 处理行数
    for (int row = 0; row < n; row += 1) {
        // 处理列，列<行
        for (int col = 0; col < m; col += 1) {
            // 混动数组
            cur ^= 1;
            int pre = cur ^ 1;
            memset(dp[cur], 0, sizeof(dp[cur]));
            for (int mask = 0; mask < MASK; mask += 1) {
                // 前一轮的状态为空，则无法转移
                if (dp[pre][mask] == 0) {
                    continue;
                }

                // 不放，mask<<1让 mask 的最后一位为0
                int change = mask << 1;
                if (change & (1 << m)) {
                    dp[cur][change ^ (1 << m)] += dp[pre][mask];
                }

                // 竖着放，不是第一行，而且上面的位置没放
                if (row && !(mask & (1 << (m - 1)))) {
                    change = (mask << 1) ^ (1 << m) ^ 1;
                    dp[cur][change ^ (1 << m)] += dp[pre][mask];
                }

                // 横着放，不是第一列，且左侧为空
                if (col && !(mask & 1)) {
                    change = (mask << 1) ^ 3;
                    dp[cur][change ^ (1 << m)] += dp[pre][mask];
                }
            }
        }
    }

    cout << dp[cur][MASK - 1] << endl;

    return 0;
}

signed main() {
    int n, m;
    while (cin >> n >> m) {
        if (n == 0 && m == 0) {
            break;
        }
        solve(n, m);
    }

    return 0;
}