【HDU No. 1232】 畅通工程

杭电OJ 题目地址

【题意】

现有城镇道路统计表，表中列出了每条直接相连的城镇道路。“畅通工程”的目标是使全省任意两个城镇间都可以通过道路连接（间接通过路连接也可以）。问最少还需要建设多少条道路？

【输入输出】

输入：

输入包含多个测试用例，每个测试用例的第1行都包含两个正整数，分别是城镇数量N （N <1000）和道路数量M ；随后的M 行对应M 条道路，每行都给出一对正整数，分别是该条道路连接的两个城镇的编号。城镇编号为1～N 。

注意：两个城市之间可以有多条道路相通。当N 为0时，输入结束。

输出：

对每个测试用例，都单行输出最少还需要建设的道路数量。

【样例】

【思路分析】

可以将一个连通分量看作一个集合，一条道路可以使两个连通分量通起来，相当于两个集合的合并。

因此只要统计道路网络的连通分量数ans，再添加ans-1条道路即可。使用并查集可轻松解决。

【算法设计】

① 初始化。初始化每个节点的集合号为其自身。

② 合并。每输入一条边的两个端点x 、y ，都合并x、y 的集合。

③ 统计并输出结果。统计有多少个集合（集合号等于自身），每个集合都相当于一个连通分量，若有ans个集合，则添加ans- 1条边即可使其连通。最少还需要建设ans-1条道路。

【完美图解】

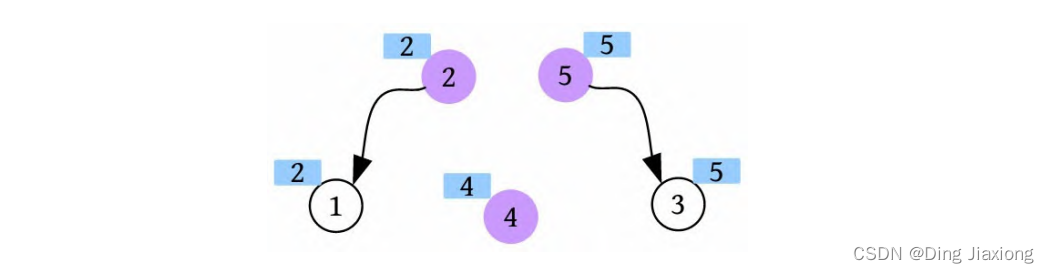
5个城镇，两条道路（1-2、3-5），一共3个集合，只需修建两条道路即可。

【算法实现】

#include<cstdio>

using namespace std;

#define N 1010

int fa[N];

int Find(int x){
	
	if(x != fa[x]){
		
		fa[x] = Find(fa[x]);
	}
	return fa[x];
}

void Union(int x , int y){
	
	int a = Find(x);
	int b = Find(y);
	
	if(a != b){
		fa[a] = b;
	}
}

int main(){
	
	while(1){
		
		int n , m , i , ans = 0 , x , y;
		scanf("%d" , &n);
		if(n == 0){
			
			break;
		}
		scanf("%d" , &m);
		for(int i = 1; i <= n ; i++){
			
			fa[i] = i;
		}
		for(int i = 0 ; i < m ; i ++){
			
			scanf("%d%d" , &x , &y);
			Union(x , y);
		}
		for(int i = 1 ; i <= n ; i ++){	
				
			if(i == fa[i]){
				
				ans ++;
			}
		}
		printf("%d\n" , ans - 1);
	}
	return 0;
}