C++数据结构X篇_18_二叉树的创建（根据遍历结果创建二叉树；#号法创建树）

news2024/10/6 0:33:12

本篇将会介绍二叉树的创建，重点学习#号法创建树的方法。

文章目录

1. 根据遍历结果创建二叉树（只需记住结论即可）
- 1.1 首先有一个问题，根据中序遍历的结果能确定一棵树吗？
- 1.2 那如何才能确定一棵树？（带中序的可以确定一个树）
- 1.3 举例
2. #号法创建树（重点）
- 2.1 什么是#号法创建树？
- 2.2 #号法创建树的代码实现

1. 根据遍历结果创建二叉树（只需记住结论即可）

1.1 首先有一个问题，根据中序遍历的结果能确定一棵树吗？

举例：中序遍历结果为：“12345”，这个“12345”能确定一棵树吗？

请思考，会有多少种形状，树的形状能唯一确定吗？
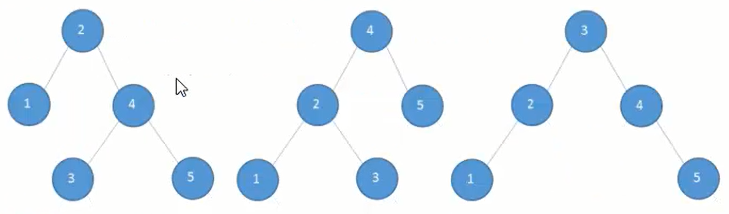
在这里插入图片描述
从上面的结果可以看出，根据某一个遍历结果显然是无法确定树的形状的，这是因为你无法确认是左子树还是右子树。

1.2 那如何才能确定一棵树？（带中序的可以确定一个树）

结论：

通过中序遍历和先序遍历可以确定一个树
通过中序遍历和后续遍历可以确定一个树
通过先序遍历和后序遍历确定不了一个树

1.3 举例

假设有两组结果：
先序遍历结果：A D E B C F
中序遍历结果：D E A C F B
根据先序遍历结果知道二叉树的根节点为A，从中序遍历结果知道二叉树的左子树为：DE，右子树为：CFB
结合分析先序和中序遍历结果，得到如下二叉树：
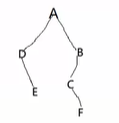
在这里插入图片描述

2. #号法创建树（重点）

2.1 什么是#号法创建树？

创建树，让树的每一个节点都变成度数为 2的树

先序遍历结果：124###3## （#代表null即空）
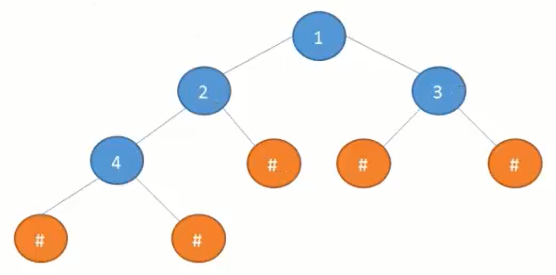
在这里插入图片描述

2.2 #号法创建树的代码实现

#include <iostream>
using namespace std;


//定义二叉树节点
class binarynode
{
public:
	char ch;			 //节点数据域
	binarynode* lchild;  //左孩子
	binarynode* rchild;  //右孩子
};

void recursion(binarynode* root)
{
	if (root == nullptr)
	{
		return;
	}
	cout << root->ch;
	recursion(root->lchild);
	recursion(root->rchild);
}

//创建树
binarynode* createBinaryTree()
{
	//清空输入缓存区
	fflush(stdin);

	//等待输入
	char ch;
	scanf("%c", &ch);

	binarynode* node;
	binarynode* lchild;  //左孩子
	binarynode* rchild;  //右孩子

	if (ch == '#')
	{
		node = nullptr;
	}
	else
	{
		lchild = createBinaryTree();
		rchild = createBinaryTree();	

		node = new binarynode;
		node->ch = ch;
		node->lchild = lchild;
		node->rchild = rchild;
	}

	return node;
}

int main()
{
	//创建树
	binarynode* root=createBinaryTree();
	//打印树
	recursion(root);
	system("pause");
	return 0;
}