题目：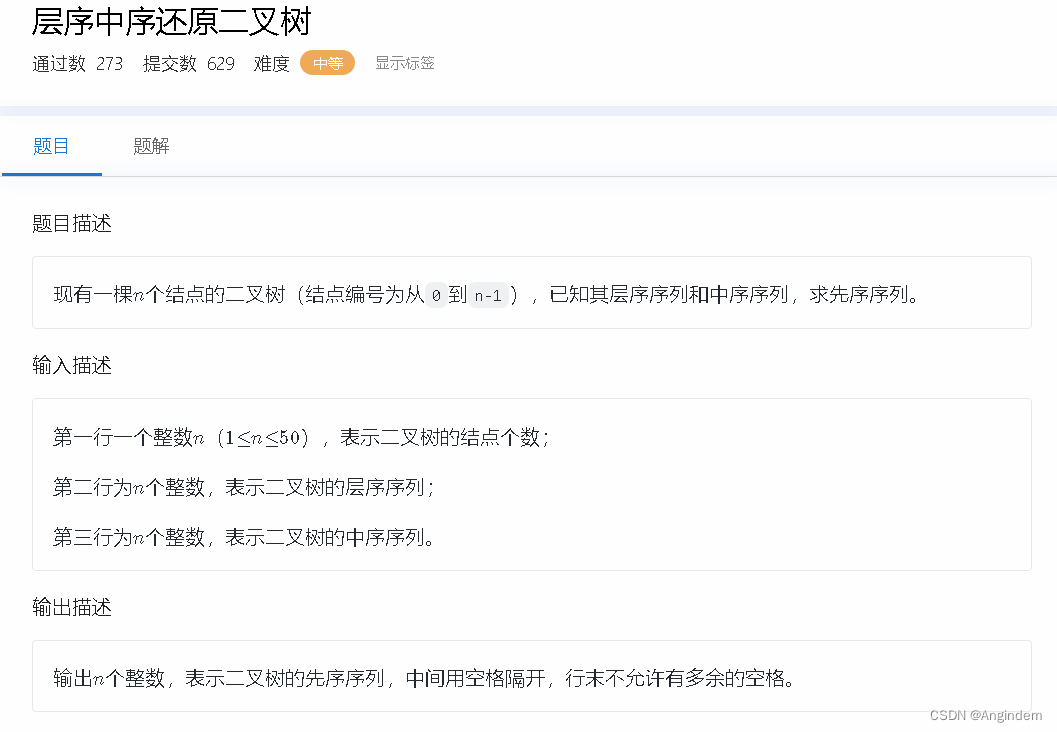

样例：

6
0 2 5 1 4 3
1 2 4 0 5 3

思路：

        这道题，核心思想就是  结合 层序遍历的性质，根据 中序来判断左右孩子是否存在。

前中后序的遍历实现，主要都是 递归的形式实现遍历

而层序遍历是  按照 BFS 的形式迭代遍历 ，以一层一层的搜的。

所以我们建树的时候结合 BFS 的层序规则建树

层序遍历数组中，第一个元素一定是根节点，随后不断的结合 中序数组判断左右子树

代码详解如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;

// 定义结点结构体
struct Node
{
	int val;
	Node*lchild;
	Node*rchild;
	
	// 定义构造函数
	inline Node():val(-1),lchild(NULL),rchild(NULL){};
	// 定义有参构造函数
	inline Node(int x):val(x),lchild(NULL),rchild(NULL){};
}*q[N];		// q 为存储二叉树结点

int n;	// 二叉树结点个数

umap<int,int>inorder,lorder;	// 定义中序数组和层序数组

umap<int,bool>st;	// 标记当且结点是否已经确定过了

// 中序层序建树函数
inline void biuldTree()
{
	// i 为 当且结点，j 为当前下一个结点
	for(int i = 0,j = 1;j < n;)
	{
		// 这一层是层序遍历的效果
		for(int end = j;i < n;++i)
		{
			// 这一层是遍历当前层数的结点个数
			
			int p = inorder[lorder[i]];	// 获取当且结点在中序数组中的下标
		
			st[p] = true;	// 确定当前中序数组下标
			
			if(p && !st[p - 1])
			{
				// 如果左孩子存在，那么给当前结点建树左孩子
				q[i]->lchild = new Node(lorder[j]);
				
				// 这里 j++ = q[i].lchild 是给下一层结点遍历使用
				q[j++] = q[i]->lchild;
			}
			
			if(p + 1 < n && !st[p + 1])
			{
				// 如果右孩子存在，那么给当前结点建树右孩子
				q[i]->rchild = new Node(lorder[j]);
				
				// 这里 j++ = q[i].lchild 是给下一层结点遍历使用
				q[j++] = q[i]->rchild;
			}
		}
	}
}

// 前序遍历函数
void preorder(Node* root)
{
	if(root == NULL) return ;
	cout << root->val;
	if(--n) cout << ' ';
	preorder(root->lchild);
	preorder(root->rchild);
}

inline void solve()
{
	cin >> n;
	// 输入层序遍历数组
	for(int i = 0;i < n;++i)
	{
		cin >> lorder[i];
	}
	// 记录中序遍历数组的下标
	for(int i = 0,x;i < n;++i)
	{
		cin >> x;
		inorder[x] = i;
	}
	
	q[0] = new Node(lorder[0]);	// 确定根节点
	
	biuldTree();	// 开始建树
	
	preorder(q[0]);	// 前序遍历
}

int main()
{
//	freopen("a.txt", "r", stdin);
	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：