认识信道(零):天线的极化
文章目录
- 认识信道(零):天线的极化
- 零.简述
- 一.平面电磁波的传播
- 二.对于field pattern的研究
- 三.对于传播路程的研究
- 四.极化失配
- 五.传播结果
- 六.QuaDRiGa Tutorial分析
- TXV-RXV
- TX45-RXV和 TXV-RX45
- TX45-RX45
- TX90-RX0,45,90
零.简述
本人本科没有学过电磁波课程,这里用的都是最浅显的道理来解释电磁波的极化,试图让理论自洽,如有错误,烦请指正。
一.平面电磁波的传播
首先我们这里描述的极化,是天线在远场的极化,它是一种平面波的极化,我们知道,平面波的传播方向为
S
=
E
×
H
S = E \times H
S=E×H
他垂直于电场和磁场
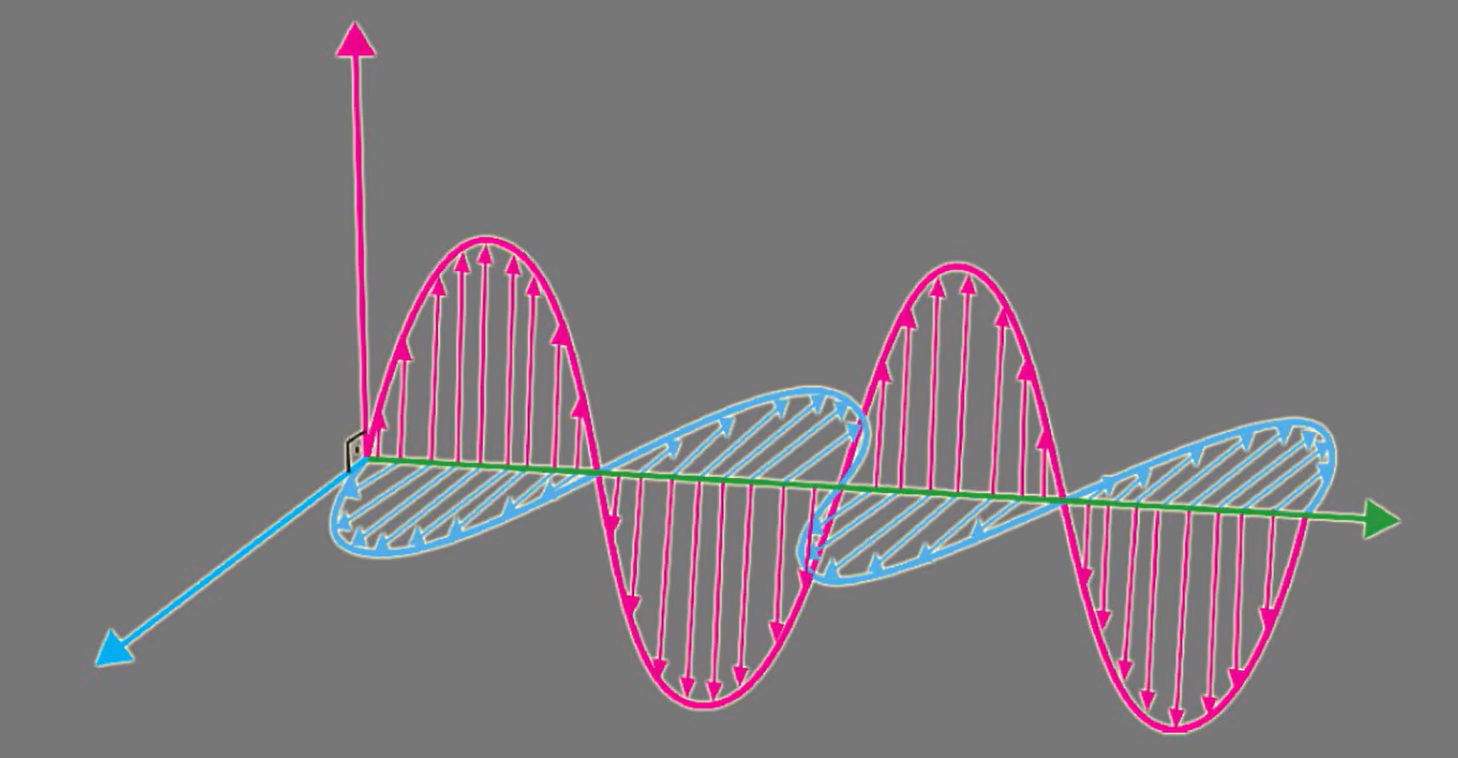
因此我们可以得到,当一个电磁波沿z轴传播,他在z轴上并没有分量,而可以在x,y轴上正交
由此可以得到以下推导

也就是说,我们会研究垂直于传播方向平面上的一组正交基对于幅度和相位的分解,这就是天线极化研究的核心问题
当我们把他扩展到球坐标系下,对于电磁波的传播方向r,天然的存在一组垂直于传播方向的正交基,也就是 θ \theta θ和 ϕ \phi ϕ
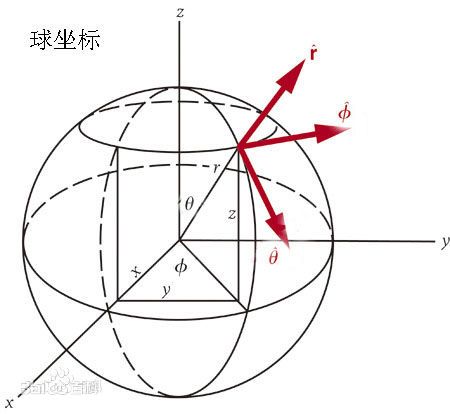
因此,我们常常将电场分解到 θ \theta θ和 ϕ \phi ϕ方位上来研究
二.对于field pattern的研究
对于field pattern的研究,其实也就是对于幅度的研究,因为他确定了我们的power大小
对于一个确定的传播方向,那么他的Field Pattern自然也就有两个分量
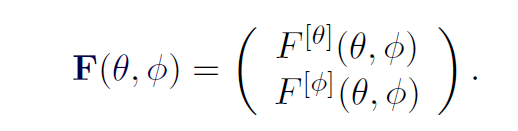
这里以一个半波偶极子天线举例
他正常两个分量为
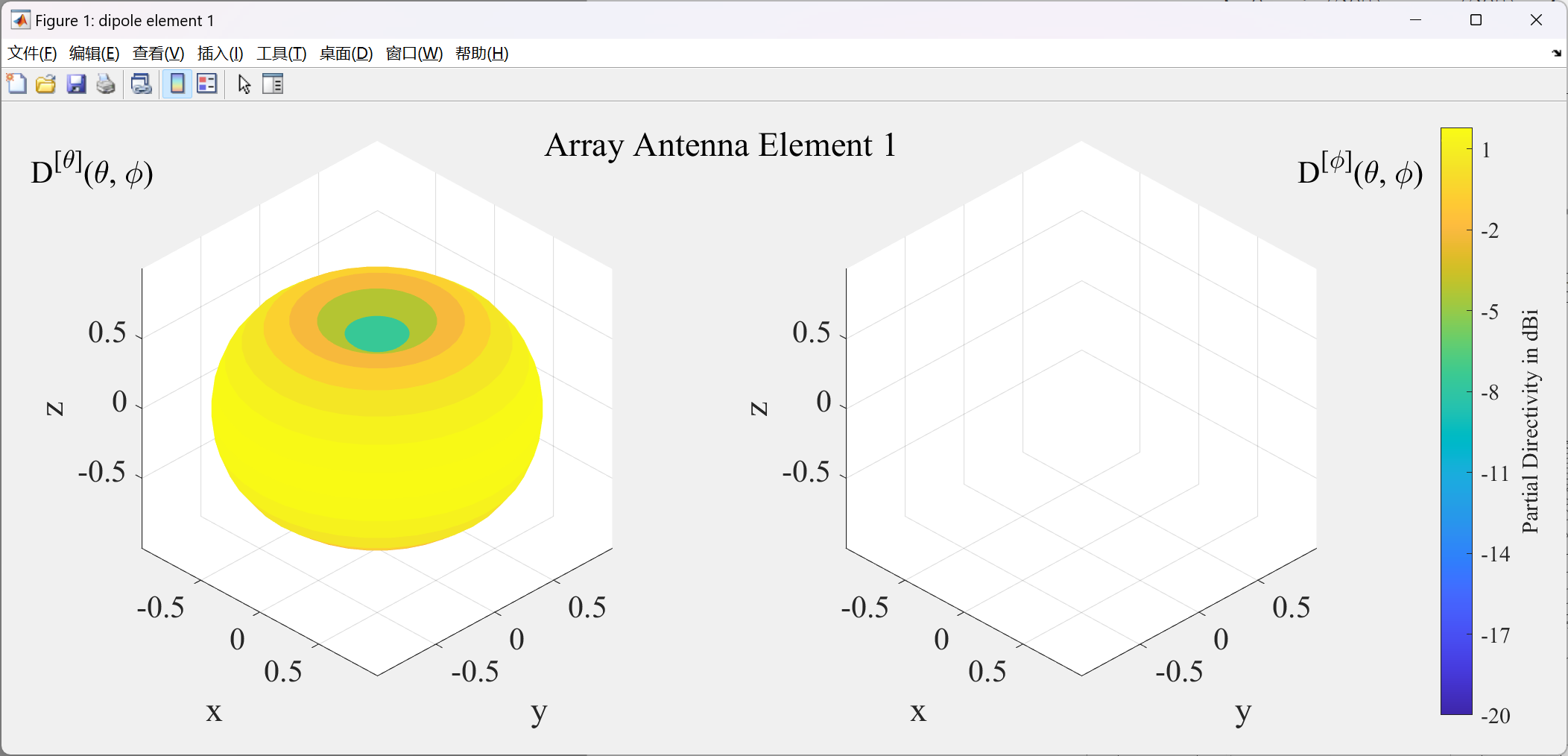
即只有 θ \theta θ方向上的分量,这也是符合直觉的,因为 θ \theta θ方向上是E的方向, ϕ \phi ϕ方向上是磁场的方向
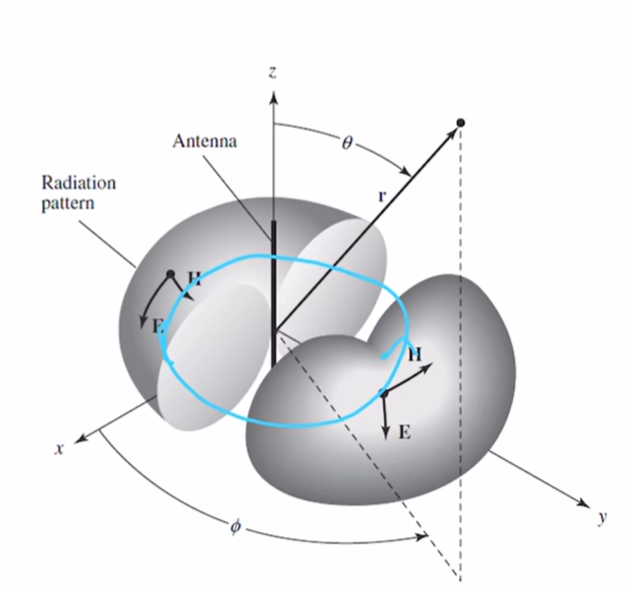
绕x旋转45°的半波偶极子的场方向图为
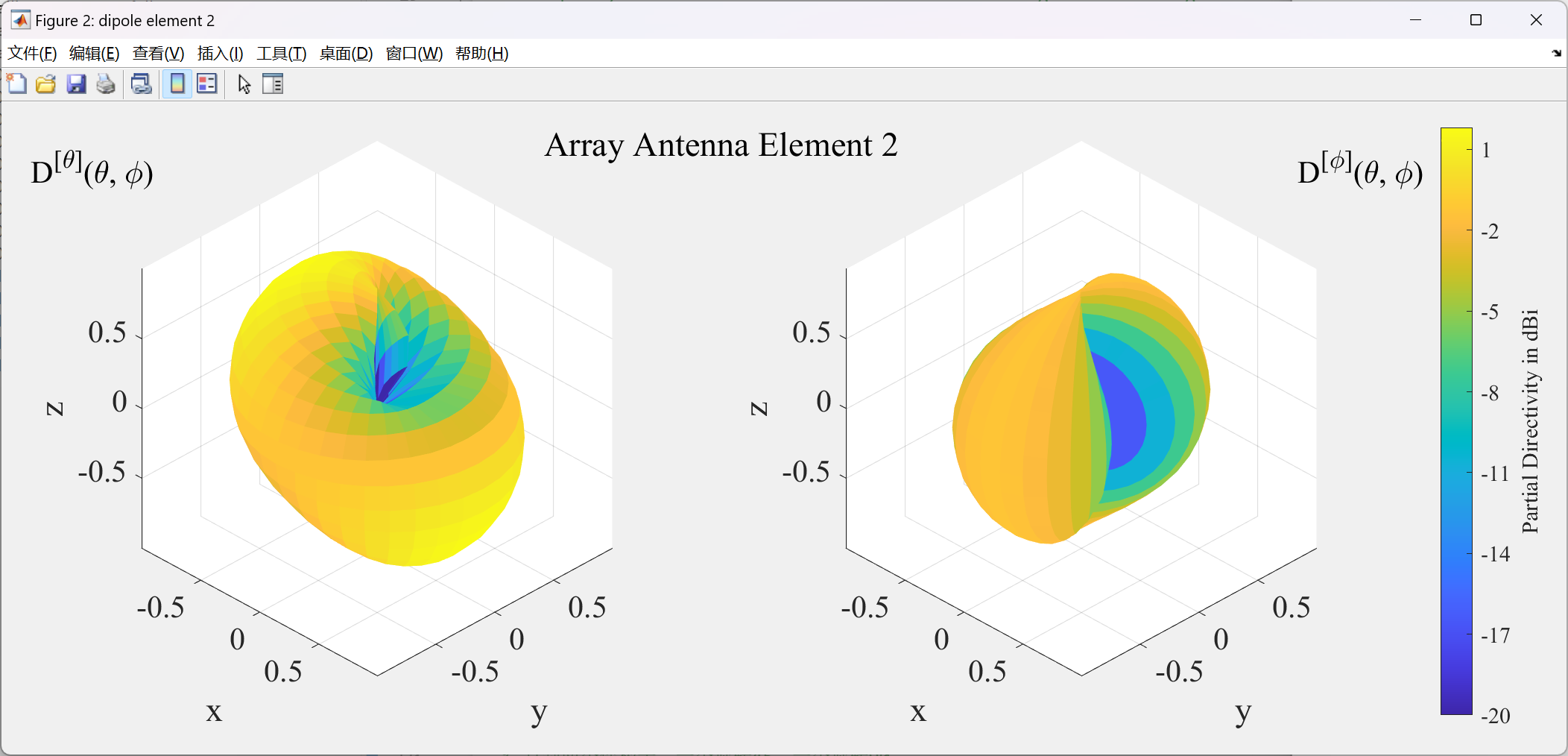
这是由于坐标系没有旋转造成的
那么为了处理这种情况,我们会利用笛卡尔坐标系下的旋转和映射,来计算field pattern
三.对于传播路程的研究
我们这里只考虑传播过程 θ \theta θ和 ϕ \phi ϕ的相对关系,而不考虑幅度的变化,因为这是path gain该思考的事情
由此,我们要引入琼斯向量的概念

琼斯向量的意义是,当我们把Field pattern看作一个琼斯向量,我们的传播路径M就可以看作各种各样对琼斯向量的变换操作这可以包括线性旋转,相位变化等

由此可以描述电磁波在传播过程中想法,相位的变化

四.极化失配

当传播而来的电场的方向不在一条直线上,就会存在损耗

五.传播结果
基于此,最后信道的传播路径参数是由下式得到的
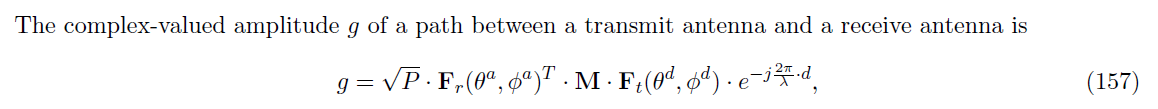
其中P是由path power计算得到的power gain,F是 filed pattern,M是传播电磁波发生的变化,相位是由路程长度得到的。而Fr和Ft的乘积,自带了极化失配的计算
六.QuaDRiGa Tutorial分析
QuaDRiGa Tutorial给出的场景大致如下
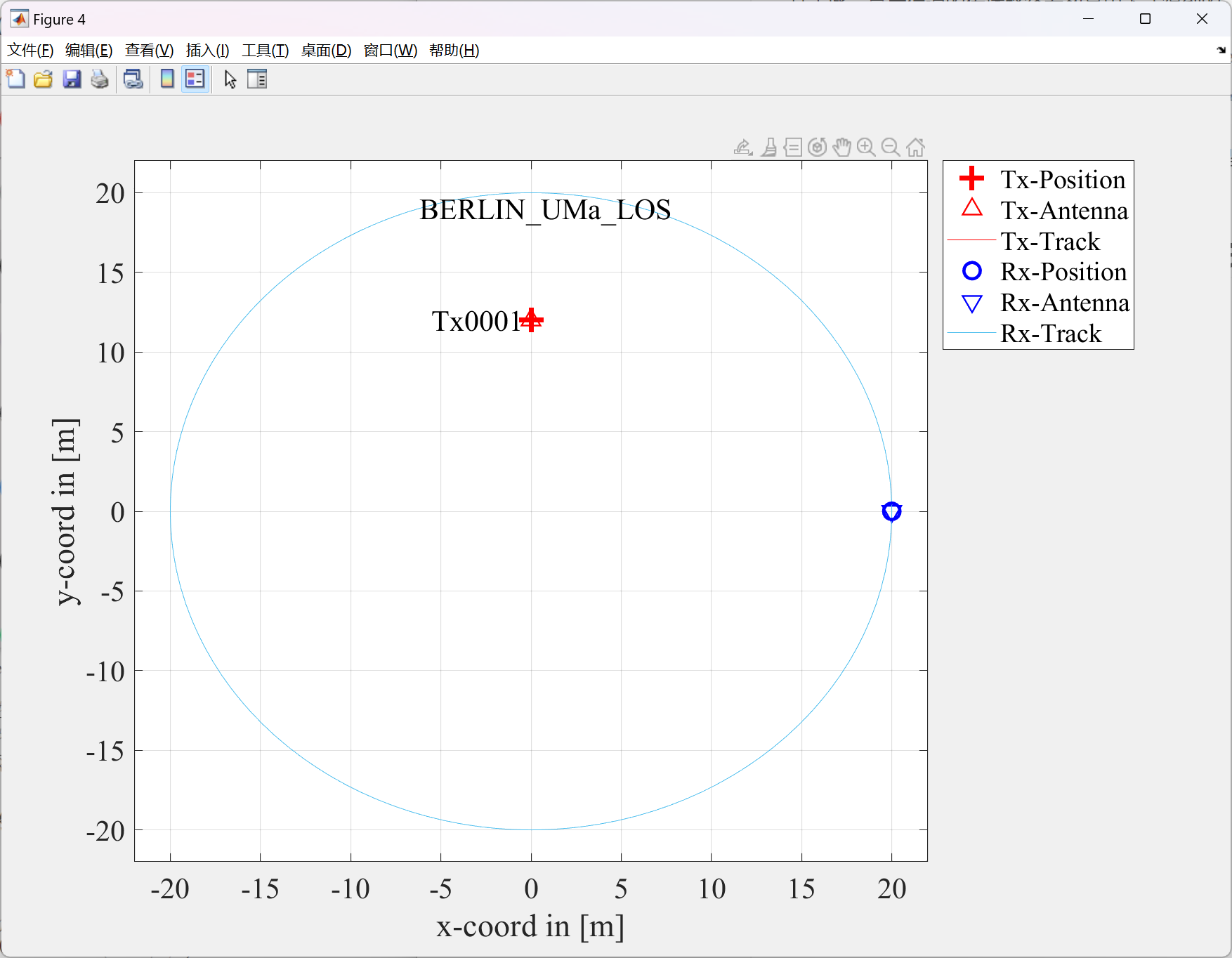
在中心红色Tx处,有一个半波偶极子极化天线,在蓝色车上有一个半波偶极子极化天线,他绕着Tx旋转,来表示两者之间的角度变化
TXV-RXV
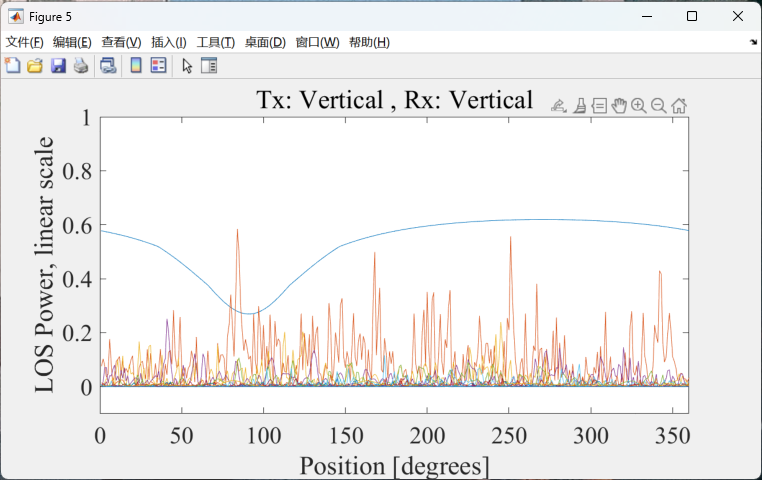
结果如下图,这是由于半波偶极子在正下方的field pattern几乎没有,因此会有一个突然的下降

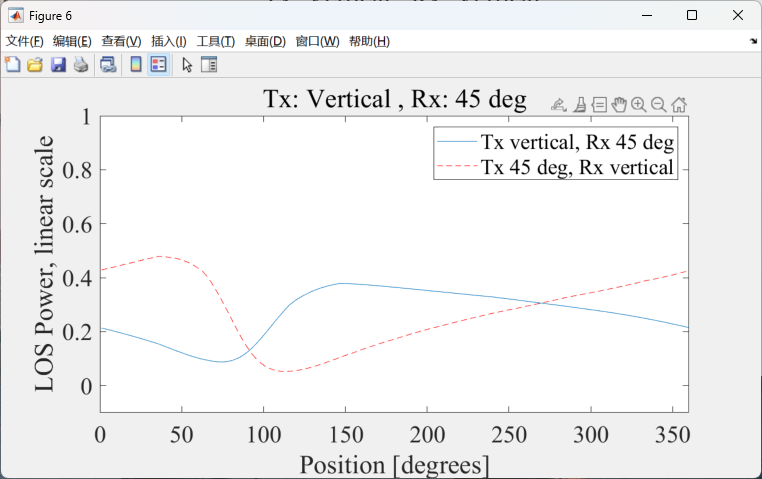
TX45-RXV和 TXV-RX45
存在固定的极化失配,且在下方最大
TX45-RX45
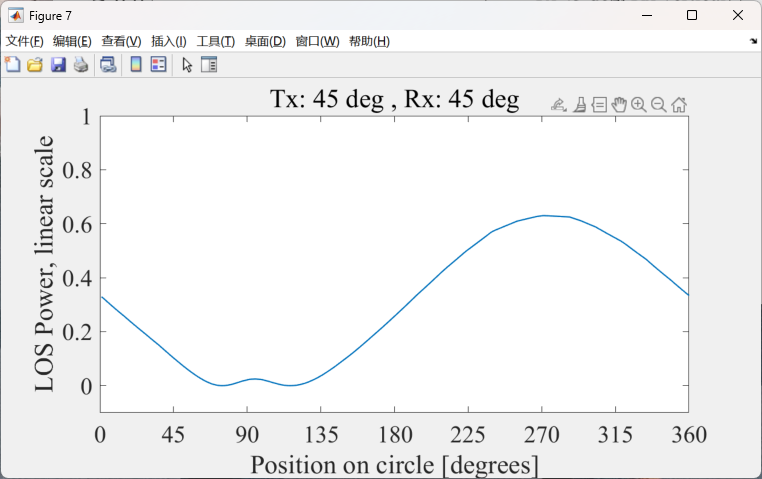
请注意TX是绕x旋转45,RX绕y旋转45
自己用手比划一下,在90°,两天线垂直,在270°,两天线平行
因此在90几乎为0,在270最大
TX90-RX0,45,90
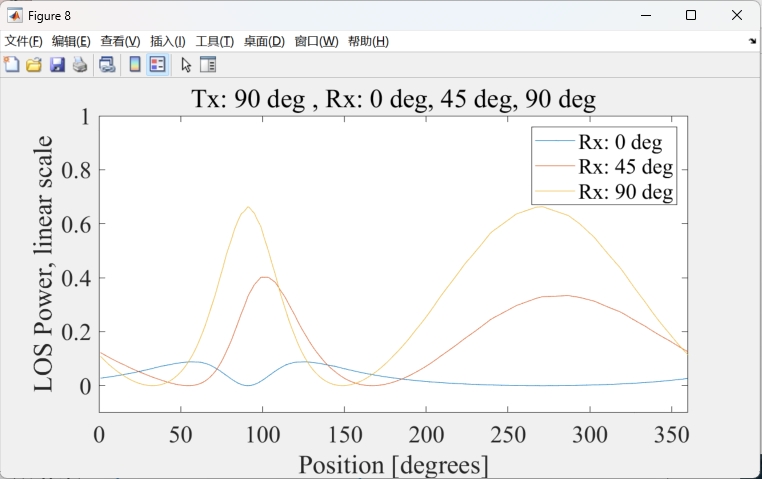
请思考,90和270时,对于90°天线,他们都平行,因此近似于一三角函数
对于0°天线,他们始终垂直
这就是所谓的极化失配,因为电场方向和偶极子天线的方向是平行的,他们之间的夹角就是极化失配的损耗
![[Linux]-Crontab定时任务](https://img-blog.csdnimg.cn/8307c9f90b7c424ab8ec37fd0273676e.png#pic_center)
![[ 漏洞挖掘基础篇六 ] 漏洞挖掘之越权漏洞挖掘](https://img-blog.csdnimg.cn/36a1dbb8cca742dbb8683526e1b392c9.png)