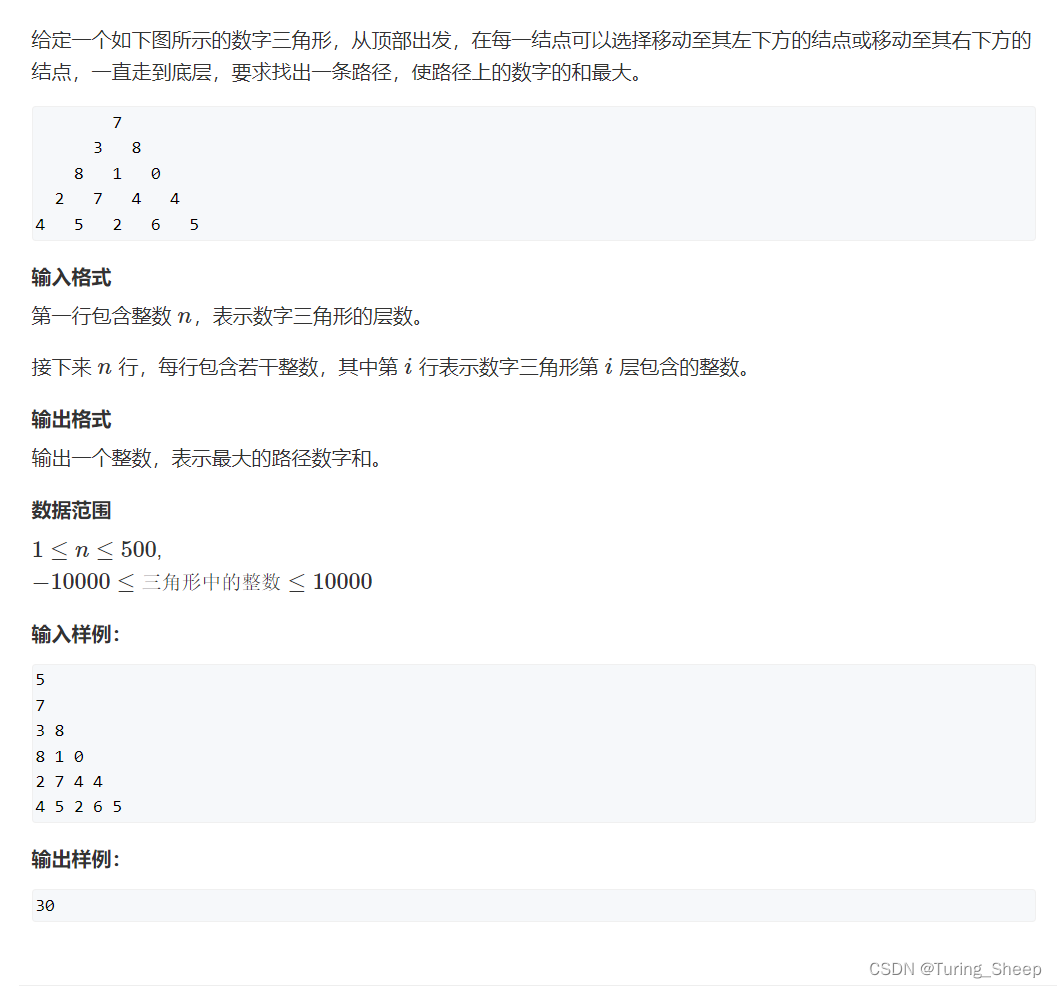
一、题目描述

二、题目分析

1、问题分析

这道题给我们的第一眼感觉就是情况太多了，太复杂了。而这种情况下，我们往往需要缩小问题的规模，从小问题看起，看清这道题的规律。

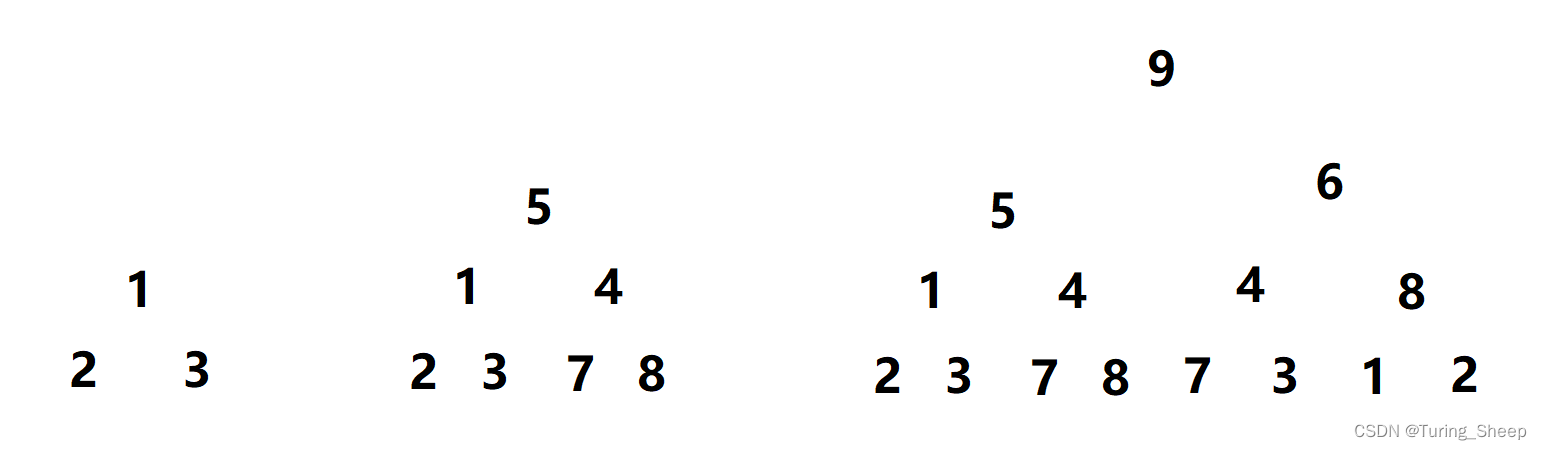
我们看上面图片中最左边的图，我们发现这个规模的问题就非常好解决了，我们只需要对比从1到2和从1到3谁大即可。

然后我们看中间的图片，我们的从最上方的5到下一层的方式有两种，要么到1，要么到4。在这个过程中，我们发现当它到1的时候，我们遇到了和左边相同的问题，也就是说左面的是中间的子问题。这个规律在第三个图中依然满足。

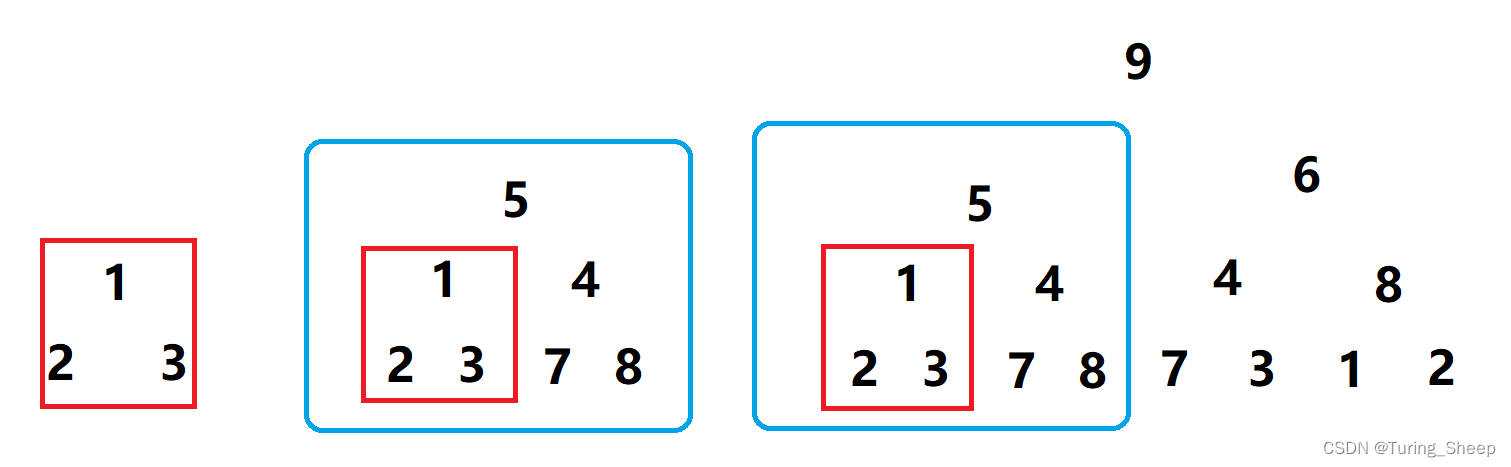
那么当一个问题满足这个特点的时候，我们就说这个问题具备重叠子问题的性质。

同时在我们每次选择过后，问题的规模都会减小，但是我们依旧需要做出最优选择，此时说明这个问题具备最优子结构。

另外，我们解决大规模问题的时候，我们的小问题的最优解是没有发生变化的。而这种性质称作无后效性。

当一道题的问题满足上述三个性质的时候，我们通常可以使用动态规划的方式去解决。

2、思路分析

既然要用动态规划的方式来解决这道题的话，我们就需要考虑两个问题：状态转移方程的书写、循环的设计。

（1）状态转移方程

状态转移方程的作用就是利用子问题去解决问题，或者说是，将一个大规模问题转化为小规模问题。
而转移方程的书写我们还需要思考两个问题：
1、状态表示
2、状态转移

状态表示

我们发现，我们一个问题的规模其实就取决于最高点的那个坐标，所以我们将最高点的坐标作为状态的表示。

$f(i,j)$指的是，我们坐标为$(i,j)$的点向下走到底的时候，所能够经过路线的点的和的最大值。

状态转移

我们根据我们刚刚举的例子，我们发现减小问题规模的关键就是在向左下和向右下走做出一个决定，然后在二者之间取出一个最大值。但是我们需要注意的是，我们向下走其实坐标值是在增大的。

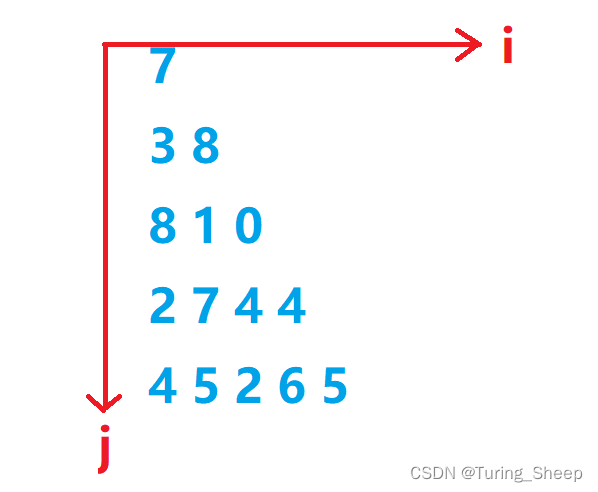
如下：

$$f(i,j)=max\{\begin{array}{l}f(i+1,j+1)+w[i][j]\\ f(i+1,j)+w[i][j]\end{array}$$

（2）循环的设计

我们相同规模的问题在同一行，所以我们最外层循坏一定是行数，那么第二层循环就是列数。

我们一定是先从小规模的问题开始枚举，而最小规模的问题对应的是最大的下标。因此，我们只需要将第一层逆置过来即可，第二层是否逆置无所谓。

三、代码实现

#include<iostream>
using namespace std;
const int N=1e3+10;
int dp[N][N],a[N][N];
int n,m;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        scanf("%d",&a[i][j]);
    }
    for(int i=n;i>=1;i--)
    {
        for(int j=1;j<=n;j++)
        {
            dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];
        }
    }
    cout<<dp[1][1]<<endl;
    return 0;
}